A uniform thin rod of mass m and length R is placed normally on surface of earth as shown. The mass of earth is M and its radius is R. If the magnitude of gravitational force exerted by earth on the rod is ηGMm12R2 then η is
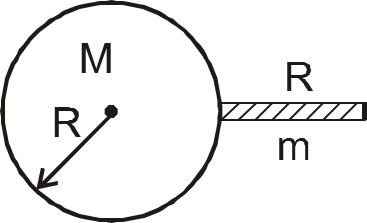

F=∫2RRGM(±R)dxx2=GMm2R2
Topper's Solved these Questions
Similar Questions
A uniform thin rod of mass m and length R is placed normally on surface of earth as shown. The mass of earth is M and its radius R. Then the magnitude of gravitational force exerted by earth on the rod is

View SolutionIf M is the mass of the earth and R its radius, the radio of the gravitational acceleration and the gravitational constant is
View Solution
Knowledge Check
If M is the mass of the earth and R its radius, then ratio of the gravitational acceleration and the gravitational constant is
AR2EMEBMER2ECMER2EDMEREA point mass m is placed inside a spherical shell of radius R and mass M at a distance R2 form the centre of the shell. The gravitational force exerted by the shell on the point mass is
AGMmR2B2GMmR2CzeroD4MmR2
Gravitational potential energy of body of mass m at a height of h above the surface of earth (M = mass of earth , R = radius of earth) is
View SolutionA uniform rod of mass m and length l is lying on a smooth table. An impulse J acts on the rod momentarily as shown in figure at point R. Just after that:
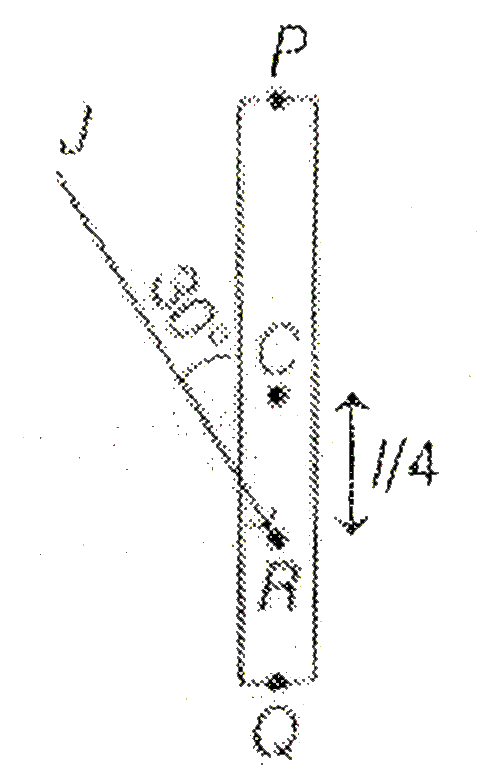
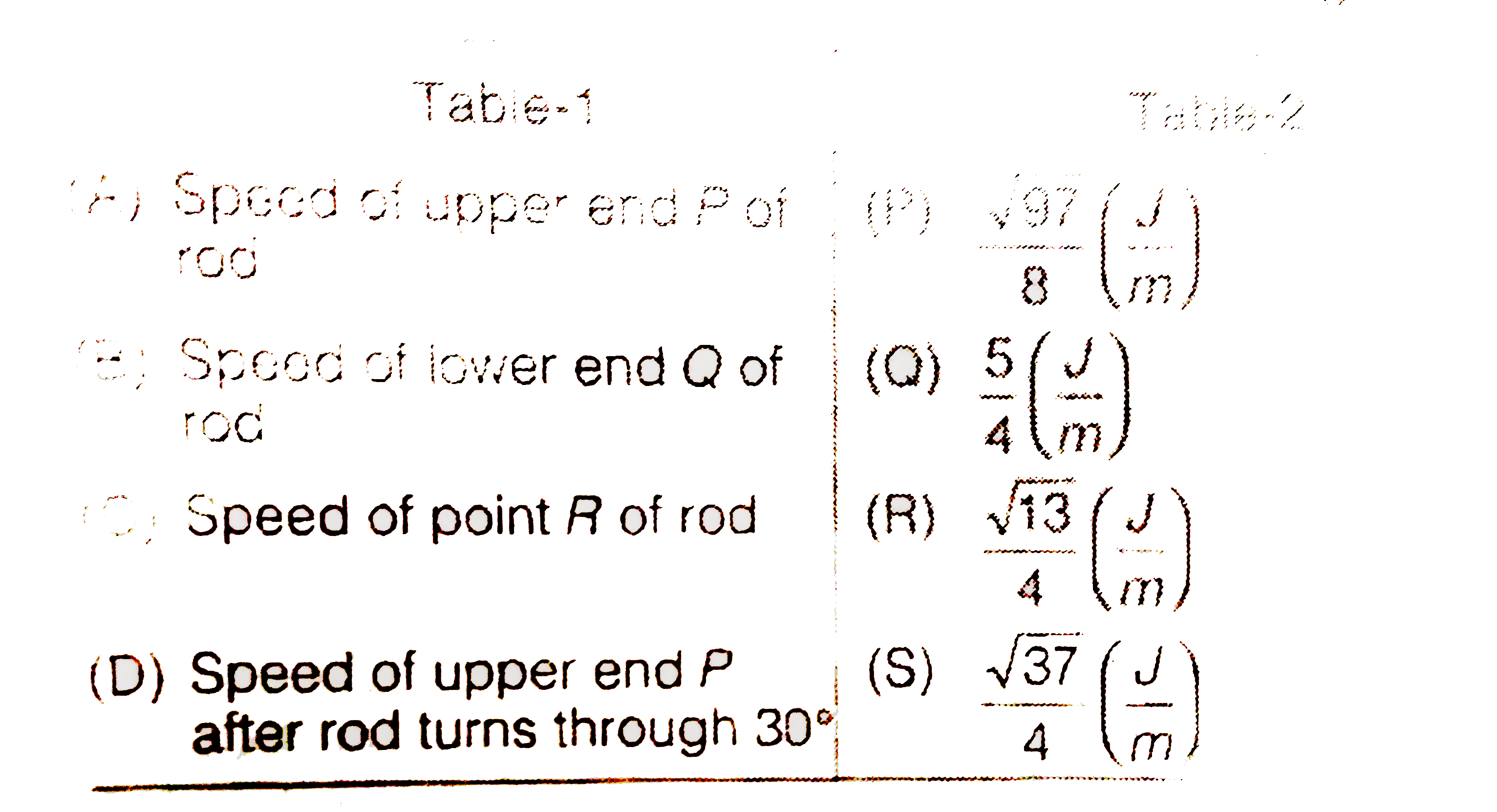
View SolutionA man weighs 'W' on the surface of the earth and his weight at a height 'R' from surface of the earth is (R is Radius of the earth )
View SolutionA body of mass m is placed on the earth's surface . It is taken from the earth's surface to a height h = 3 R where R is the radius of the earth. The change in gravitational potential energy of the body is
View SolutionIf body of mass mhas to be taken from the surface to the earth to a height h=4R, then the amount of energy required is (R = radius of the earth)
View SolutionA uniform solid sphere of mass m and radius r is suspended symmetrically by a uniform thin spherical shell of radius 2r and mass m.
View Solution

