Consider a hypothetical solar system, which has two identical massive suns each of mass M and radius r, seperated by a seperation of 2√3R (centre to centre). (R>>r). These suns are always at rest. There is only one planet in this solar system having mass m. This planet is revolving in circular orbit of radius R such that centre of the orbit lies at the mid point of the line joining the centres of the sun and plane of the orbit is perpendicular to the line joining the centres of the sun. Whole situation is shown in the figure.
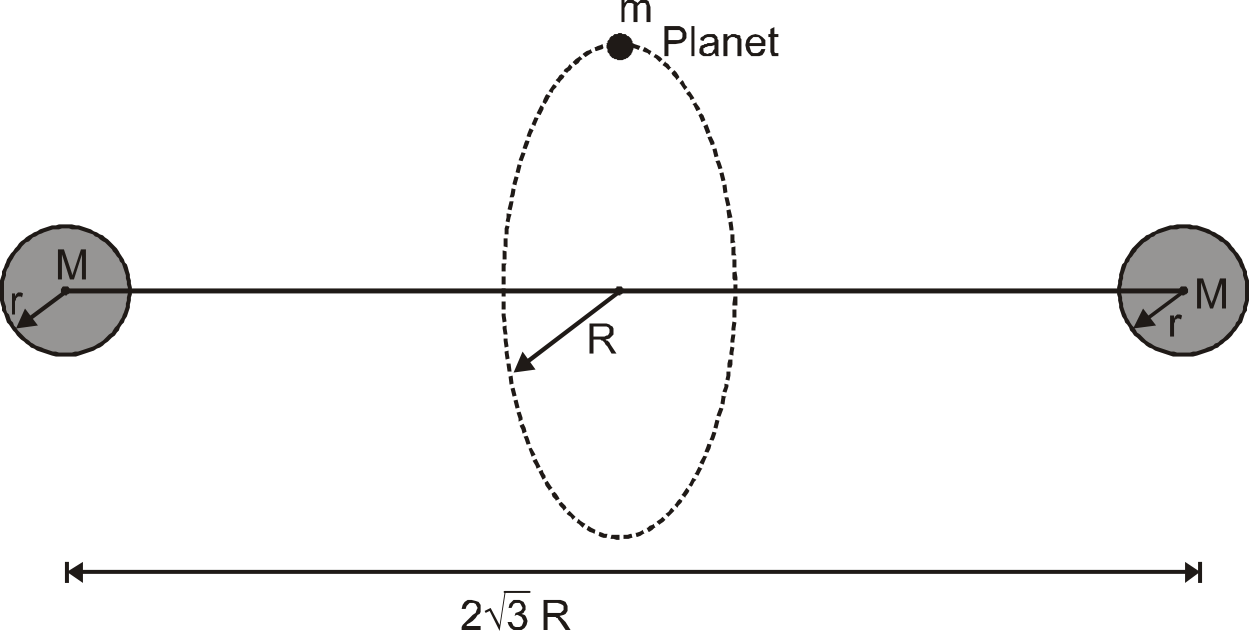
Q. Speed of the planet is
√GM8R
√GM4R
√GM2R
√GM3R

Fnet=2(GMm4R2)cos60∘=GMm4R2
Fnet=GMm4R2=mv2R⇒v=√GM4R=12√GMR
T=2πRv=4πR3/2√GM
Average force on planet half revolution
Favg=2mvT/2=4mvT=4mv2πRv=2mv2πR=GMm2πR2
Topper's Solved these Questions
Similar Questions
Consider a hypothetical solar system, which has two identical massive suns each of mass M and radius r, seperated by a seperation of 2√3R (centre to centre). (R gtgtgtr). These suns are always at rest. There is only one planet in this solar system having mass m. This planet is revolving in circular orbit of radius R such that centre of the orbit lies at the mid point of the line joining the centres of the sun and plane of the orbit is perpendicular to the line joining the centres of the sun. Whole situation is shown in the figure.
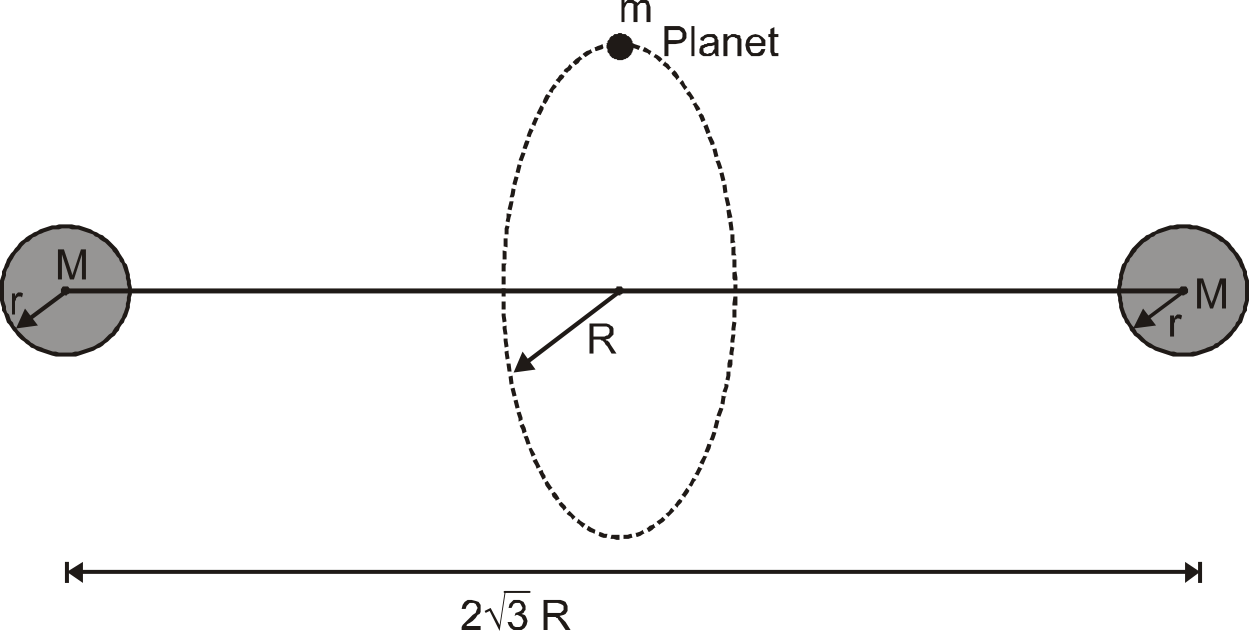
View SolutionConsider a hypothetical solar system, which has two identical massive suns each of mass M and radius r, seperated by a seperation of 2√3R (centre to centre). (R gtgtgtr). These suns are always at rest. There is only one planet in this solar system having mass m. This planet is revolving in circular orbit of radius R such that centre of the orbit lies at the mid point of the line joining the centres of the sun and plane of the orbit is perpendicular to the line joining the centres of the sun. Whole situation is shown in the figure.

Q. Average force on the planet in half revolution is
View Solution
Knowledge Check
Two spheres each of mass M and radius R are separated by a distance of r. The gravitational potential at the midpoint of the line joining the centres of the spheres is
A−GMrB−2GMrC−GM2rD−4GMrTwo identical spheres each of mass M and Radius R are separated by a distance 10R. The gravitational force on mass m placed at the midpoint of the line joining the centres of the spheres is
AzeroB2GMm25R2CGMm25R2DGMm100R2
An electron moving in a circular orbit of radius R with frequency f. The magnetic field at the centre of the orbit is
View SolutionA satellite of mass m moving around the earth of mass m in a circular orbit of radius R has angular momentum L. The rate of the area swept by the line joining the centre of the earth and satellite is
View SolutionTwo spheres each of mass M and radius R are separated by a distance of r. The gravitational potential at the midpoint of the line joining the centres of the spheres is
View SolutionFor a uniform ring of mass M and radius R at its centre
View SolutionA satellite of mass m is in a circular orbit of radius r round the Earth. Calculate its angular momentum with respect to the centre of the orbit in terms of the mass M of the Earth and G.
View SolutionA sayellite of mass m revolves in a circular orbit of radius R a round a planet of mass M. Its total energy E is :-
View Solution

