A ray incident on a droplet of water from air at an angle of incidence 30∘ undergoes two reflections and emerges. If the deviation suffered by the ray is minimum then the requried refractive index of the drop μ=√x. Find the value of x.
The correct Answer is:7
To solve the problem, we need to determine the value of x such that the refractive index μ of the water droplet is given by μ=√x and the deviation suffered by the ray is minimized.
1. Identify the Given Values:
- Angle of incidence i=30∘
- The ray undergoes two reflections inside the droplet.
2. Understanding the Refraction and Reflection:
- When the ray enters the droplet, it refracts at the air-water interface.
- It then reflects off the inner surface of the droplet and refracts again when it exits back into the air.
3. Using Snell's Law:
- At the first interface (air to water), Snell's law states:
sini=μsinr
- Here, r is the angle of refraction.
4. Calculating the Deviation:
- The deviation δ for the ray after two reflections can be expressed as:
δ=(i−r)+(i−r)+(π−2r)+(π−2r)=2i−2r+2(π−2r)
- Simplifying this gives:
δ=2i−2r+2π−4r=2i+2π−6r
5. Minimizing the Deviation:
- To minimize the deviation, we take the derivative of δ with respect to r and set it to zero:
dδdr=−6=0
- This implies that for minimum deviation, we need to find the relationship between i and r.
6. Finding the Relationship:
- From the condition for minimum deviation:
drdi=13
- Using Snell's law:
sini=μsinr
- Differentiating gives:
cosidi=μcosrdr
7. Substituting Values:
- Substitute i=30∘ and sin30∘=12:
sin30∘=μsinr
- Thus:
12=μsinr
8. Using the Relationship:
- From the earlier derived relationship:
μ2=1−sin2rcos2r
- Substitute sinr=12μ into this equation.
9. Final Calculation:
- After substituting and simplifying, we find:
μ2=7
- Therefore, x=7.
Conclusion:
The value of x is 7.
- Angle of incidence i=30∘
- The ray undergoes two reflections inside the droplet.
- When the ray enters the droplet, it refracts at the air-water interface.
- It then reflects off the inner surface of the droplet and refracts again when it exits back into the air.
- At the first interface (air to water), Snell's law states:
sini=μsinr
- Here, r is the angle of refraction.
- The deviation δ for the ray after two reflections can be expressed as:
δ=(i−r)+(i−r)+(π−2r)+(π−2r)=2i−2r+2(π−2r)
- Simplifying this gives:
δ=2i−2r+2π−4r=2i+2π−6r
- To minimize the deviation, we take the derivative of δ with respect to r and set it to zero:
dδdr=−6=0
- This implies that for minimum deviation, we need to find the relationship between i and r.
- From the condition for minimum deviation:
drdi=13
- Using Snell's law:
sini=μsinr
- Differentiating gives:
cosidi=μcosrdr
- Substitute i=30∘ and sin30∘=12:
sin30∘=μsinr
- Thus:
12=μsinr
- From the earlier derived relationship:
μ2=1−sin2rcos2r
- Substitute sinr=12μ into this equation.
- After substituting and simplifying, we find:
μ2=7
- Therefore, x=7.
The value of x is 7.
Similar Questions
A ray incident on the droplet of water at an angle of incidence i undergoes two reflections (not total) and emerges. If the deviation suffered by the ray within the drop is minimum and the refractive index of the droplet be μ, then show that cosi=√(u2−1)8.
View SolutionFind the angle of deviation suffered by the light ray shown in figure. The refractive index μ=2.0 for the prism material.
View Solution
A ray is incident on a sphere of refractive index √2 as shown in figure. Angle of refraction of the ray inside sphere is 30∘ if total deviation suffered by the ray is 30x0, then find x.
View SolutionA ray of light is incident on a rectangular plate at an angle of incidence 60∘. The light ray suffers a deviation which is 25% of the angle of incidence. The refractive index of the glass will be
View SolutionA ray of light incident at an angle of incidence 48∘ on a prism of refracting angle 60∘ suffers minimum deviation. Calculate the angle of minimum deviation.
View SolutionA light ray is incident on a transparent sphere of index = √2 , at an angle of incidence =45∘ , What is the deviation of a tiny fraction of the ray, which enters the sphere, undergoes two internal reflections and then refracts out into air?
View SolutionA light ray is incident on a glass sphere of reflective index μ=√3 at an angle of incidence 60∘ as shown in Fig. Find the angles r, r′ e and the total deviation after two refractions.
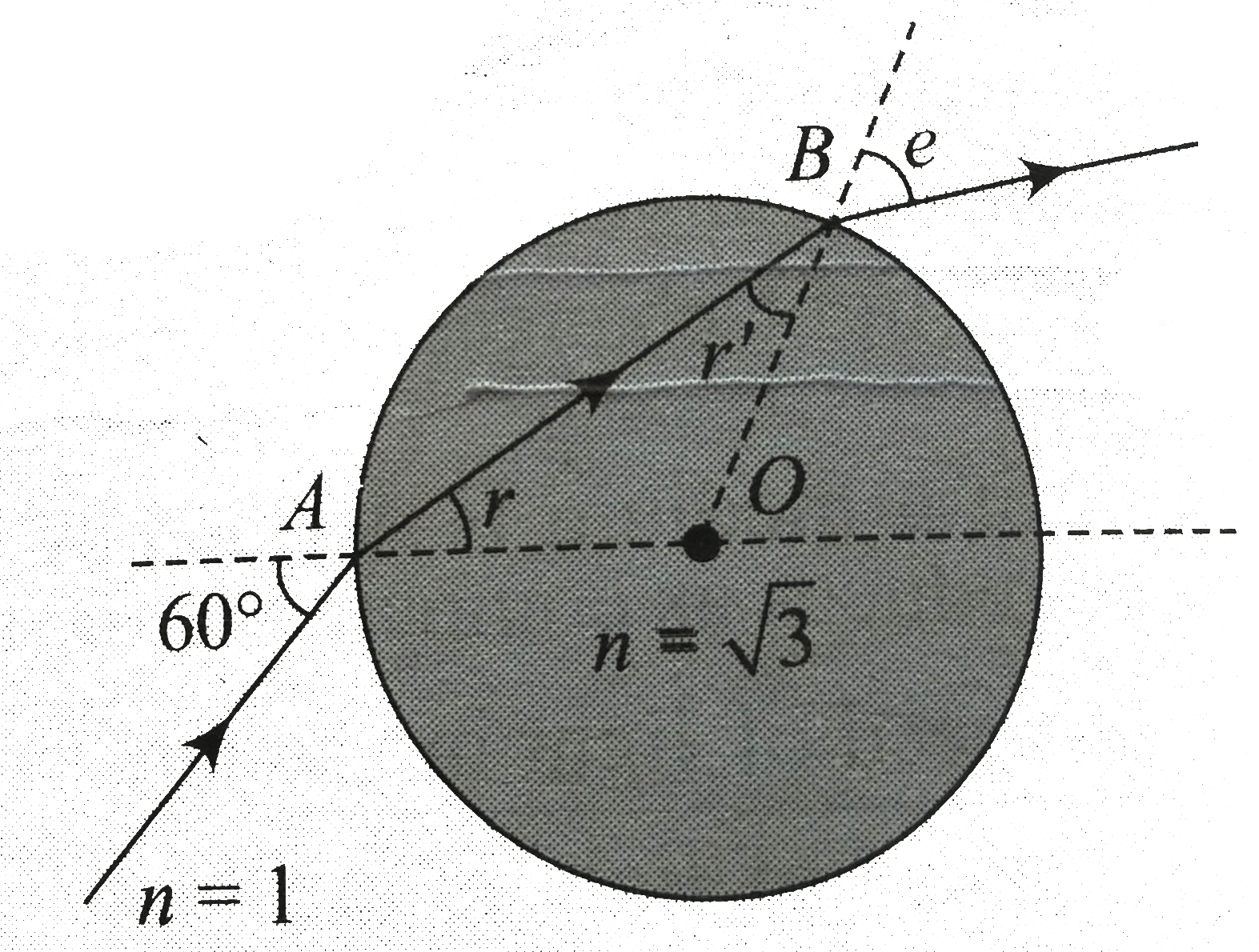
View SolutionA light ray is incident on a transparent slab of refractive index μ=√2 at an angle of incidence π/4. Find the ratio of the lateral displacement suffered by the light ray to the maximum value which it could have suffered.
View SolutionA ray of light is incident at an angle of 60∘ on one face of a prism which has refracting angle of 30∘ . The ray emerging out of the prism makes an angle of 30∘ with the incident ray. If the refractive index of the material of the prism is μ=√a , find the value of a .
View SolutionA light ray of angles of incidence 40∘ emerged from the prism in minimum deviation position. Then what is the angle of incidence on the second surface ?
View Solution
