
A ray is incident on a sphere of refractive index √2 as shown in figure. Angle of refraction of the ray inside sphere is 30∘ if total deviation suffered by the ray is 30x0, then find x.
The correct Answer is:5

sinisinr=√2⇒i=45∘
total deviation
=(45∘−30∘)+180∘−2(30∘)+(45∘−30∘)
=30∘+120∘
=150∘=30x
x=5
Similar Questions
A ray of light is incident on a glass sphere of refractive index 3/2. What should be the angle of incidence so that the ray which enters the sphere does not come out of the sphere ?
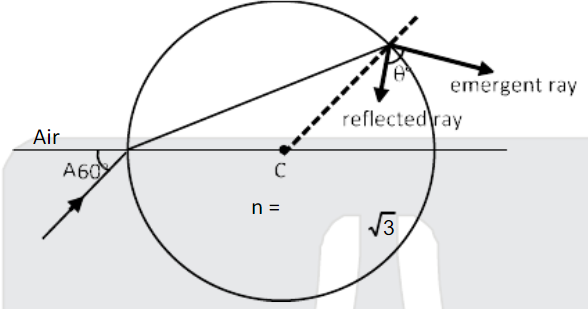
View SolutionLight incidence on a sphere of refractive index √3 placed in a air as shown in Figure. Find the angle (θ)in degree between emergent ray and reflected ray.
View SolutionA light ray is incident on a transparent slab of refractive index μ=√2 at an angle of incidence π/4. Find the ratio of the lateral displacement suffered by the light ray to the maximum value which it could have suffered.
View SolutionA light ray is incident on a glass sphere of reflective index μ=√3 at an angle of incidence 60∘ as shown in Fig. Find the angles r, r′ e and the total deviation after two refractions.
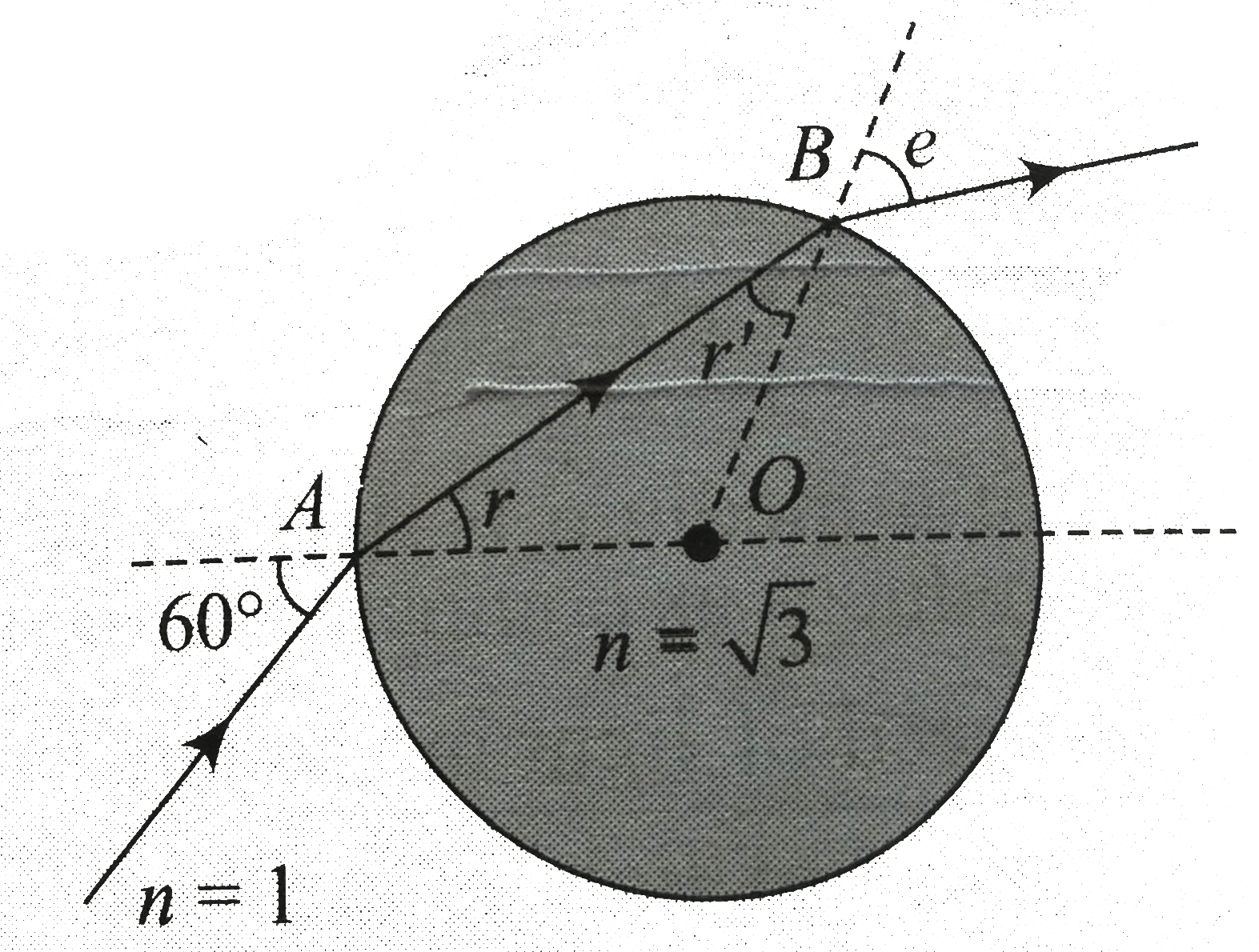
View SolutionA light ray is normally incident onone face of equilateral glass prism of refractive index √2. The deviation of light ray is
View SolutionA ray of light enters a spherical drop of water of refractive index p as shown in the figure.
An expression of the angle between incidence ray and emergent ray (angle of deviation) as shown in the figure is

View SolutionA ray of light is incident on the surface of a glass plate of refractive index √3 at the polarising angle . The angle of incidence and angle of refraction of the ray is
View SolutionA ray of light is incident on the surface of a sphere of refractive index √72 other half of sphere is silvered. After refraction it is reflected and then refracted out of sphere again such that the total deviation is minimum then total deviation of the ray will be (sin410−√37)

View SolutionA light ray is incident on a glass sphere at an angle of incidence 60∘ as shown. Find the angles r,r1,e and the total deviation after two refractions.

View SolutionA ray of light is incident on a prism ABC of refractive index √3 as shown in the figure.
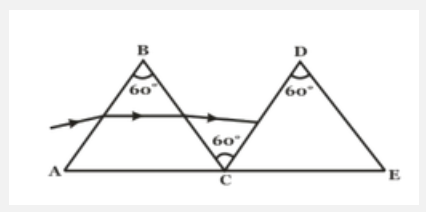
The angle by which the second identical prism must be rotated so that the final ray suffers net minimum deviation is
View Solution
