A light ray is incident on a transparent sphere of index = √2 , at an angle of incidence =45∘ , What is the deviation of a tiny fraction of the ray, which enters the sphere, undergoes two internal reflections and then refracts out into air?
270∘
240∘
120∘
180∘
The correct Answer is:A
To solve the problem, we will follow these steps:
Step 1: Determine the angle of refraction at the first interface
Given:
- Refractive index of the sphere, μ=√2
- Angle of incidence, i=45∘
- Refractive index of air, μ1=1
Using Snell's law:
μ1sin(i)=μ2sin(r)
Substituting the values:
1⋅sin(45∘)=√2⋅sin(r)
sin(r)=sin(45∘)√2=√22√2=12
Thus,
r=30∘
Step 2: Analyze the internal reflections
After refraction, the ray enters the sphere and will undergo two internal reflections. The angle of incidence for each reflection will be equal to the angle of refraction from the previous interface.
1. First internal reflection: The angle of incidence is 30∘, so the angle of reflection is also 30∘.
2. Second internal reflection: The angle of incidence remains 30∘, leading to another reflection at 30∘.
Step 3: Determine the angle of refraction at the exit interface
After the second reflection, the ray exits the sphere. The angle of incidence at the exit interface is again 30∘.
Using Snell's law again:
√2⋅sin(30∘)=1⋅sin(r′)
sin(r′)=√2⋅12=√22
Thus,
r′=45∘
Step 4: Calculate the total deviation
Now, we need to calculate the total deviation caused by the two refractions and two reflections.
1. Deviation due to refraction: Each refraction causes a deviation of 15∘ (since 45∘−30∘=15∘). Thus, for two refractions:
Total deviation due to refraction=2×15∘=30∘
2. Deviation due to reflection: Each reflection also contributes to the deviation. The deviation caused by each reflection is 30∘ (the angle of incidence). Thus, for two reflections:
Total deviation due to reflection=2×30∘=60∘
Step 5: Combine the deviations
The net deviation D is given by:
D=Deviation due to refraction+Deviation due to reflection
D=30∘+60∘=90∘
Final Result
The total deviation of the light ray after undergoing two internal reflections and then refracting out into air is 90∘.
---
Given:
- Refractive index of the sphere, μ=√2
- Angle of incidence, i=45∘
- Refractive index of air, μ1=1
μ1sin(i)=μ2sin(r)
Substituting the values:
1⋅sin(45∘)=√2⋅sin(r)
sin(r)=sin(45∘)√2=√22√2=12
Thus,
r=30∘
After refraction, the ray enters the sphere and will undergo two internal reflections. The angle of incidence for each reflection will be equal to the angle of refraction from the previous interface.
2. Second internal reflection: The angle of incidence remains 30∘, leading to another reflection at 30∘.
After the second reflection, the ray exits the sphere. The angle of incidence at the exit interface is again 30∘.
√2⋅sin(30∘)=1⋅sin(r′)
sin(r′)=√2⋅12=√22
Thus,
r′=45∘
Now, we need to calculate the total deviation caused by the two refractions and two reflections.
Total deviation due to refraction=2×15∘=30∘
Total deviation due to reflection=2×30∘=60∘
The net deviation D is given by:
D=Deviation due to refraction+Deviation due to reflection
D=30∘+60∘=90∘
The total deviation of the light ray after undergoing two internal reflections and then refracting out into air is 90∘.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE-2
44 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE-3
12 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE - 05 (B) (ASSERTION & REASON )
9 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
Similar Questions
A light ray is incident on a glass sphere at an angle of incidence 60∘ as shown. Find the angles r,r1,e and the total deviation after two refractions.

View SolutionA light ray is incident on a glass sphere of reflective index μ=√3 at an angle of incidence 60∘ as shown in Fig. Find the angles r, r′ e and the total deviation after two refractions.
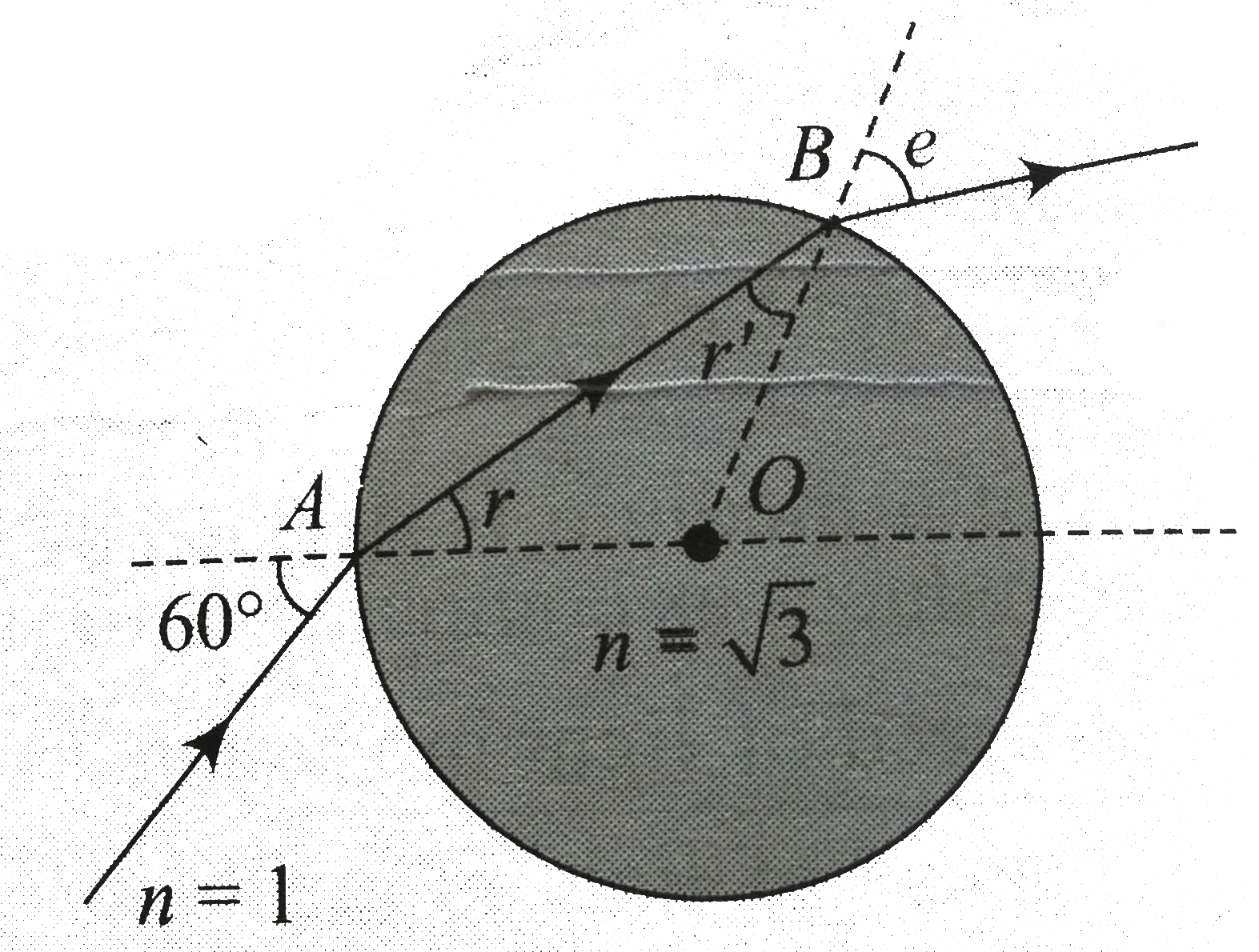
View Solution
Knowledge Check
A ray of light strikes a transparent rectangular slab of refractive index √2 at an angle of incidence of 45∘. The angle betweent the reflected and refracted rays is
A75∘B90∘C105∘D120∘
A light ray is incident on a transparent slab of refractive index μ=√2 at an angle of incidence π/4. Find the ratio of the lateral displacement suffered by the light ray to the maximum value which it could have suffered.
View SolutionLight ray is incident on a prism of angle A=60∘ are refractive index μ=√2. The angle of incidence which the emergent rays grazes the surface is given
View SolutionA ray of light is incident on the surface of a glass plate of refractive index √3 at the polarising angle . The angle of incidence and angle of refraction of the ray is
View SolutionA ray of light is incident on a glass sphere of refractive index 3/2. What should be the angle of incidence so that the ray which enters the sphere does not come out of the sphere ?
View SolutionA ray of light is incident on a rectangular plate at an angle of incidence 60∘. The light ray suffers a deviation which is 25% of the angle of incidence. The refractive index of the glass will be
View SolutionA ray of light is incident on one face of a transparent slab of thickness 15 cm. The angle of incidence is 60∘. If the lateral displacement of the ray on emerging from the parallel plane is 5√3 cm, the refractive index of the material of the slab is
View SolutionA horizontal ray of light is incident on a solid glass sphere of radius R and refractive index μ . What is net deviation of the beam when it emerged from the other side of the sphere?
View Solution
