Refractive index of water with respect to air is √2. Alight ray is incident on the surface at an angle 30° travelling through water. The deviation of light ray is
30∘
120∘
`15^@`
60∘
The correct Answer is:D
d=i−r and μ=sinisinr
Related Playlists
- BOOK - NARAYNACHAPTER - RAY OPTICS AND OPTICAL INSTRAUMENTS EXERCISE - EXERCISE-2 (H.W)(REFRACTION THROUGH SPHERICAL SURFACES)5videos
RAY OPTICS AND OPTICAL INSTRAUMENTS
- BOOK - NARAYNACHAPTER - RAY OPTICS AND OPTICAL INSTRAUMENTS EXERCISE - EXERCISE-2 (H.W)(LENSES & THEIR COMBINATIONS)23videos
RAY OPTICS AND OPTICAL INSTRAUMENTS
- BOOK - NARAYNACHAPTER - RAY OPTICS AND OPTICAL INSTRAUMENTS EXERCISE - EXERCISE-2 (H.W)(REFLECTION)15videos
RAY OPTICS AND OPTICAL INSTRAUMENTS
- BOOK - NARAYNACHAPTER - NUCLEI EXERCISE - ASSERTION & REASON5videos
NUCLEI
- BOOK - NARAYNACHAPTER - SEMI CONDUCTOR DEVICESEXERCISE - Level-II (H.W)36videos
SEMI CONDUCTOR DEVICES
Similar Questions
Refractive index of a rectangular glass slab is μ=√3. Alight ray incident at an angle 60° is displaced laterally through 2.5 cm. Distance travelled by light in the slab is
View SolutionThe refractive index of water relative to air is 5/3. A ray of light passing from water into air is incident at the interface at an angle of 32∘ with the normal. What angle does the refreacted ray make with the normal?
View SolutionA ray of light travelling inside a rectangular glass block of refractive index √2 is incident on the glass–air surface at an angle of incidence of 45∘. The refractive index of air is 1. Under these conditions the ray
View SolutionA ray of light travelling inside a rectangular glass block (μ=√2) is incident on the glass-air surface at an angle of incidence of 45∘. The refractive index of air is 1. The ray will
View SolutionA ray of light is incident on the surface of plate of glass of refractive index 1.5 at the polarising angle. The angle of refraction of the ray will be
View SolutionThere is an equilateral prism of material of refractive index 1.5. Light ray is incident normally on its surface. What will be the angle of deviation of ray ?
View SolutionA ray of light travelling inside a rectangular glass block of refractive index√2is incident on the glass-air surface at an angle of incidence of 45∘. The refractive index of air is one. Under these conditions the ray will
View SolutionA ray of light travelling inside a rectangular glass of block of refractive indx ×√2 is incident on the glass air surface at an angle of incidence of 45∘ . the refractive index of air is 1 . The ray will
View SolutionThe figure given below shows a container C partially filled with water. There is a plane mirror M at the bottom of the container. A light ray AB incidents on the surface of water at angle of incidence 30∘. Copy and complete the ray diagram. Mark the ray emerging from the water surface. refractive index of water=43.
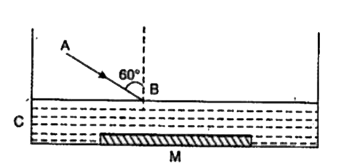 View Solution
View SolutionA film of oil of refractive index 1.20, lies on water of refractive index 1.33. A light ray is incident at 30∘ in the oil on the oil-water boundary. Calculate the angle of refraction in water.
View Solution


