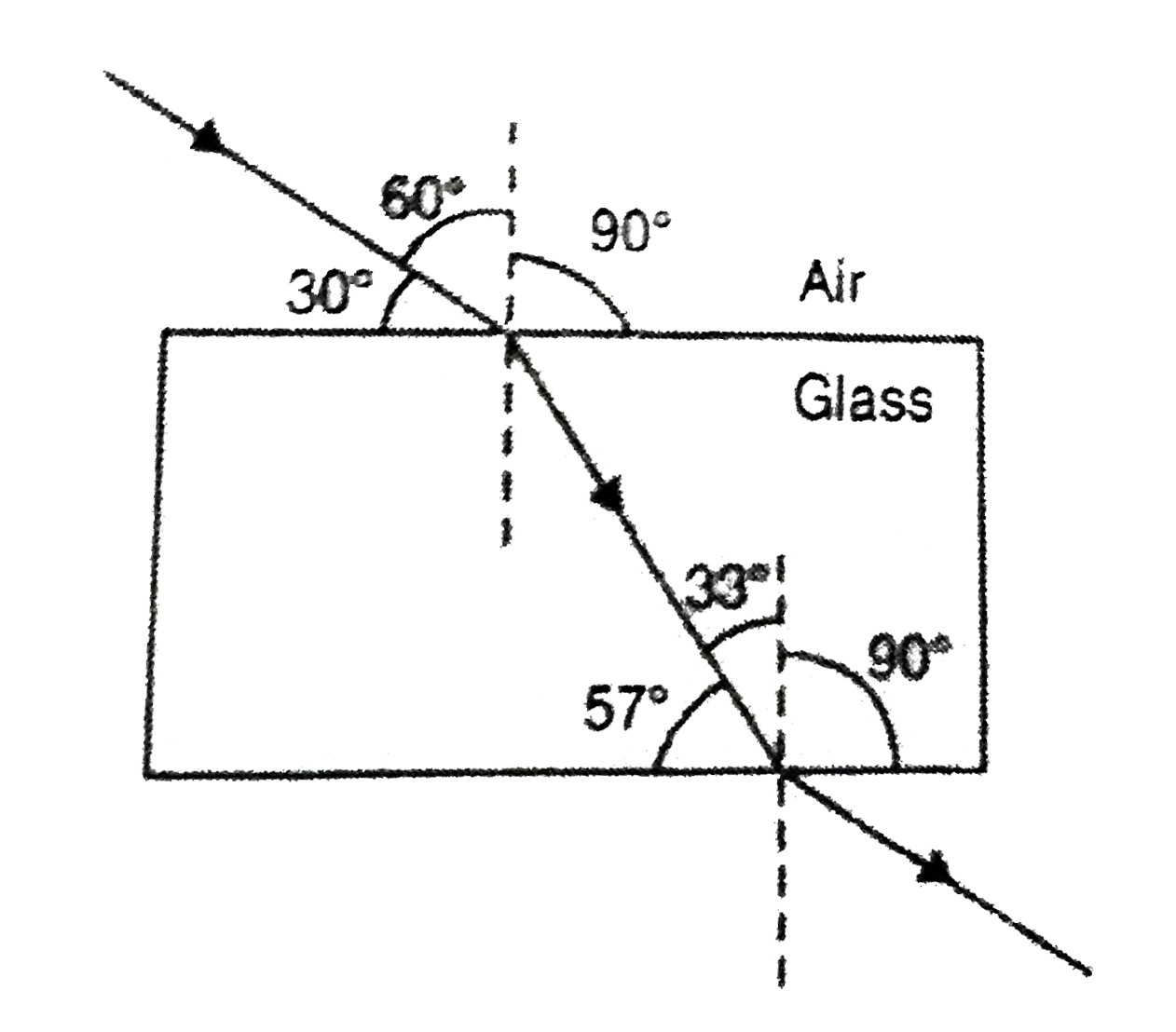
A ray of light is incident upon a parallel sided transparent slab of thickness 9 cm at an angle of incidence 60° • If the angle of refraction is 30°, the lateral displacement of the light ray is
cm
The correct Answer is:B
To solve the problem of finding the lateral displacement of a light ray passing through a parallel-sided transparent slab, we can follow these steps:
1. Identify Given Values:
- Thickness of the slab (t) = 9 cm
- Angle of incidence (i) = 60°
- Angle of refraction (r) = 30°
2. Understand the Formula for Lateral Displacement:
The formula to calculate the lateral displacement (x) of a light ray passing through a parallel-sided slab is given by:
x=t⋅sin(i−r)cos(r)
where:
- i is the angle of incidence,
- r is the angle of refraction,
- t is the thickness of the slab.
3. Calculate the Angle Difference:
First, we need to calculate i−r:
i−r=60°−30°=30°
4. Substitute Values into the Formula:
Now, we substitute the values into the formula:
x=9⋅sin(30°)cos(30°)
5. Calculate sin(30°) and cos(30°):
- sin(30°)=12
- cos(30°)=√32
6. Substitute the Trigonometric Values:
Now substitute these values back into the equation:
x=9⋅12√32=9⋅1√3
7. Simplify the Expression:
x=9√3=3√3 cm
8. Final Answer:
The lateral displacement of the light ray is:
x=3√3 cm
- Thickness of the slab (t) = 9 cm
- Angle of incidence (i) = 60°
- Angle of refraction (r) = 30°
The formula to calculate the lateral displacement (x) of a light ray passing through a parallel-sided slab is given by:
x=t⋅sin(i−r)cos(r)
where:
- i is the angle of incidence,
- r is the angle of refraction,
- t is the thickness of the slab.
First, we need to calculate i−r:
i−r=60°−30°=30°
Now, we substitute the values into the formula:
x=9⋅sin(30°)cos(30°)
- sin(30°)=12
- cos(30°)=√32
Now substitute these values back into the equation:
x=9⋅12√32=9⋅1√3
x=9√3=3√3 cm
The lateral displacement of the light ray is:
x=3√3 cm
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRAUMENTS Book:NARAYNAChapter:RAY OPTICS AND OPTICAL INSTRAUMENTS Exercise:EXERCISE-2 (H.W)(REFRACTION THROUGH SPHERICAL SURFACES)
Explore 5 Videos
- RAY OPTICS AND OPTICAL INSTRAUMENTS Book:NARAYNAChapter:RAY OPTICS AND OPTICAL INSTRAUMENTS Exercise:EXERCISE-2 (H.W)(LENSES & THEIR COMBINATIONS)
Explore 23 Videos
- RAY OPTICS AND OPTICAL INSTRAUMENTS Book:NARAYNAChapter:RAY OPTICS AND OPTICAL INSTRAUMENTS Exercise:EXERCISE-2 (H.W)(REFLECTION)
Explore 15 Videos
- NUCLEI Book:NARAYNAChapter:NUCLEI Exercise:ASSERTION & REASON
Explore 5 Videos
- SEMI CONDUCTOR DEVICESBook:NARAYNAChapter:SEMI CONDUCTOR DEVICESExercise:Level-II (H.W)
Explore 36 Videos
Similar Questions
A ray of light is incident on a transparent plate of a material of refractive index √3 at the polarising angle. Find the angle of refraction.
View SolutionLateral displacement of ray passing through a glass slab
A ray of light is incident on a parallel sided glass slab of refractive index n and thickness t as shown in Fig. 34-2. Find the lateral displacement of the ray as it passes through the slab.
View Solution
Knowledge Check
A ray of light is incident on a parallel slab of thickness t and refractive index n. If the angle of incidence θ is small, than the lateral displacement in the incident and emergent ray will be
Atθ(n−1)nBtθnCtθnn−1Dtθ(n+1)nA ray of light is incident on one face of a transparent glass slab of thickness 9cm at an angle of incidence 60∘. Lateral displacement of the ray on emerging from the opposite parallel face is 3√3cm. Refractive index of the material of slab is:
A√2B√32C√32D√3A ray of light is incident on a glass slab of thickness t, at an angle i,r is the angle of refraction in the glass slab. Distance travelled in the glass slab is
AtcosrBanrCtcosrDtsinr
A ray of light travelling in air is incident on the plane surface of a transparent medium. The angle of incidence is 45∘ and the angle of refraction is 30∘ . Find the refractive index of the medium .
View SolutionA light ray is incident on a plane glass slab of thickness ‘t’ at an angle of incidence ‘i’ as shown in the figure. If μ is the refractive index of glass. Then find time taken by the light ray to travel through the slab.
View SolutionLight passes through a glass slab with parallel sides and thickness t. If i and r the angles of incidence of refraction, the lateral displacement is
View SolutionA ray of light is incident on a glass slab of refractive index 1.5, making an angle of 40∘ with the surface. The angle of refraction in glass is
View SolutionA ray of light is incident on a parallel-sided glass slab as shown in the figure. The angle of refraction for this ray of light is likely to be :
View Solution