A ray of light from a rarer medium strikes a denser medium at angle of incidence 60°. The reflected and refracted rays are perpendicular to each other. The refractive index of denser medium and angle of deviation respectively are
√3,30∘
√2,45∘
√3,60∘
√2,30∘
The correct Answer is:A
To solve the problem step by step, we will determine the refractive index of the denser medium and the angle of deviation based on the given conditions.
Step 1: Understand the given information
- A ray of light strikes a denser medium from a rarer medium at an angle of incidence i=60∘.
- The reflected and refracted rays are perpendicular to each other.
Step 2: Identify the relationship between the angles
Since the reflected and refracted rays are perpendicular, we can denote the angle of refraction as r. The relationship can be expressed as:
i+r=90∘
This means:
r=90∘−i
Step 3: Calculate the angle of refraction
Substituting the value of i:
r=90∘−60∘=30∘
Step 4: Use Snell's Law to find the refractive index
Snell's Law states:
μ1sini=μ2sinr
Where:
- μ1 is the refractive index of the rarer medium (air, μ1=1).
- μ2 is the refractive index of the denser medium (which we need to find).
- i=60∘
- r=30∘
Substituting the known values into Snell's Law:
1⋅sin(60∘)=μ2⋅sin(30∘)
Step 5: Substitute the sine values
We know:
- sin(60∘)=√32
- sin(30∘)=12
So we have:
√32=μ2⋅12
Step 6: Solve for μ2
Multiplying both sides by 2:
√3=μ2
Thus, the refractive index of the denser medium is:
μ2=√3
Step 7: Calculate the angle of deviation
The angle of deviation D is given by:
D=i−r
Substituting the values:
D=60∘−30∘=30∘
Final Answers
- The refractive index of the denser medium is √3.
- The angle of deviation is 30∘.
---
- A ray of light strikes a denser medium from a rarer medium at an angle of incidence i=60∘.
- The reflected and refracted rays are perpendicular to each other.
Since the reflected and refracted rays are perpendicular, we can denote the angle of refraction as r. The relationship can be expressed as:
i+r=90∘
This means:
r=90∘−i
Substituting the value of i:
r=90∘−60∘=30∘
Snell's Law states:
μ1sini=μ2sinr
Where:
- μ1 is the refractive index of the rarer medium (air, μ1=1).
- μ2 is the refractive index of the denser medium (which we need to find).
- i=60∘
- r=30∘
1⋅sin(60∘)=μ2⋅sin(30∘)
We know:
- sin(60∘)=√32
- sin(30∘)=12
√32=μ2⋅12
Multiplying both sides by 2:
√3=μ2
μ2=√3
The angle of deviation D is given by:
D=i−r
Substituting the values:
D=60∘−30∘=30∘
- The refractive index of the denser medium is √3.
- The angle of deviation is 30∘.
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRAUMENTS Book:NARAYNAChapter:RAY OPTICS AND OPTICAL INSTRAUMENTS Exercise:EXERCISE-2 (H.W)(REFRACTION THROUGH SPHERICAL SURFACES)
Explore 5 Videos
- RAY OPTICS AND OPTICAL INSTRAUMENTS Book:NARAYNAChapter:RAY OPTICS AND OPTICAL INSTRAUMENTS Exercise:EXERCISE-2 (H.W)(LENSES & THEIR COMBINATIONS)
Explore 23 Videos
- RAY OPTICS AND OPTICAL INSTRAUMENTS Book:NARAYNAChapter:RAY OPTICS AND OPTICAL INSTRAUMENTS Exercise:EXERCISE-2 (H.W)(REFLECTION)
Explore 15 Videos
- NUCLEI Book:NARAYNAChapter:NUCLEI Exercise:ASSERTION & REASON
Explore 5 Videos
- SEMI CONDUCTOR DEVICESBook:NARAYNAChapter:SEMI CONDUCTOR DEVICESExercise:Level-II (H.W)
Explore 36 Videos
Similar Questions
A ray of light is going from rarer to denser medium so that when angle of incidence is 60∘ reflected and refracted rays are perpendicular to each other.The refractive index of denser medium w.r.t.rarer medium is
View SolutionA ray of light strikes a glass plate at an angle of incidence 57∘ . If the reflected and refracted rays are perpendicular to each other, what is the refractive index of glass.
View Solution
Knowledge Check
A ray of light strikes a material's slab at an angle of incidence 60∘. If the reflected and refracted rays are perpendicular to each other, the refractive index of the material is
A1√3B1√2C√2D√3A ray of light from a denser medium strikes a rarer medium at an angle of incidence i. if the reflected and the refracted rays are mutually perpendicular to each other, what is the value of the critical angle ?
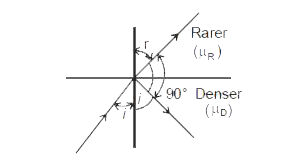 Asin−1(coti)Bcos−1(tani)Csin−1(tani)Dtan−1(sini)
Asin−1(coti)Bcos−1(tani)Csin−1(tani)Dtan−1(sini)A ray of light strikes a glass plate at an angle of 40∘. If the reflected and refracted rays are perpendicular to each other the index of refractive of glass is
A1/2B√3/2C3/2D0.83
A ray of light from a denser medium strikes a rarer medium at an angle of incidence i. if the reflected and the refracted rays are mutually perpendicular to each other, what is the value of the critical angle ?
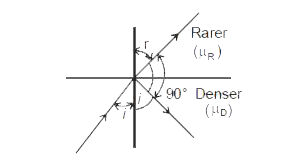
View SolutionA ray of light from a denser medium strikes a rarer medium at an angle of incidence i=tan−1(1/2). If the reflected and the refracted rays are mutually perpendicular to each-other, what is the value of the critical angle in degree?
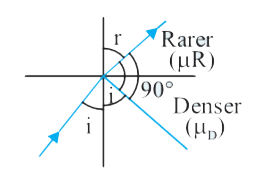
View SolutionA ray of light passes from a denser medium to a rarer medium at an angle of incidence i. The reflected and refracted rays make an angle of 90∘ with each other. The angle of reflection and refraction are resepectively r and r'. The critical angle is given by :
View SolutionA ray of light from a denser medium strikes a rarer medium at angle of incidence i. The refrected and the refracted rays make an angle of 90∘ with each other. The angles of reflection and refraction are r and r′ respectively. The critical angle is
(i) sin−1(tanr)
(ii) sin−1(tani)
(iii) sin−1(tanr)
(iv) tan−1(tani)
View Solution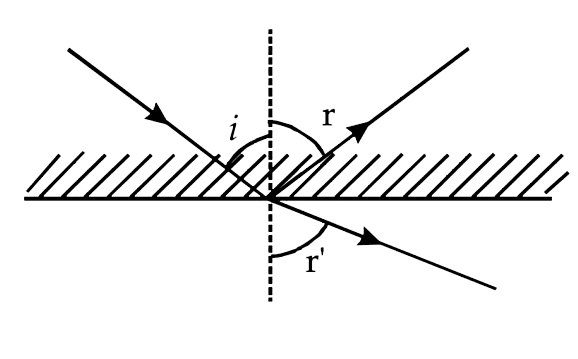
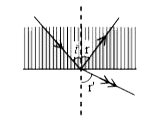
A ray of light from a denser medium strike a rarer medium at an angle of incidence I (see Fig). The reflected and refracted rays make as angle of 90degrees with each other. The angles of reflection and refraction are r and r The critical angle is
View Solution