A ray of light from a denser medium strikes a rarer medium at an angle of incidence i=tan−1(1/2). If the reflected and the refracted rays are mutually perpendicular to each-other, what is the value of the critical angle in degree?
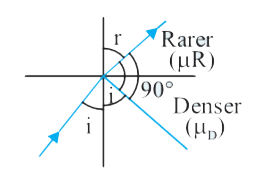
From Snell’s law, we have
sinisinr=μRμD or , μ=μDμR=sinrsini…..(i)
According to the given problem.
i+r+90∘=180∘ or, r=90∘−i
Substituting the above value of r in equation (i), we get
μ=sin(90∘−i)sini or, μ=coti....(ii)
By definition C=sin−1(1μ)or, C=sin−1(1coti)(using equation (ii)
orC=sin−1(tani)=sin−1(1/2)⇒C=π/6=30∘
Similar Questions
A ray of light from a denser medium strikes a rarer medium at an angle of incidence i. if the reflected and the refracted rays are mutually perpendicular to each other, what is the value of the critical angle ?
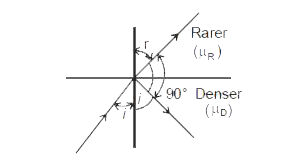
View SolutionA ray of light strikes a glass plate at an angle of incidence 57∘ . If the reflected and refracted rays are perpendicular to each other, what is the refractive index of glass.
View Solution
Knowledge Check
Light from a denser medium 1 passes to a rarer medium 2. When the angle of incidence is θ the partially reflected and refracted rays are mutually perpendicular. The critical angle will be
 Asin−1(cotθ)Bsin−1(tanθ)Csin−1(cosθ)Dsin−1(secθ)
Asin−1(cotθ)Bsin−1(tanθ)Csin−1(cosθ)Dsin−1(secθ)A ray of light from a rarer medium strikes a denser medium at angle of incidence 60°. The reflected and refracted rays are perpendicular to each other. The refractive index of denser medium and angle of deviation respectively are
A√3,30∘B√2,45∘C√3,60∘D√2,30∘A ray of light strikes a material's slab at an angle of incidence 60∘. If the reflected and refracted rays are perpendicular to each other, the refractive index of the material is
A1√3B1√2C√2D√3
When a ray of light travels from a denser medium to a rarer medium, the ray will :
View Solution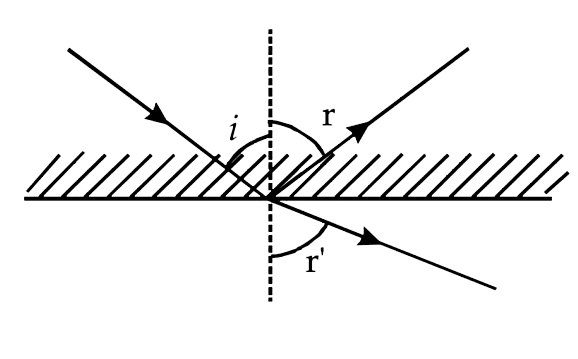
A ray of light from a denser medium strike a rarer medium at an angle of incidence I (see Fig). The reflected and refracted rays make as angle of 90degrees with each other. The angles of reflection and refraction are r and r The critical angle is
View SolutionWhen a ray of light passes from a denser medium to a rarer medium, the ray …………. .
View Solution
A ray of light from a denser medium strike a rarer medium at an angle of incidence I (see Fig). The reflected and refracted rays make as angle of 90degrees with each other. The angles of reflection and refraction are r and r The critical angle is
View SolutionA ray of light from a denser medium strikes a rarer medium at an angle of incidence i. if the reflected and the refracted rays are mutually perpendicular to each other, what is the value of the critical angle ?
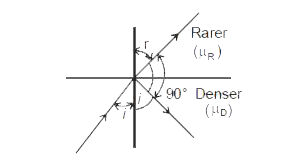
View Solution

