Figure shows variation of acceleration due to gravity with distance from centre of a uniform spherical planet, Radius of planet is R. What is r1−r1
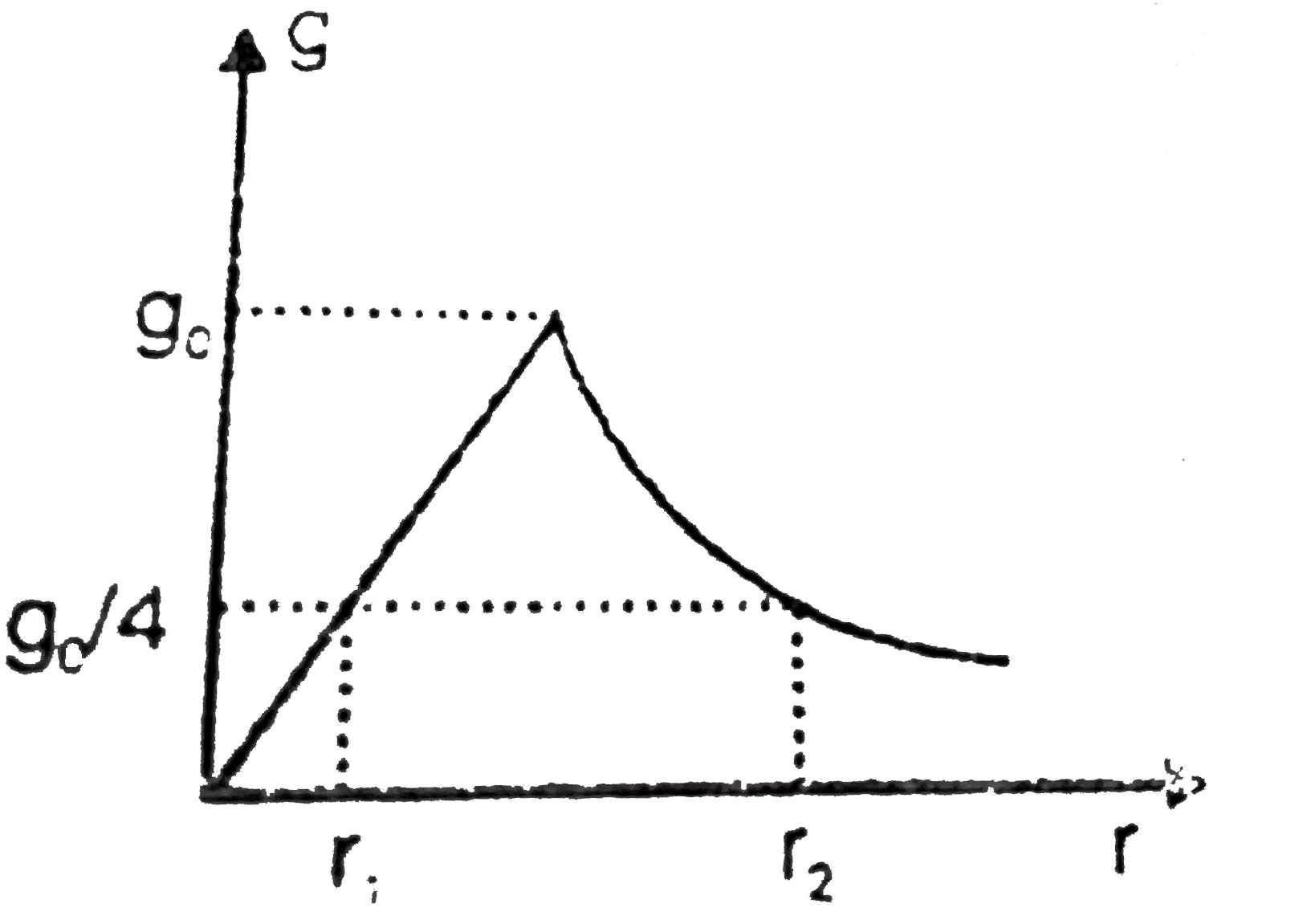
R4
7R4
4R3
2R
The correct Answer is:B
Inside planet
904g0(1−dR)⇒d=3R4
Outside planet
g=g0(R2)(r+h)2⇒h=R .
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.41
Explore 9 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.42
Explore 20 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.39
Explore 9 Videos
- CURRENT ELECTRICITYBook:RESONANCE ENGLISHChapter:CURRENT ELECTRICITYExercise:High Level Problems (HIP)
Explore 19 Videos
- ELECTRO MAGNETIC WAVESBook:RESONANCE ENGLISHChapter:ELECTRO MAGNETIC WAVESExercise:Exercise 3
Explore 27 Videos
Similar Questions
The acceleration due to gravity near the surface of a planet of radius R and density d is proportional to
View SolutionA satellite of mass m is moving in a circular or orbit of radius R around the earth. The radius of the earth is r and the acceleration due to gravity at the surface of the earth is g. Obtain expressions for the following :
(a) The acceleration due to gravity at a distance R from the centre of the earth
(b) The linear speed of the satellite
(c ) The time period of the satellite
View Solution
Knowledge Check
The dependence of acceleration due to gravity g on the distance r from the centre of the earth, assumed to be a sphere of radius R of uniform density is as shown in Fig. below:

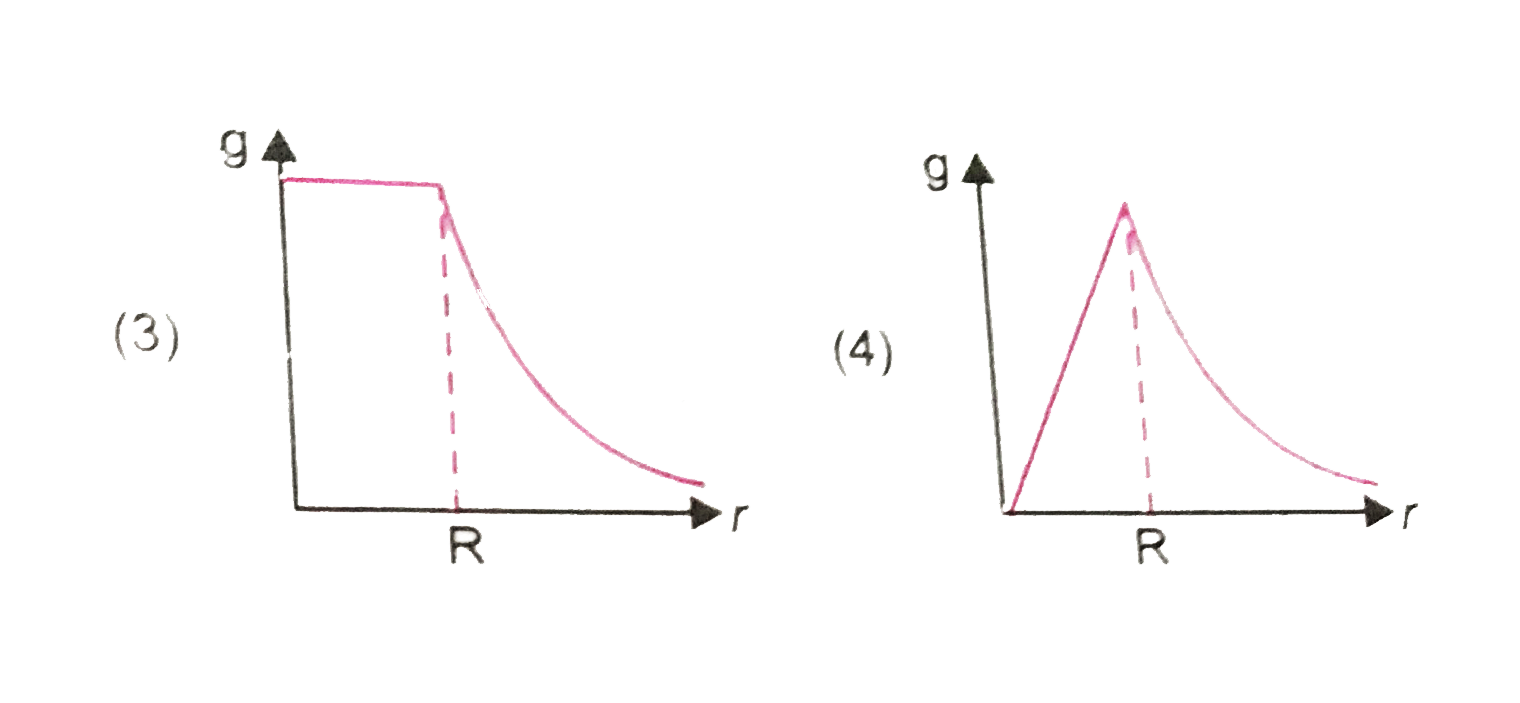
The correct figure isA(i)B(ii)C(iii)D(iv)Which one of the following plots represents the variation of the gravitational field on a particle with distance r due to a thin spherical shell of raduis R? (r is measured from the centre of the spherical shell).
A B
B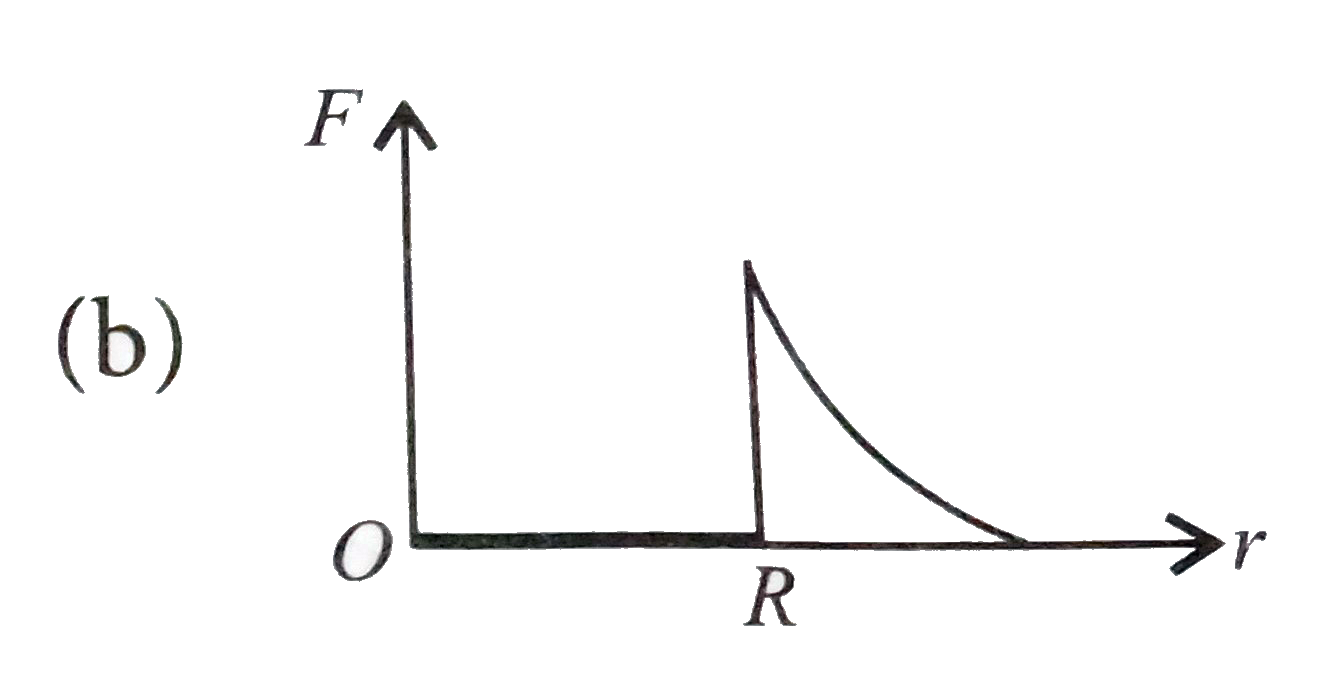 C
C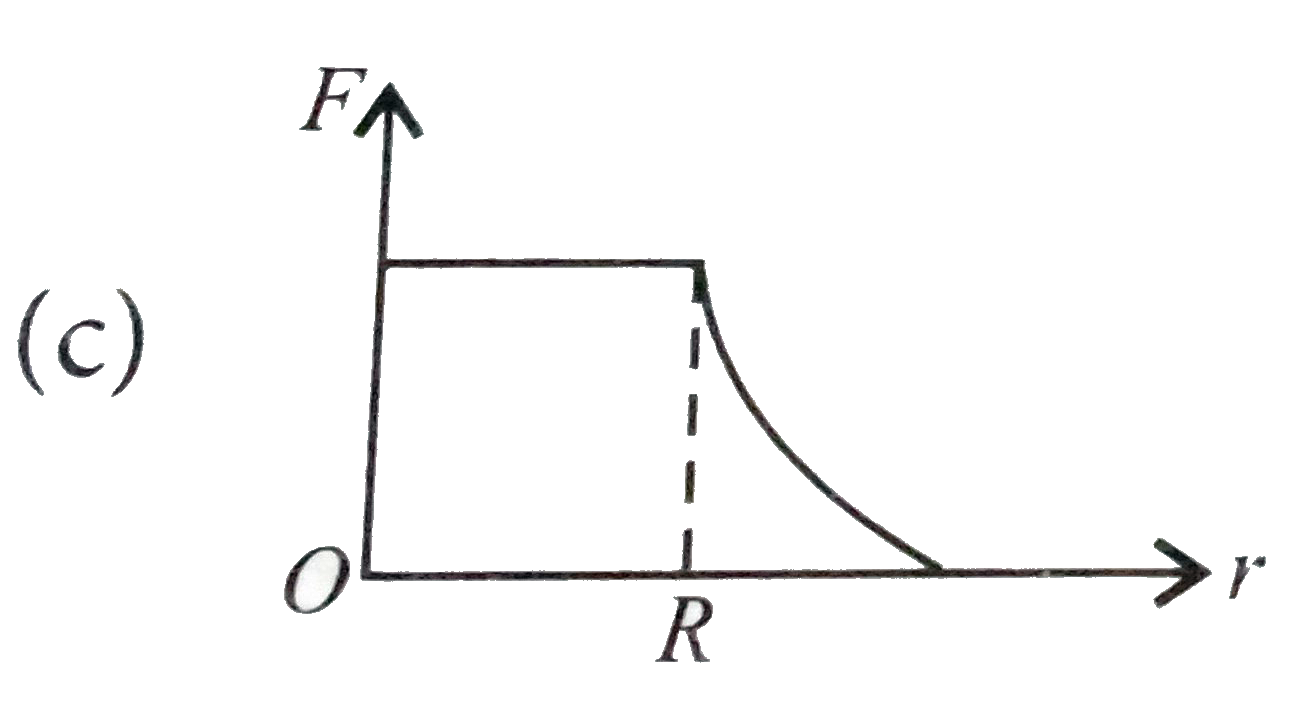 D
D
A : The acceleration due to gravity for an is independent from its mass.
R : The value of 'g ' depends on the mass of planet .
View SolutionIf acceleration due to gravity at distance d [<R] from the centre of earth is β , then its value at distance d above the surface of earth will be [ where R is radius of earth ]
View SolutionThe magnitude of the gravitational field at distance r1 and r2 from the centre of a uniform sphere of radius R and mass M are F1 and F2 respectively. Then:
View SolutionWhich one of the following graphs represents the variation of electric field with distance r from the centre of a charged spherical conductor of radius R?
View SolutionIf earth has uniform density, and radius 'R'. The value of acceleration due to gravity at distance d above the surface is same as the acceleration due to gravity at distance d below the surface. If d=(√x−12)R, then find x.
View SolutionWhat will be the relation the acceleration due to gravity on the surface of the earth and on a planet respectively, whose mass and radius are twice that of the earth ?
View Solution

