The amplitide of a particle due to superposition of following S.H.Ms. Along the same line is
X1=2sin50πtX2=10sin(50πt+37∘)X3=−4sin50πtX4=−12cos50πt
4√2
4
6√2
none of these
The correct Answer is:C
To find the resultant amplitude of the superposition of the given simple harmonic motions (S.H.Ms), we will follow these steps:
Step 1: Identify the Amplitudes and Phases
We have four S.H.Ms given as:
1. X1=2sin(50πt)
2. X2=10sin(50πt+37∘)
3. X3=−4sin(50πt)
4. X4=−12cos(50πt)
From these equations, we can identify the amplitudes and the phases:
- For X1: Amplitude = 2, Phase = 0
- For X2: Amplitude = 10, Phase = 37°
- For X3: Amplitude = 4, Phase = 180° (since −4sin(50πt)=4sin(50πt+180∘))
- For X4: Amplitude = 12, Phase = 90° (since −12cos(50πt)=12sin(50πt+90∘))
Step 2: Resolve Each Component into X and Y Directions
We will resolve the amplitudes into their x and y components using trigonometric identities.
1. For X1:
- Ax1=2
- Ay1=0
2. For X2:
- Ax2=10cos(37∘)
- Ay2=10sin(37∘)
3. For X3:
- Ax3=−4
- Ay3=0
4. For X4:
- Ax4=0
- Ay4=−12
Step 3: Calculate the Total Amplitudes in X and Y Directions
Now, we can sum the components in the x and y directions.
Total Amplitude in X Direction:
Ax=Ax1+Ax2+Ax3+Ax4=2+10cos(37∘)−4+0
Using cos(37∘)≈45:
Ax=2+10⋅45−4=2+8−4=6
Total Amplitude in Y Direction:
Ay=Ay1+Ay2+Ay3+Ay4=0+10sin(37∘)+0−12
Using sin(37∘)≈35:
Ay=0+10⋅35−12=0+6−12=−6
Step 4: Calculate the Resultant Amplitude
The resultant amplitude A can be calculated using the Pythagorean theorem:
A=√A2x+A2y=√62+(−6)2=√36+36=√72=6√2
Final Result
The resultant amplitude of the particle due to the superposition of the given S.H.Ms is 6√2.
---
We have four S.H.Ms given as:
1. X1=2sin(50πt)
2. X2=10sin(50πt+37∘)
3. X3=−4sin(50πt)
4. X4=−12cos(50πt)
- For X1: Amplitude = 2, Phase = 0
- For X2: Amplitude = 10, Phase = 37°
- For X3: Amplitude = 4, Phase = 180° (since −4sin(50πt)=4sin(50πt+180∘))
- For X4: Amplitude = 12, Phase = 90° (since −12cos(50πt)=12sin(50πt+90∘))
We will resolve the amplitudes into their x and y components using trigonometric identities.
- Ax1=2
- Ay1=0
- Ax2=10cos(37∘)
- Ay2=10sin(37∘)
- Ax3=−4
- Ay3=0
- Ax4=0
- Ay4=−12
Now, we can sum the components in the x and y directions.
Ax=Ax1+Ax2+Ax3+Ax4=2+10cos(37∘)−4+0
Using cos(37∘)≈45:
Ax=2+10⋅45−4=2+8−4=6
Ay=Ay1+Ay2+Ay3+Ay4=0+10sin(37∘)+0−12
Using sin(37∘)≈35:
Ay=0+10⋅35−12=0+6−12=−6
The resultant amplitude A can be calculated using the Pythagorean theorem:
A=√A2x+A2y=√62+(−6)2=√36+36=√72=6√2
The resultant amplitude of the particle due to the superposition of the given S.H.Ms is 6√2.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.41
Explore 9 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.42
Explore 20 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.39
Explore 9 Videos
- CURRENT ELECTRICITYBook:RESONANCE ENGLISHChapter:CURRENT ELECTRICITYExercise:High Level Problems (HIP)
Explore 19 Videos
- ELECTRO MAGNETIC WAVESBook:RESONANCE ENGLISHChapter:ELECTRO MAGNETIC WAVESExercise:Exercise 3
Explore 27 Videos
Similar Questions
The resultant amplitude due to superposition of three simple harmonic motions x1=3sinωt,
x2=5sin(ωt+37∘) and x3=−15cosωt is
View SolutionIn case of superposition of waves (at x = 0). y1=4sin(1026πt) and y2=2sin(1014πt)
View SolutionA particle moves along y - axis according to the equation y(in cm)=3sin100πt+8sin250πt−6
View SolutionOn the superposition of two waves [y1=3sin(50πt−20x)] and [y2=3sin(50πt−20x+(π3)]the equation resultant wave will be
View SolutionThe instantaneous potential difference between points.
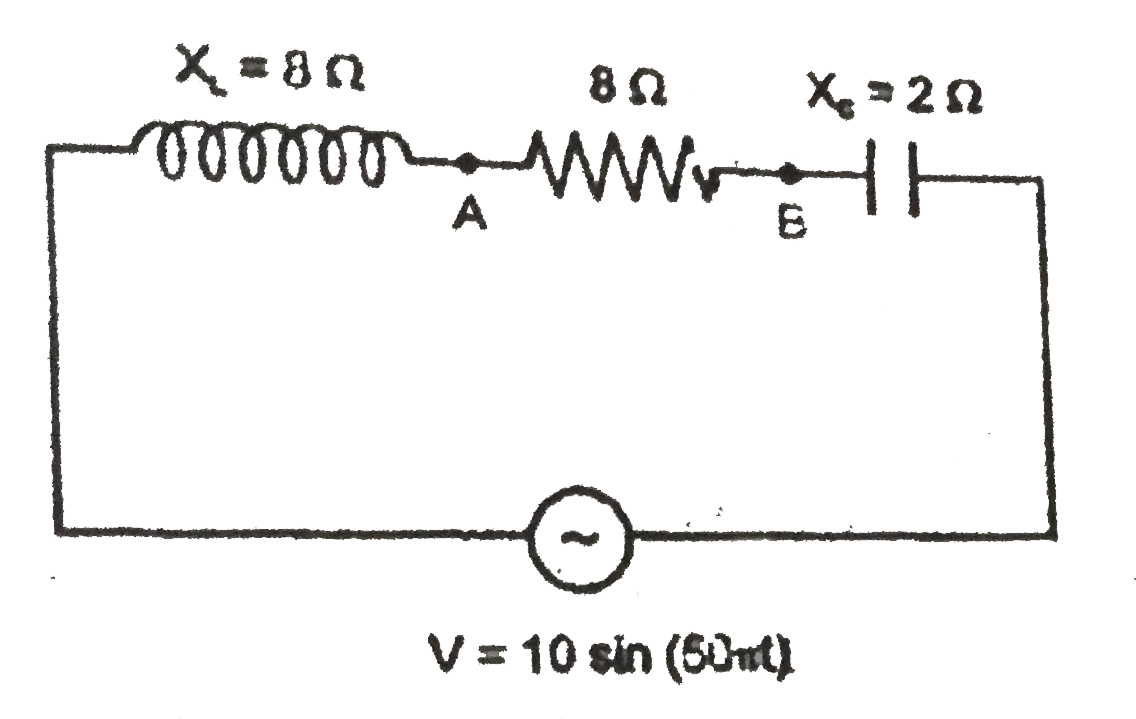
A. 8sin(50πt+37π180)
B. 8sin(50πt−37π180)
C. 10sin(50πt)
D. 10cos(50πt)
View SolutionThe phase difference between two SHMy1=10sin(10πt+π3) and y2=12sin(8πt+π4)to t=0.5s is
View SolutionA 20gm particle is subjected to two simple harmonic motions
x1=2sin10t,
x2=4sin(10t+π3), where x1&x2 are in metre &t is in sec.
View SolutionFind the displacement equation of the simple harmonic motion obtained by combining the motion.
x1=2sinωt, x2=4sin(ωt+π6) and x3=6sin(ωt+π3)
View SolutionDisplacement of a particle executing SHM s x=10(cosπt+sinπt). Its maximum speed is
View SolutionFind the number of beats produced per sec by the vibrations x1=Asin(320πt) and x2=Asin(326πt).
View Solution