The magnitude of the gravitational field at distance r1 and r2 from the centre of a uniform sphere of radius R and mass M are F1 and F2 respectively. Then:
FrF2=r1r2 if r1<R and r2<R
F1F2=r22r21 if r1>R and r2>R
F1F2=r31r32 if r1<R and r2<R
F1F2=r21r22 if r1<R and r2<R
The correct Answer is:A, B
To solve the problem regarding the gravitational field at distances r1 and r2 from the center of a uniform sphere of radius R and mass M, we need to analyze the gravitational field in two scenarios: when the distances are greater than the radius R and when they are less than R.
1. Gravitational Field Outside the Sphere (r1>R and r2>R):
- For a point outside the sphere, the gravitational field F at a distance r from the center is given by:
F=GMr2
- Therefore, the gravitational fields at distances r1 and r2 can be expressed as:
F1=GMr21andF2=GMr22
2. Finding the Ratio F1F2:
- To find the ratio of the gravitational fields F1 and F2:
F1F2=GMr21GMr22=r22r21
3. Gravitational Field Inside the Sphere (r1<R and r2<R):
- For a point inside the sphere, the gravitational field F at a distance r from the center is given by:
F=GMenclosedr2
- The mass enclosed Menclosed can be calculated using the density ρ of the sphere:
Menclosed=ρ⋅V=ρ⋅43πr3
- The density ρ can be expressed as:
ρ=M43πR3
- Thus, substituting this into the expression for Menclosed:
Menclosed=M43πR3⋅43πr3=M⋅r3R3
- The gravitational field inside the sphere becomes:
F=G⋅M⋅r3R3r2=GMR3⋅r
- Therefore, the gravitational fields at distances r1 and r2 inside the sphere are:
F1=GMR3⋅r1andF2=GMR3⋅r2
4. Finding the Ratio F1F2 Inside the Sphere:
- The ratio of the gravitational fields F1 and F2 inside the sphere is:
F1F2=GMR3⋅r1GMR3⋅r2=r1r2
Summary of Results:
- For r1>R and r2>R:
F1F2=r22r21
- For r1<R and r2<R:
F1F2=r1r2
- For a point outside the sphere, the gravitational field F at a distance r from the center is given by:
F=GMr2
- Therefore, the gravitational fields at distances r1 and r2 can be expressed as:
F1=GMr21andF2=GMr22
- To find the ratio of the gravitational fields F1 and F2:
F1F2=GMr21GMr22=r22r21
- For a point inside the sphere, the gravitational field F at a distance r from the center is given by:
F=GMenclosedr2
- The mass enclosed Menclosed can be calculated using the density ρ of the sphere:
Menclosed=ρ⋅V=ρ⋅43πr3
- The density ρ can be expressed as:
ρ=M43πR3
- Thus, substituting this into the expression for Menclosed:
Menclosed=M43πR3⋅43πr3=M⋅r3R3
- The gravitational field inside the sphere becomes:
F=G⋅M⋅r3R3r2=GMR3⋅r
- Therefore, the gravitational fields at distances r1 and r2 inside the sphere are:
F1=GMR3⋅r1andF2=GMR3⋅r2
- The ratio of the gravitational fields F1 and F2 inside the sphere is:
F1F2=GMR3⋅r1GMR3⋅r2=r1r2
- For r1>R and r2>R:
F1F2=r22r21
- For r1<R and r2<R:
F1F2=r1r2
Topper's Solved these Questions
- GRAVITATIONBook:ALLENChapter:GRAVITATIONExercise:Exercise 3 (Miscellaneous Type Questions)
Explore 20 Videos
- GRAVITATIONBook:ALLENChapter:GRAVITATIONExercise:Exercise 4 A (Conceptual Subjective Exercise)
Explore 14 Videos
- GRAVITATIONBook:ALLENChapter:GRAVITATIONExercise:Exercise 1 (Check your Grasp)
Explore 28 Videos
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:subjective
Explore 14 Videos
- KINEMATICS-2DBook:ALLENChapter:KINEMATICS-2DExercise:Exercise (O-2)
Explore 46 Videos
Similar Questions
The magnitude of the gravitational field at distance r1andr_2omthecentreofaunifromsphereofradiusRandmassmareF_1 and F_2 respectively. Then:
View SolutionThe magnitude of gravitational field at distances r1 and r2 from the centre of a uniform sphere of radius R and mass M, respectively. Find the ratio of (I1)/(I2)) if r1>R and r2>R.
View Solution
Knowledge Check
The correct plot of the magnitude of magnetic field →B vs distance r from centre of the wire is, if the radius of wire is R
A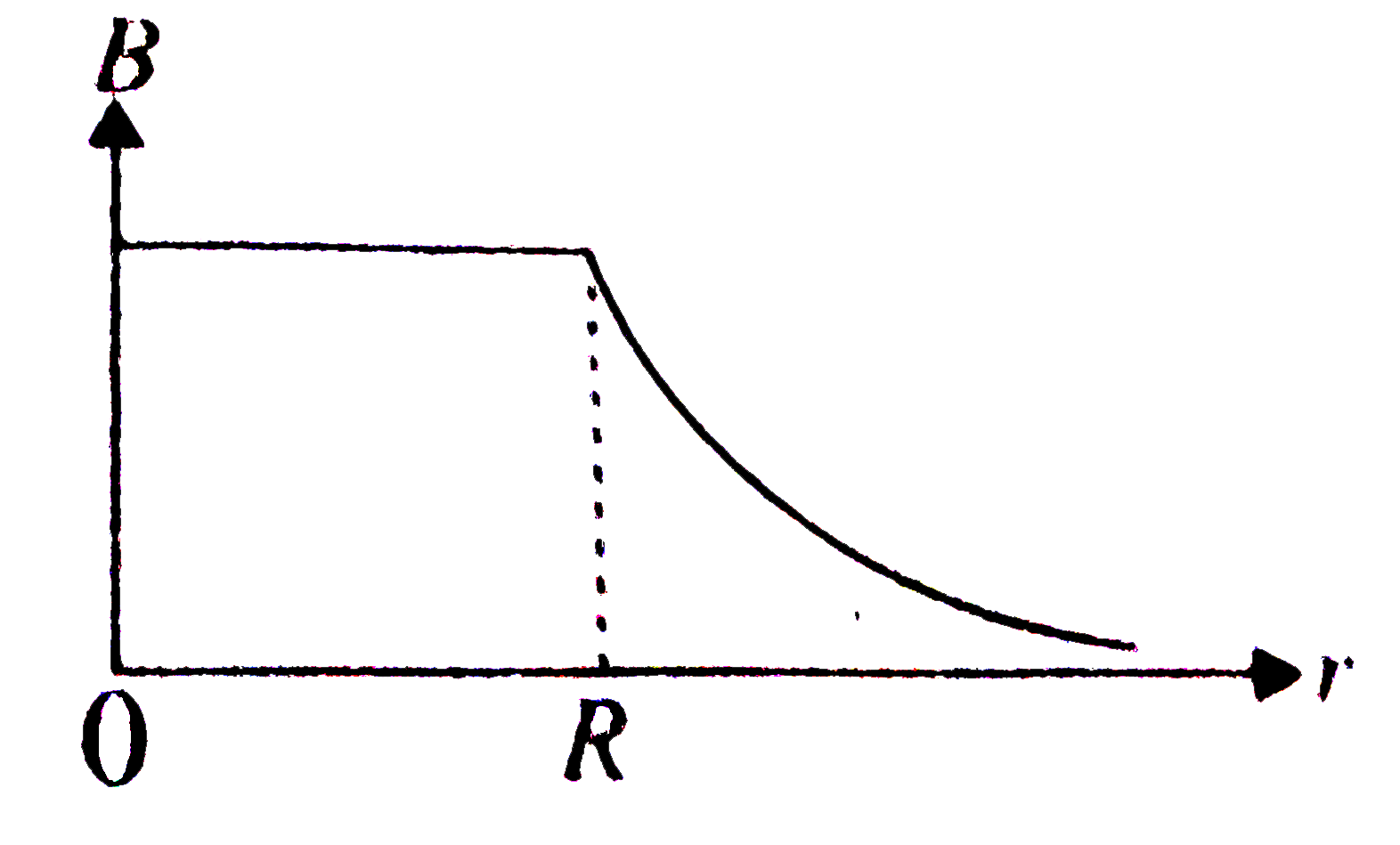 B
B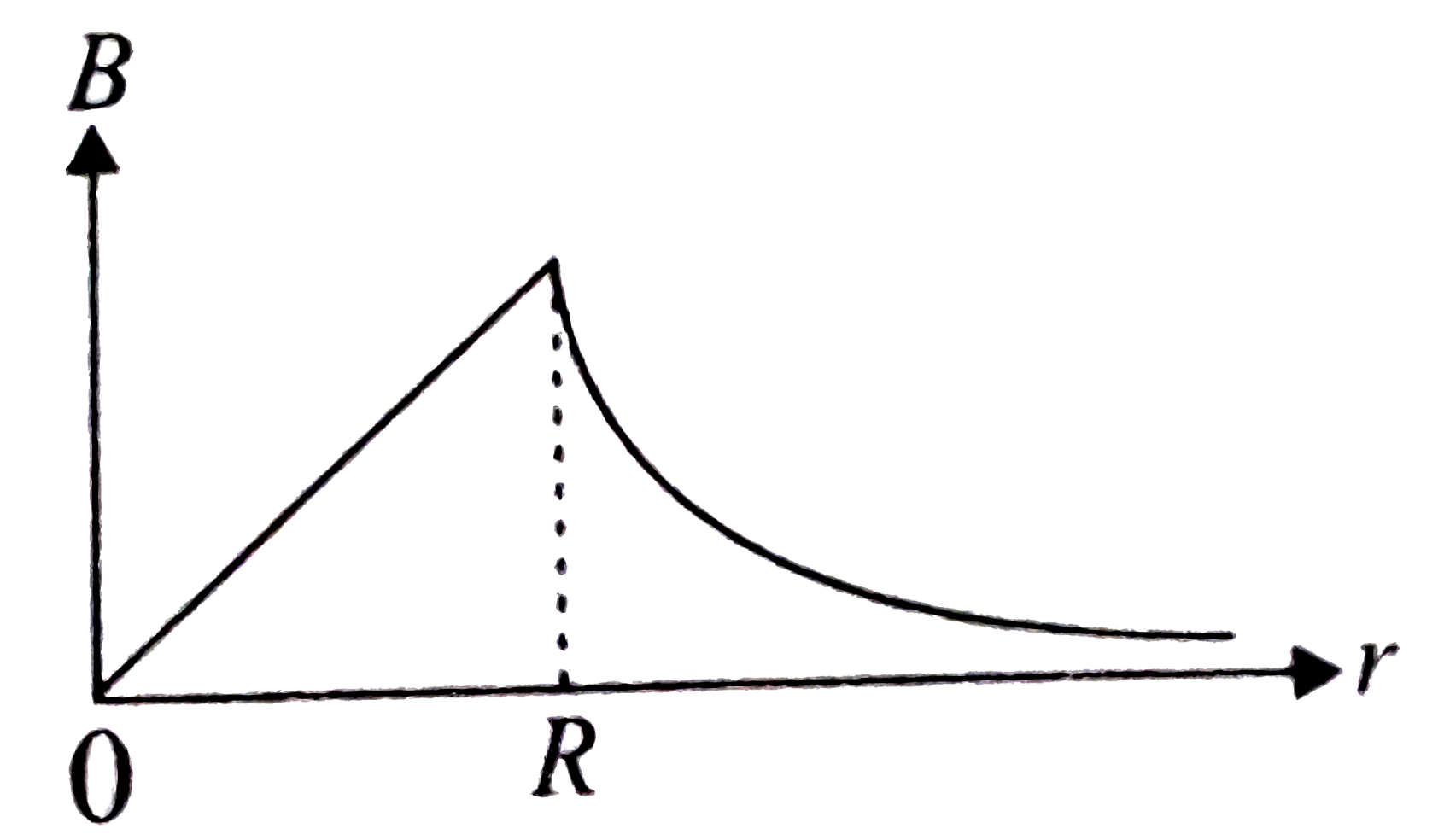 C
C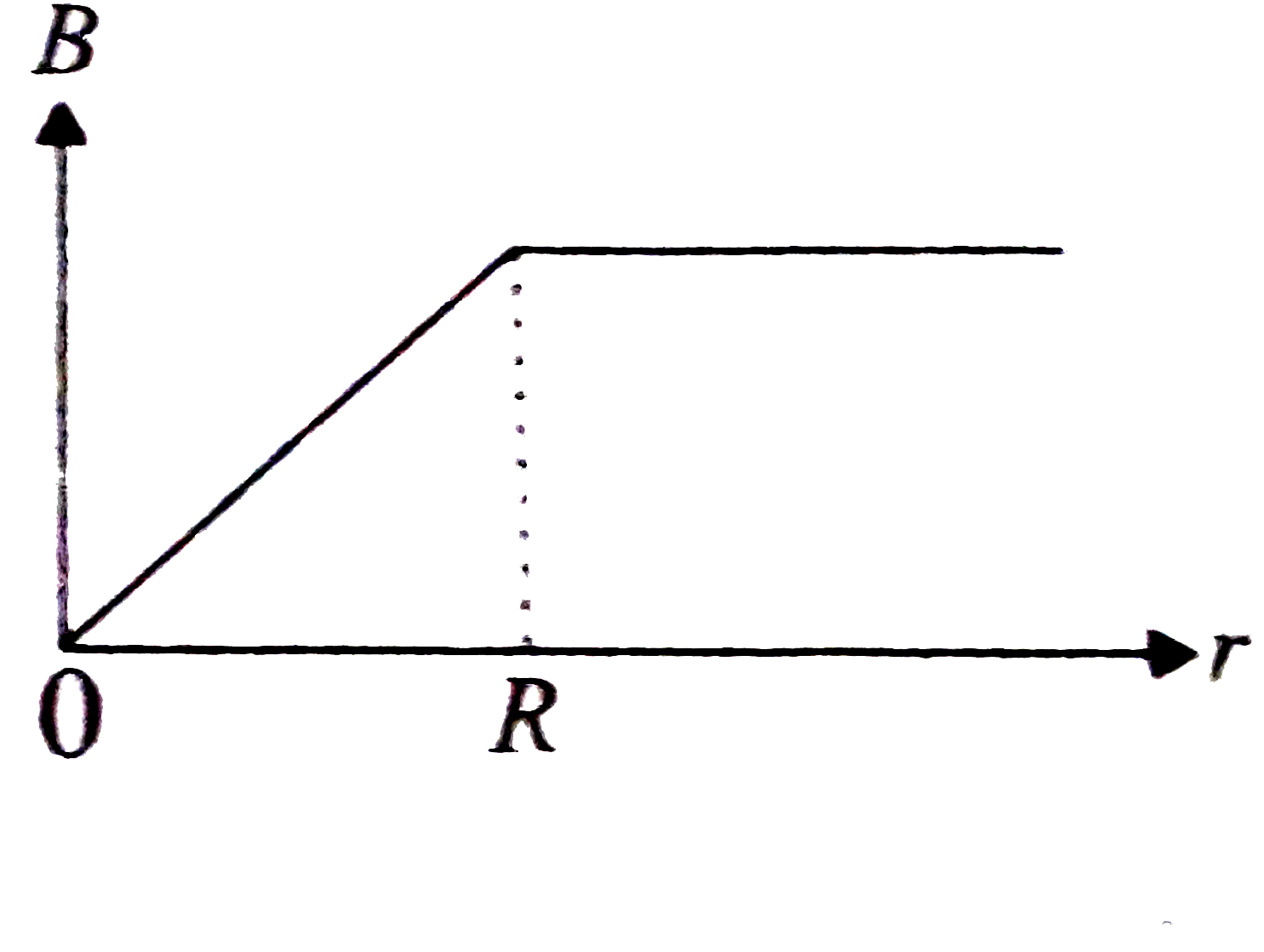 D
D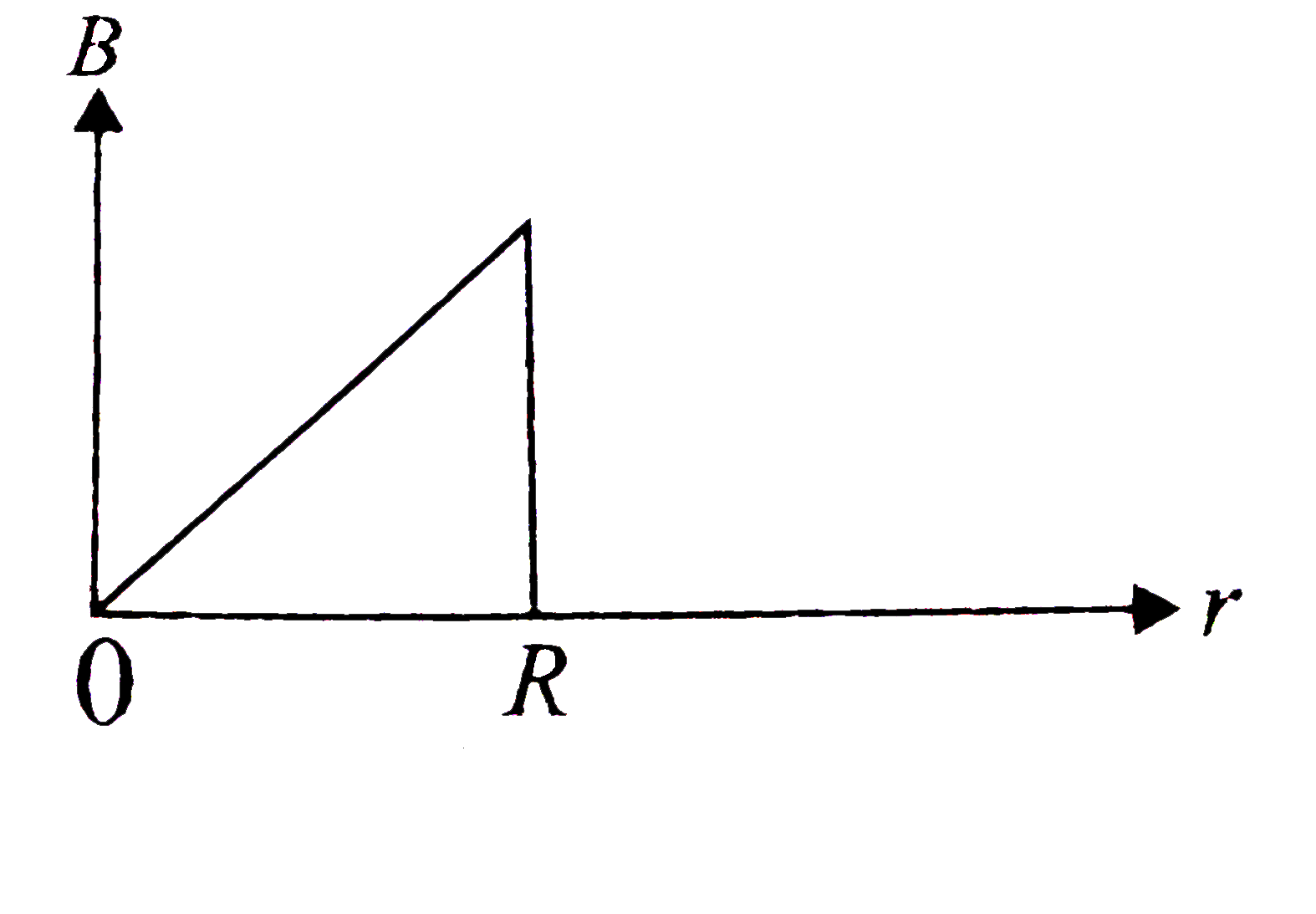
Find potential at a point 'P' at a distance 'x' on the axis away from centre of a uniform ring of mass M and radius R .
View SolutionThe gravitational potential energy of a body at a distance r from the centre of earth is U. Its weight at a distance 2r from the centre of earth is
View SolutionLet V and E represent the gravitational potential and field at a distance r from the centre of a uniform solid sphere. Consider the two statements.
A. the plot of V agasinst r is discotinuous
B. The plot of E against r is discontinuous.
View SolutionFigure shows variation of acceleration due to gravity with distance from centre of a uniform spherical planet, Radius of planet is R. What is r1−r1
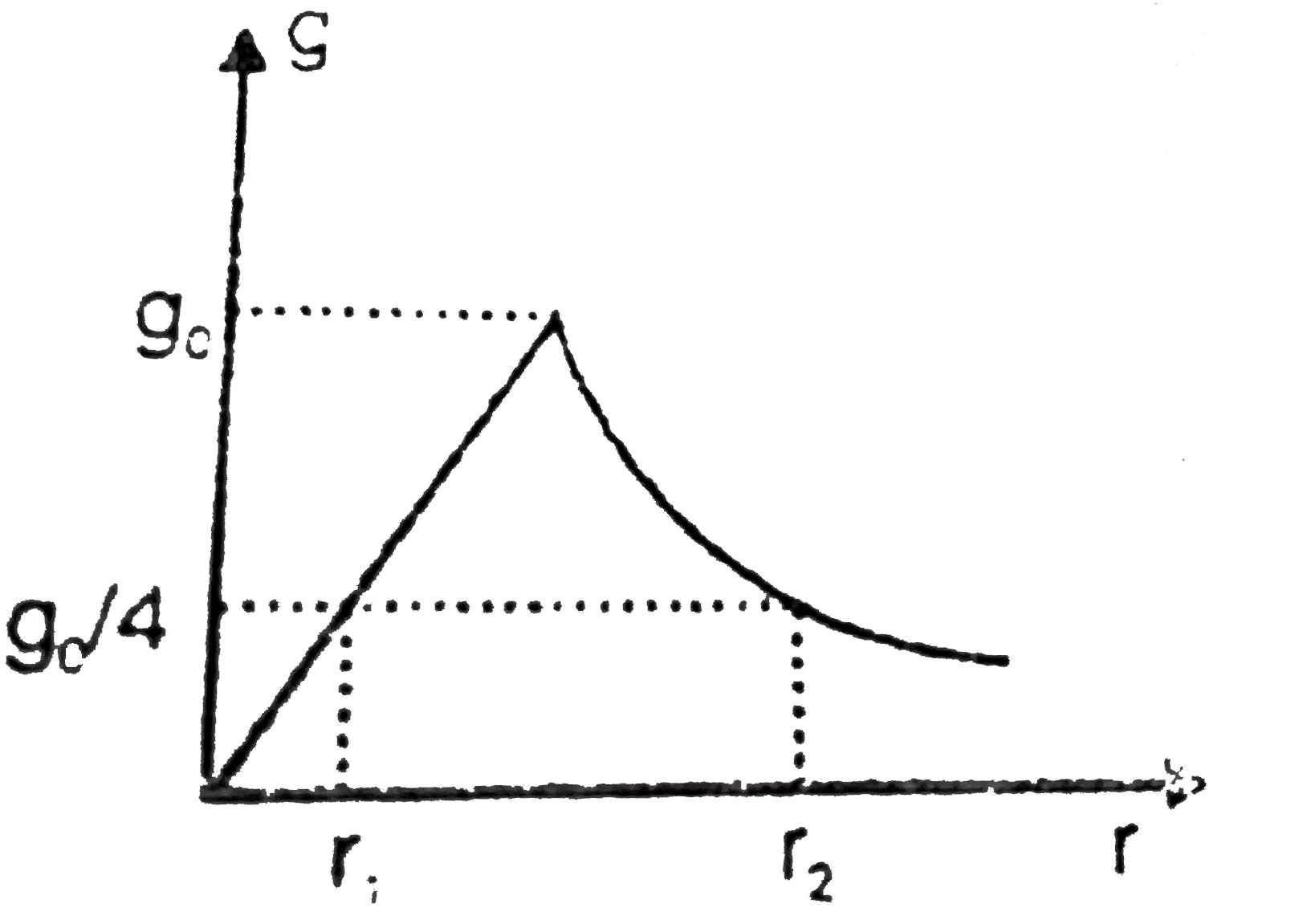
View SolutionThe gravitational field due to an uniform solid sphere of mass M and radius a at the centre of the sphere is
View SolutionFollowing curve shows the variation of intesity of gravitational field (→I) with distance from the centre of solid sphere(r) :
View SolutionA cavity of radius R/2 is made inside a solid sphere of radius R. The centre of the cavity is located at a distance R/2 from the centre of the sphere. The gravitational force on a particle of a mass 'm' at a distance R/2 from the centre of the sphere on the line joining both the centres of sphere and cavity is (opposite to the centre of cavity). [Here g=GM/R2, where M is the mass of the solide sphere]
View Solution