The dependence of acceleration due to gravity g on the distance r from the centre of the earth, assumed to be a sphere of radius R of uniform density is as shown in Fig. below:

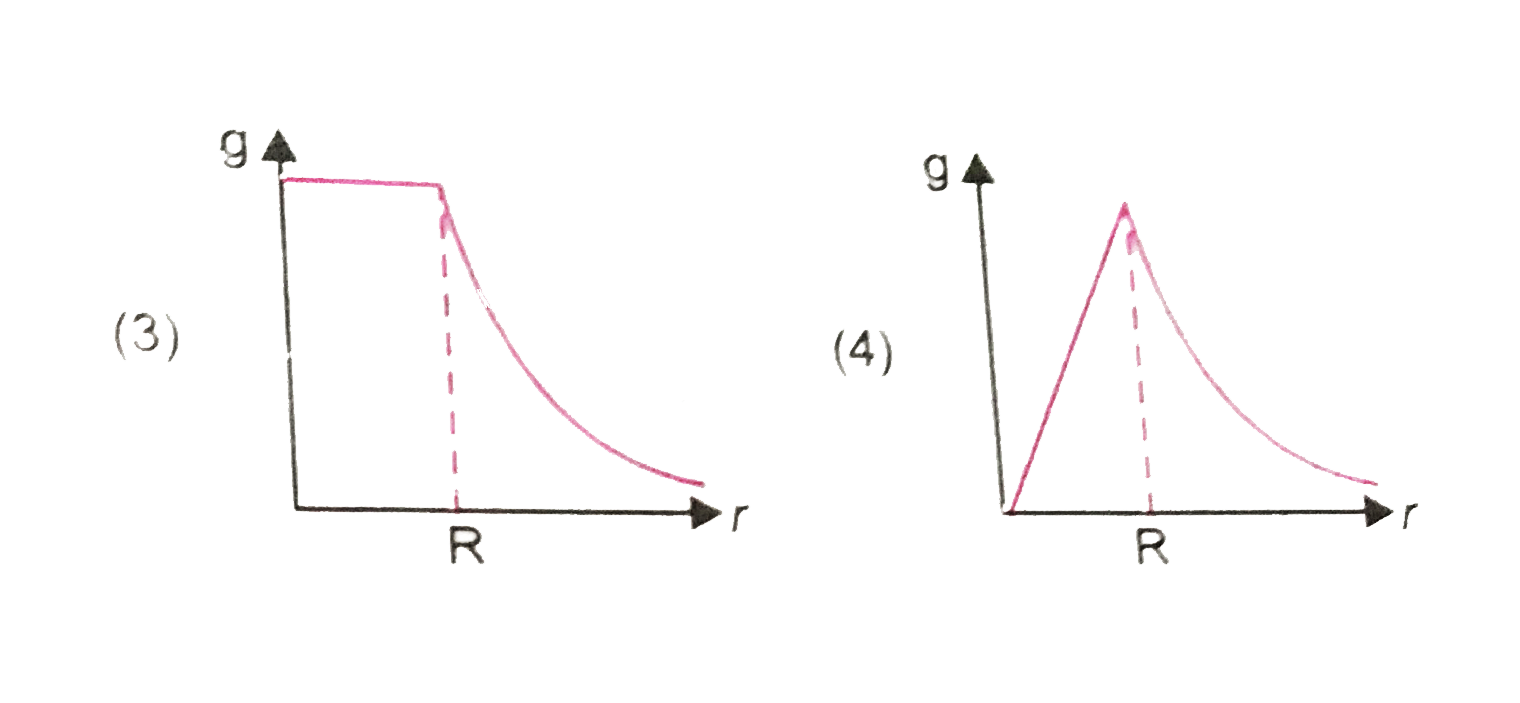
The correct figure is
(i)
(ii)
(iii)
(iv)
The correct Answer is:D
(d) The acceleration due to gravity at a depth d below the surface of earth is
g'=g(1−dR)=g(R−dR)=g(r)R …. (i)
where R-d=r distance of location from the centre of the earth. When r=0, g'=0
From (i), g∝r till R=r, for which g'=g
For r>R,g'=gR2(R+h)2=gR2r2org'∝1r2
Here, R+h=r
Therefore, the variation of g with distance r from centre of earth will be as shown in figure (4). Thus , option (d) is correct.
Topper's Solved these Questions
- GRAVITATIONBOOK - NCERT FINGERTPS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Gravitational Potential energy
7 Videos
- GRAVITATIONBOOK - NCERT FINGERTPS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Escape Speed
7 Videos
- GRAVITATIONBOOK - NCERT FINGERTPS ENGLISHCHAPTER - GRAVITATIONEXERCISE - The Gravitational constant
8 Videos
- KINETIC THEORYBOOK - NCERT FINGERTPS ENGLISHCHAPTER - KINETIC THEORYEXERCISE - Assertion And Reason
10 Videos
Similar Questions
The acceleration due to gravity at a depth R/2 below the surface of the earth is
View SolutionThe value of g (acceleration due to gravity) at earth's surface is 10ms−2. Its value in ms−2 at the centre of the earth which is assumed to be a sphere of radius R metre and uniform mass density is
View SolutionAssuming the earth to be a sphere of uniform density, the acceleration due to gravity
View SolutionThe distance of geostationary satellite from the centre of the earth (radius R) is nearest to
View SolutionFigure shows variation of acceleration due to gravity with distance from centre of a uniform spherical planet, Radius of planet is R. What is r1−r1
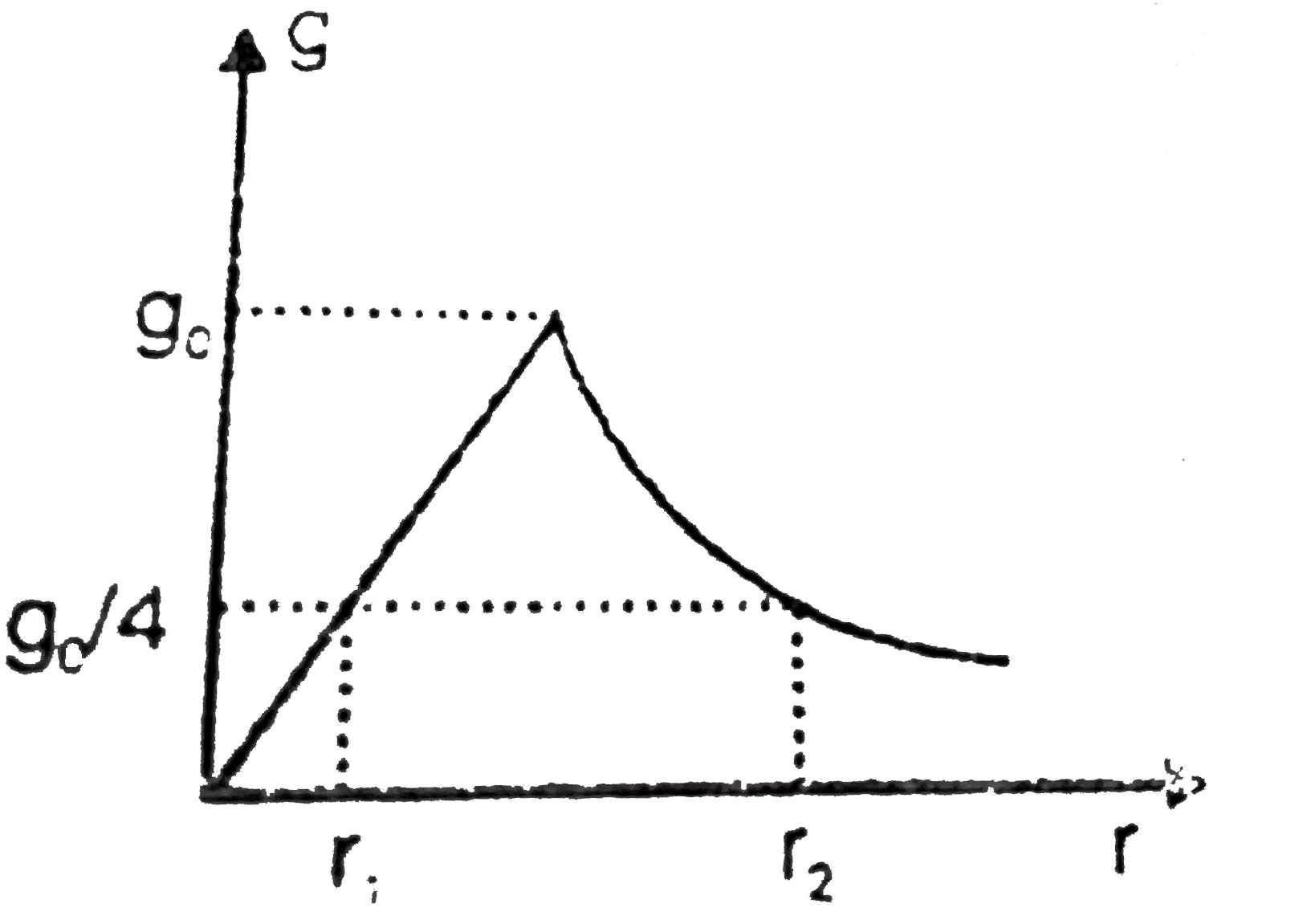
View SolutionWhat will be the acceleration due to gravity at a distance of 3200 km below the surface of the earth ? (Take Re=6400 km)
View SolutionIf acceleration due to gravity at distance d [<R] from the centre of earth is β , then its value at distance d above the surface of earth will be [ where R is radius of earth ]
View SolutionIf g1 and g2 denote acceleration due to gravity on the surface of the earth and on a planet whose mass and radius is thrice that of earth, then
View SolutionStarting from the centre of the earth having radius R, the variation of g (acceleration due to gravity) is shown by
View SolutionIf R is the radius of the earth and g the acceleration due to gravity on the earth's surface, the mean density of the earth is
View Solution
