The value of g (acceleration due to gravity) at earth's surface is 10ms−2. Its value in ms−2 at the centre of the earth which is assumed to be a sphere of radius R metre and uniform mass density is
5
10R
102R
zero
The correct Answer is:D
To find the value of g (acceleration due to gravity) at the center of the Earth, we can use the formula that describes how gravity varies with depth below the Earth's surface.
1. Understanding the Formula:
The formula for the acceleration due to gravity at a depth d below the surface of the Earth is given by:
\(
g' = g \left(1 - \frac{d}{R}\right)
\)
where:
- \( g' \) is the acceleration due to gravity at depth \( d \),
- \( g \) is the acceleration due to gravity at the surface,
- \( R \) is the radius of the Earth.
2. Identifying the Depth at the Center:
At the center of the Earth, the depth \( d \) is equal to the radius \( R \) of the Earth. Therefore, we can substitute \( d = R \) into the formula.
3. Substituting the Values:
Substituting \( d = R \) into the formula gives:
\(
g' = g \left(1 - \frac{R}{R}\right)
\)
4. Simplifying the Expression:
Simplifying the equation:
\(
g' = g \left(1 - 1\right) = g \cdot 0
\)
Thus, we find:
\(
g' = 0
\)
5. Conclusion:
Therefore, the value of acceleration due to gravity \( g' \) at the center of the Earth is:
\(
g' = 0 \, \text{ms}^{-2}
\)
Final Answer:
The value of g at the center of the Earth is \( 0 \, \text{ms}^{-2} \).
---
The formula for the acceleration due to gravity at a depth d below the surface of the Earth is given by:
\(
g' = g \left(1 - \frac{d}{R}\right)
\)
where:
- \( g' \) is the acceleration due to gravity at depth \( d \),
- \( g \) is the acceleration due to gravity at the surface,
- \( R \) is the radius of the Earth.
At the center of the Earth, the depth \( d \) is equal to the radius \( R \) of the Earth. Therefore, we can substitute \( d = R \) into the formula.
Substituting \( d = R \) into the formula gives:
\(
g' = g \left(1 - \frac{R}{R}\right)
\)
Simplifying the equation:
\(
g' = g \left(1 - 1\right) = g \cdot 0
\)
Thus, we find:
\(
g' = 0
\)
Therefore, the value of acceleration due to gravity \( g' \) at the center of the Earth is:
\(
g' = 0 \, \text{ms}^{-2}
\)
The value of g at the center of the Earth is \( 0 \, \text{ms}^{-2} \).
Topper's Solved these Questions
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Multiple Correct
24 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Assertion- Reasoning
13 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Subjective
15 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - INTEGER_TYPE
1 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
Similar Questions
Knowledge Check
The dependence of acceleration due to gravity g on the distance r from the centre of the earth, assumed to be a sphere of radius R of uniform density is as shown in Fig. below:
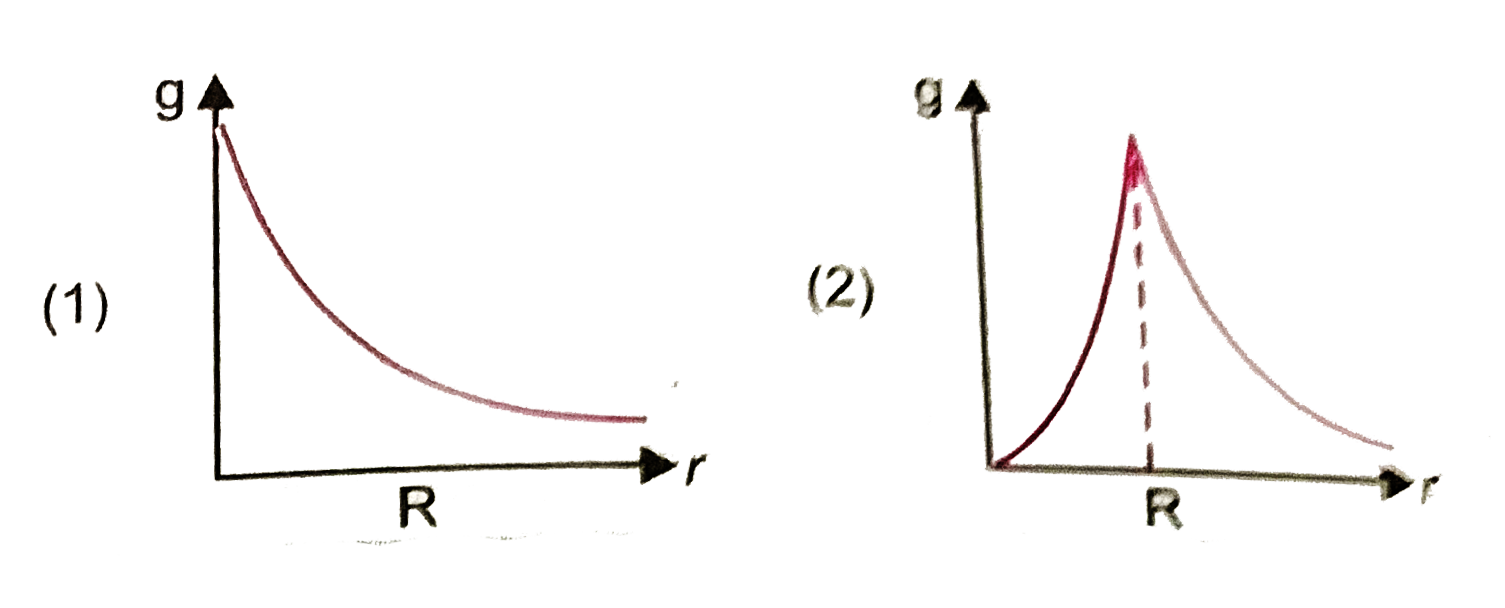
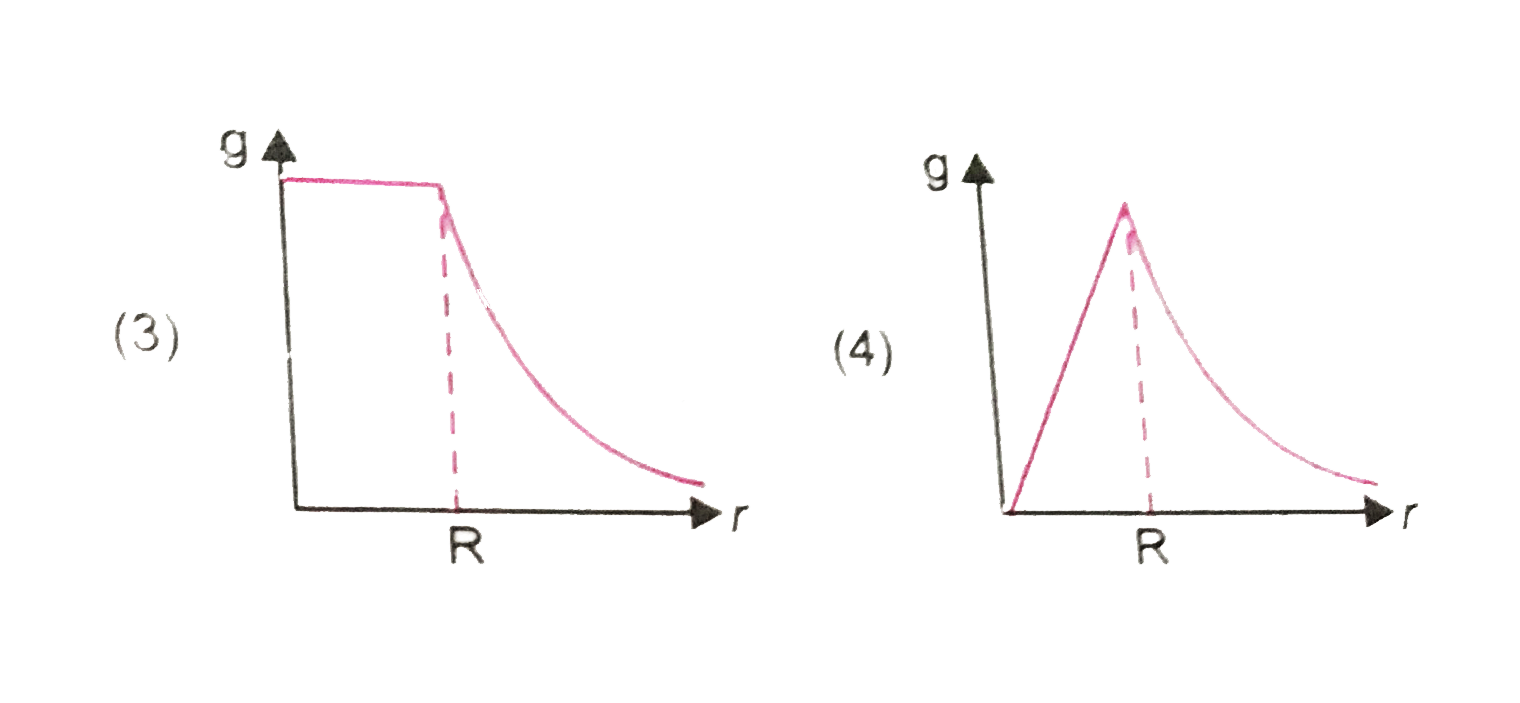
The correct figure isA(i)B(ii)C(iii)D(iv)
If g is the acceleration due to gravity on the surface of the earth , its value at a height equal to double the radius of the earth is
View SolutionThe depth d, at which the value of acceleration due to gravity becomes 1/n times the value at the surface is (R = radius of the earth)
View SolutionIf R is the radius of the earth and g the acceleration due to gravity on the earth's surface, the mean density of the earth is
View SolutionThe value of acceleration due to gravity at Earth's surface is 9.8ms−2.The altitude above its surface at which the acceleration due to gravity decreases to 4.9ms−2m, is close to: (Radius of earth =6.4×106m)
View SolutionThe ratio of acceleration due to gravity at a height 3 R above earth's surface to the acceleration due to gravity on the surface of earth is
(R = radius of earth)
View SolutionHow is the acceleration due to gravity on the surface of the earth related to its mass and radius ?
View SolutionThe density of a newly discovered planet is twice that of earth. The acceleration due to gravity at the surface of the planet is equal to that at the surface of the earth. If the radius of the earth is R, the radius of the planet would be
View Solution
