Two coaxial rings, eacg of radius R, made of thin wire are separated by a small distabce l(l<<R) and carry the charges q and −q. Find the electric field potential and strength at the axis of the system as a function of the x coordinate (see figure). Investigate these functions at |x|>>R
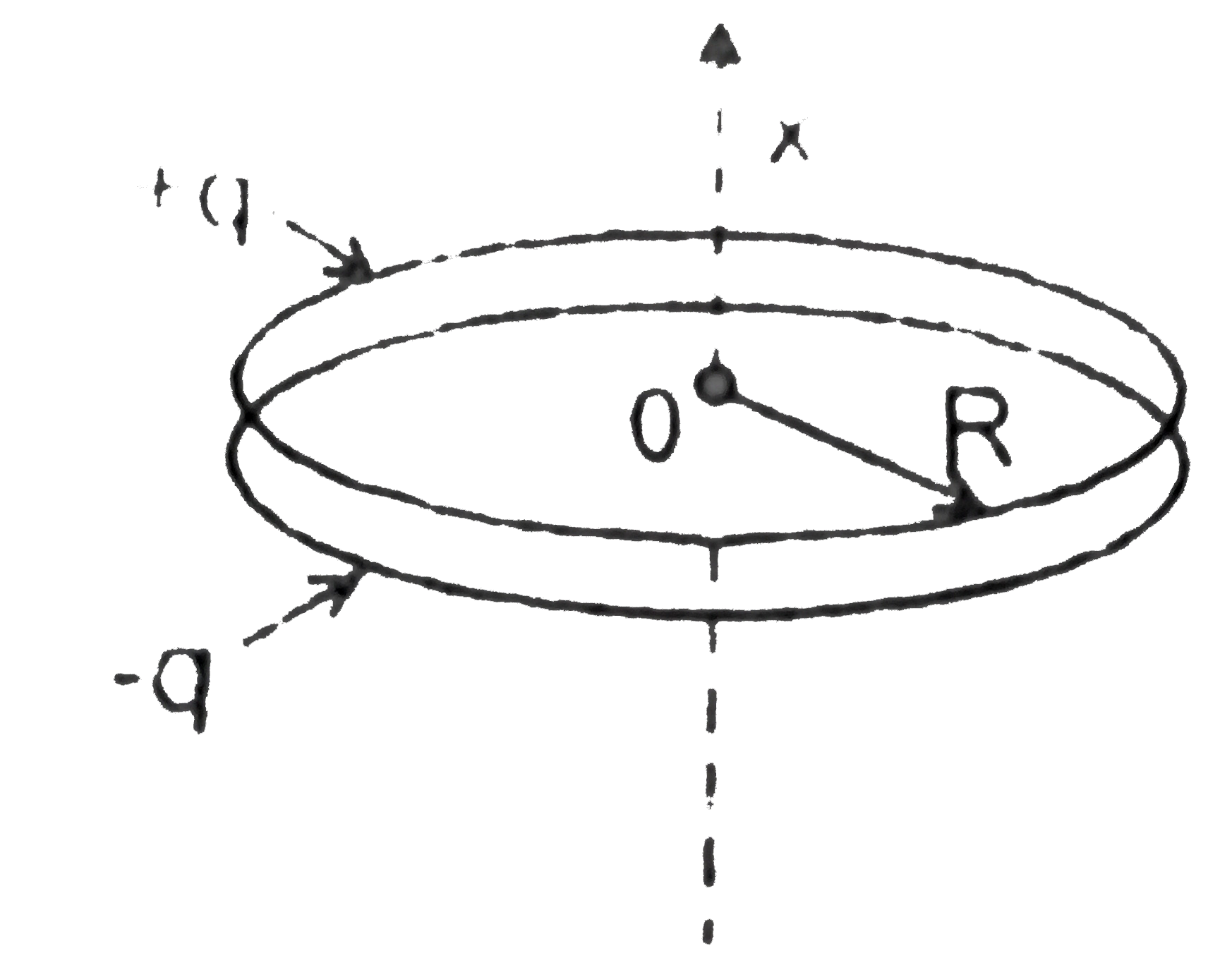
The correct Answer is:V=ql4πε0X(R2+X2)3/2
E=−ql4πε0(R2−2X2)(R2+X2)5/2
V=kq√R2+(x−l2)2−kq√R2+(x+l2)2
∵x>>R Dipole
V=kpr2=kqlx2⇒E=2kpr2=2kqlx3.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.33
Explore 20 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.34
Explore 9 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.31
Explore 20 Videos
- CURRENT ELECTRICITYBook:RESONANCE ENGLISHChapter:CURRENT ELECTRICITYExercise:High Level Problems (HIP)
Explore 19 Videos
- ELECTRO MAGNETIC WAVESBook:RESONANCE ENGLISHChapter:ELECTRO MAGNETIC WAVESExercise:Exercise 3
Explore 27 Videos
Similar Questions
A thin nonconducting ring of radius R has a linear charge density λ=λ0cosφ, where λ0 is a constant , ϕ is the azimuthal angle. Find the magnitude of the electric field strength
(a) at the centre of the ring ,
(b) on the axis of the ring as a function of the distance x from its centre. Investegation the obtained function at x>>R.
View SolutionA point charge q is situated at X between two parallel plates which have a potential difference V and carry charges +Q and −Q. What is the electric field strength at X ?

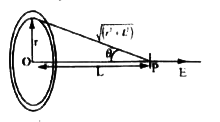
View SolutionA thin wire of radius ..r.. carries a charge q. Find the magnitude of the electric field strength on the axis of the ring as a function of distance L from the centre. Find the same for L>>r Find maximum field strength and the corresponding distance L.
View SolutionThe maximum electric field intensity on the axis of a uniformly charged ring of charge q and radius R will be
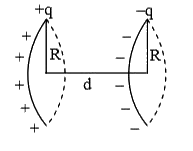
View SolutionTwo thin rings each of radius R are placed at a distance 'd' apart. The charges on the rings are +q and -q. The potential difference between their centres will be -
View SolutionElectric charge Q is uniformly distributed around a thin ring of radius a. find the potential a point P on the axis of the ring at a distance x from the centre of the ring .

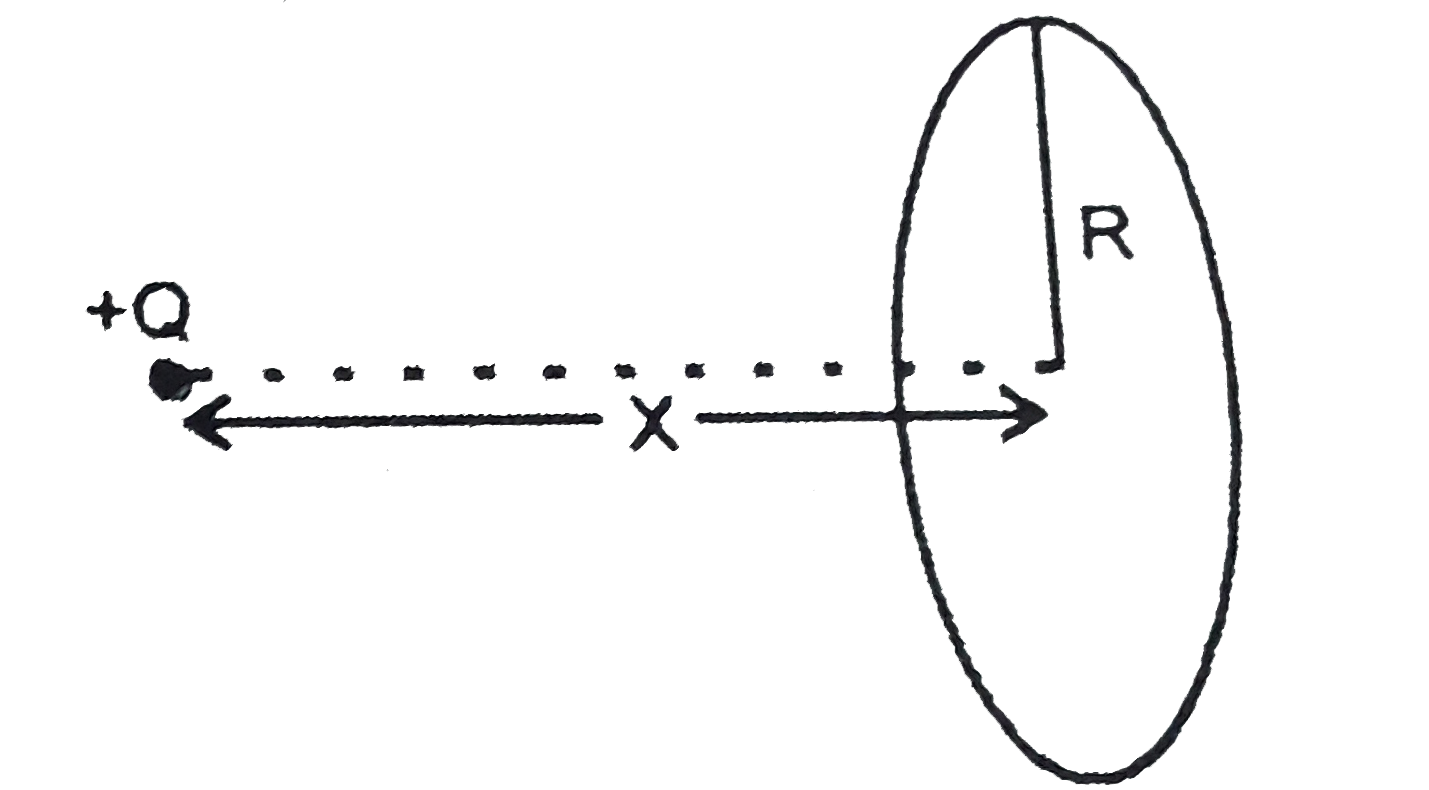
View SolutionFind the electric flux due to a point charge 'Q' through the circular region of radius R if the charge is placed on the axis of ring at a distance x.
View SolutionA circular wire loop of radius R carries a total charge q distributed uniformly over its length. A small length x(<<R) of the wire is cut off. Find the electric field at the centre due to the remaining wire.
View SolutionA ring of radius a contains a charge q distributed. uniformly ober its length. Find the electric field at a point. on the axis of the ring at a distance x from the centre.
View SolutionTwo identical coaxial rings each of radius R are separated by a distance of √3R. They are uniformly charged with charges +Q and −Q respectively. The minimum kinetic energy with which a charged particle (charge +q) should be projected from the centre of the negatively charged ring along the axis of the rings such that it reaches the centre of the positively charged ring is
View Solution