A horizontal cylinder is fixed, its inner surface is smooth and its radius is R. A small block is initially at the lowest point. The minimum velocity that should by given to the block at the lowest point, so that it can just cross the point P is u then
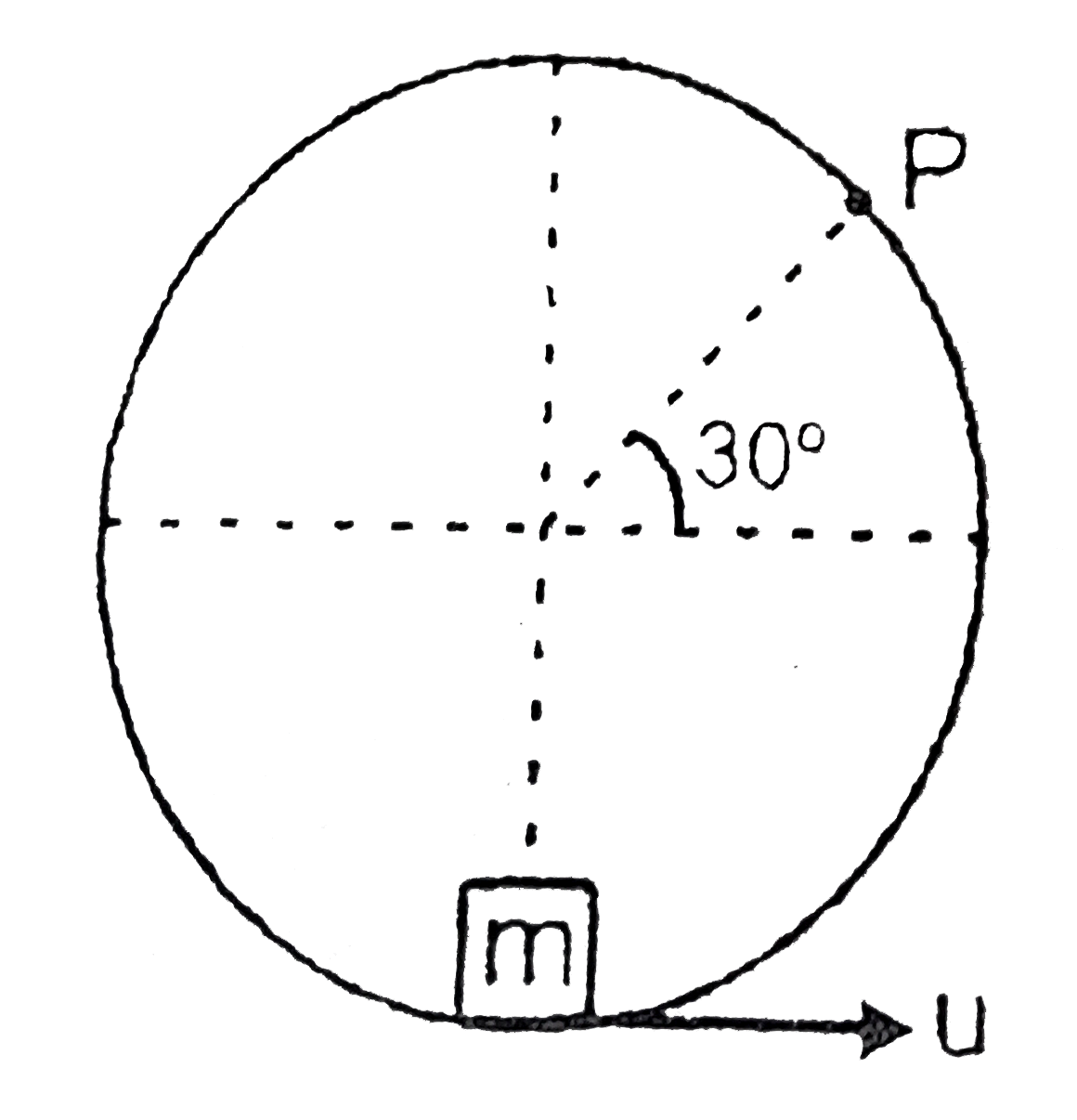
If the block moves anti clockwise then u=√3.5gR
If the block moves anti clockwise then u=√3gR
If the block moves clockwise then u=√3.5gR
If the block moves clockwise then u=√5gR
The correct Answer is:A, D
N=μ2R+mg(3cosθ−2), at θ=120∘N
=0⇒N=mu2R+mg(3cos120∘−2)=0
⇒u=√3.5gR
If the block is moving clockwise, then to cross the point P, the block has to cross the highest point, so to cross the highest point
=√5gR.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.33
Explore 20 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.34
Explore 9 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.31
Explore 20 Videos
- CURRENT ELECTRICITYBook:RESONANCE ENGLISHChapter:CURRENT ELECTRICITYExercise:High Level Problems (HIP)
Explore 19 Videos
- ELECTRO MAGNETIC WAVESBook:RESONANCE ENGLISHChapter:ELECTRO MAGNETIC WAVESExercise:Exercise 3
Explore 27 Videos
Similar Questions
The maximum velocity at the lowest point, so that the string just slack at the highest point in a vertical circle of radius l.
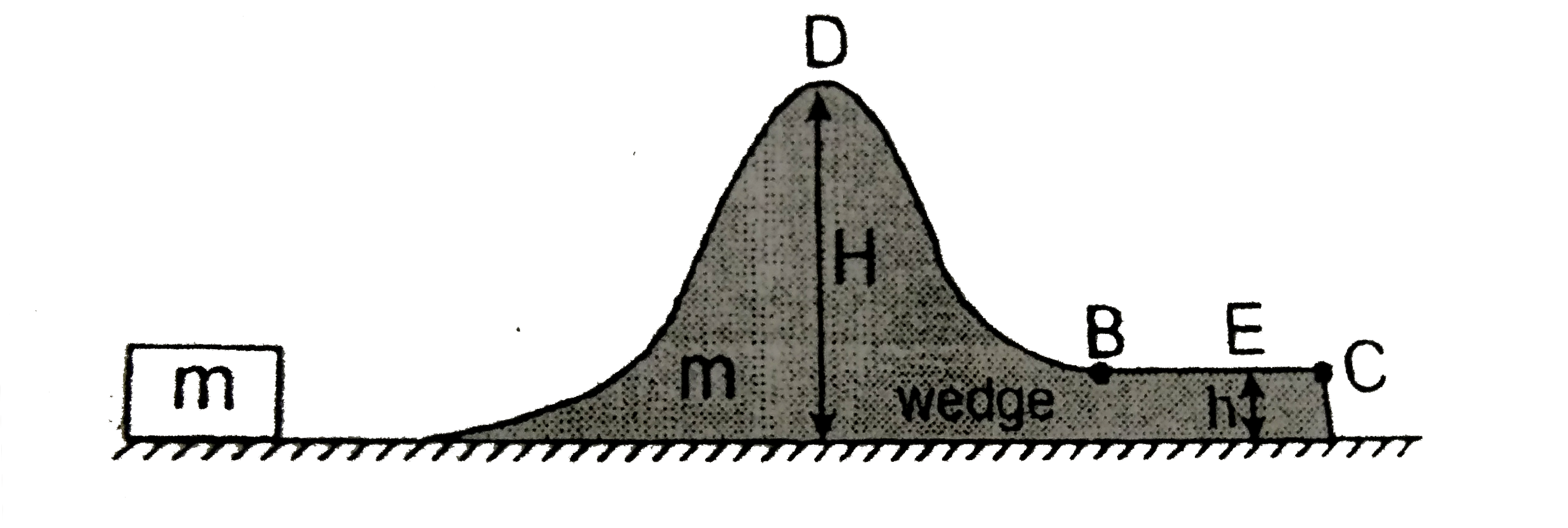
View SolutionFigure shows an irregular wedge of mass m placed on a smooth horizontal surface. Part BC is rough.
What minimum velocity should be imparted to a small block of same mass m so that it may each point B :
View SolutionA bob is attached to a string of length l whose other end is fixed and is given horizontal velocity at the lowest point of the circle so that the bob moves in a vertical plane. Match the velocity given at the lowest point of circle in column I with tension and velocity at the highest point of the circle corresponding to velocity of column I of column II

View SolutionIn the above question, the velocity of the image of Q in plane mirror of block P with respect to ground when Q is at the lowest point first time is:
View Solution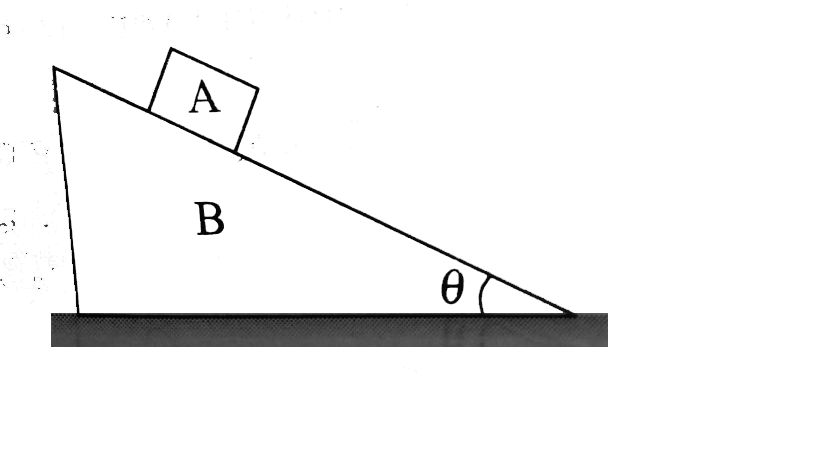
A block is placed on a smooth wedge of inclination angle θ with the horizontal. What minimum acceleration should be given to the wedge in the horizontal direction so that the block starts moving up along the incline?
View SolutionThe diagram show a small bead of mass m carrying charge q. The bead can freely move on the smooth fixed ring placed on a smooth horizontal plane . In the same pane a charge +Q has also been fixed as shown. The potential at the point P due to +Q is V . The velocity which the bead should projected from the point P so that it can complete a circle should be greater than .

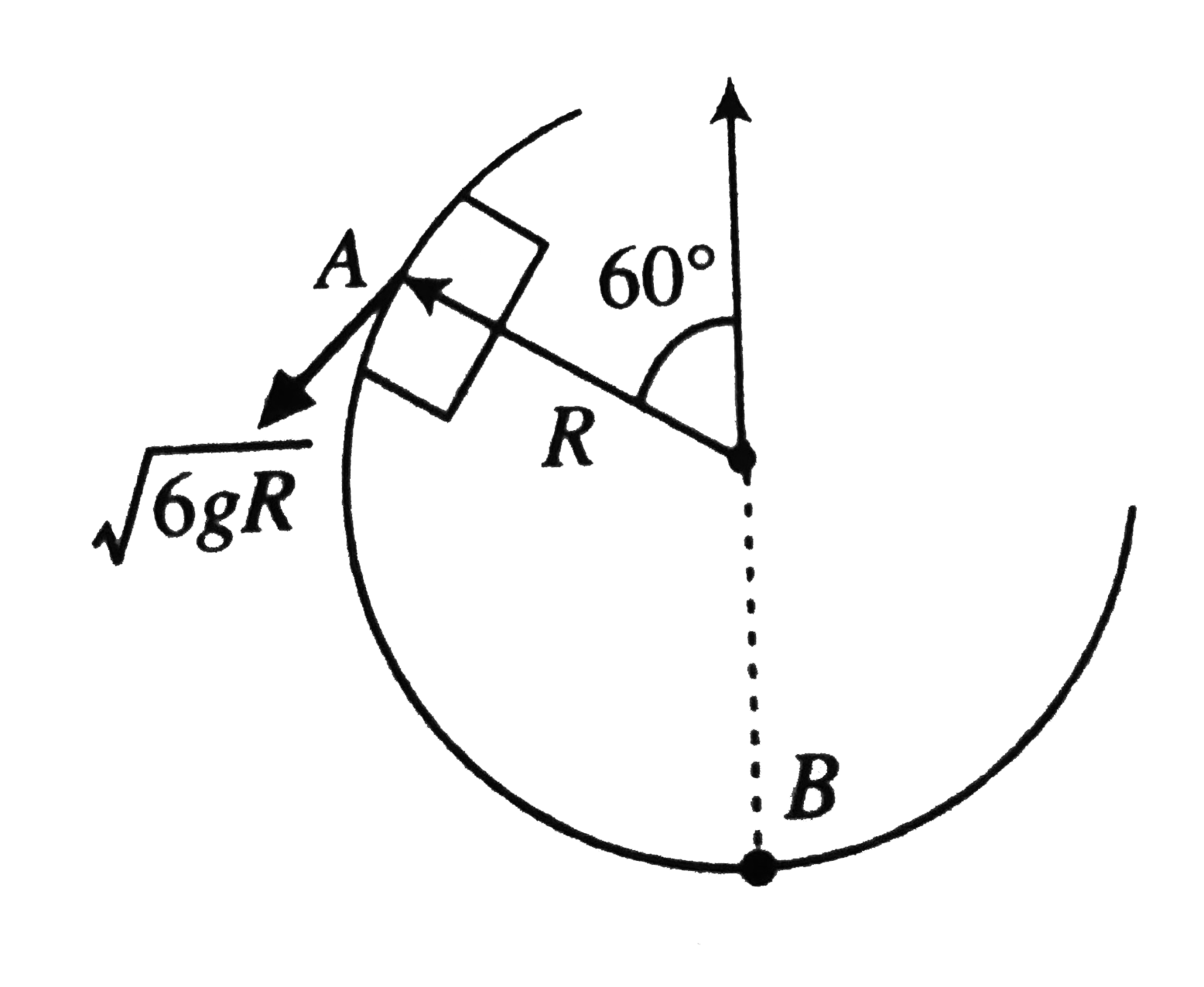
View SolutionFigure shows a smooth vertical circular track AB of radius R. A block slides along the surface AB when it is given a velocity equal to √6gR at point A. The ratio of the force exerted by the track on the block at point A to that at point B is
View SolutionA solid sphere of radius R is placed on a smooth horizontal surface. A horizontal force F is applied at height h from the lowest point. For the maximum acceleration of the centre of mass
View SolutionA solid sphere of radius R is placed on a smooth horizontal surface. A horizontal force F is applied at height h from the lowest point. For the maximum acceleration of the centre of mass
View SolutionAssertion For looping a verticla loop of radius, r the minimum velocity at lowest point should be √5gr. Reason In this event the velocityh at the highest point will be zero.
View Solution