A chain of mass 'm' and radius 'r' is placed onto a cone of semi vertical angle θ. Cone rotated with angular velocity ω. Find the tension in the chain if it does not slide on the cone.
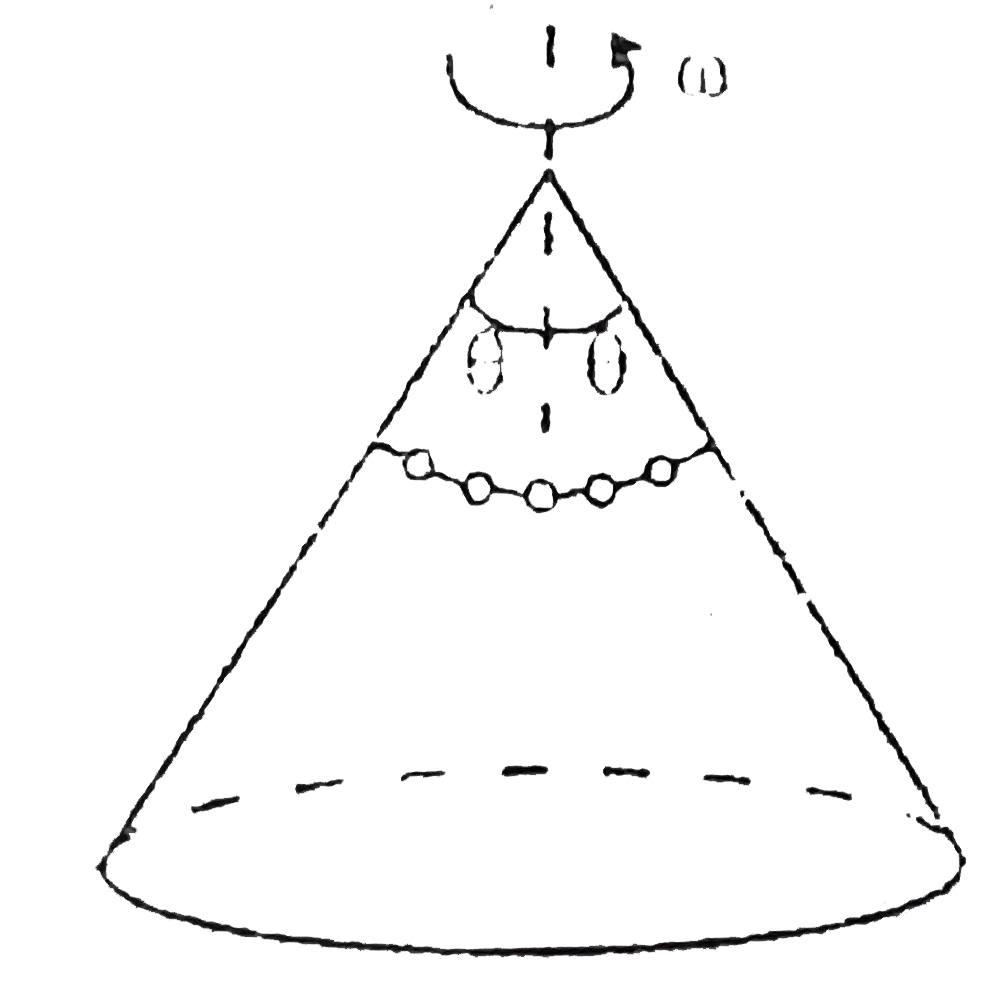
The correct Answer is:M2π(ω2R+gcotθ)

From F.B.D of chain element
Nsinθ=Δmg=λR(2α)g…(i)
2Tsinα−Ncosθ=Δmω2R=λR(2α)ω2R ….(ii)
for small α,sinα=α
From (i) and (ii)
2Tα−λR(2α)gsinθ×cosθ=λR(2α)ω2R
⇒2Tα=λR(2α)ω2R+λR(2α)gcotθ
⇒T=λω2R2+λRcotθ
=λR[ω2R+gcotθ]
=MR2π[ω2R+gcotθ]
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.33
20 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.34
9 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.31
20 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
19 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
A ring of mass m and radius R is given a charge q. It is then rotated about its axis with angular velocity ω.Find
(iii)Magnetic moment of ring.
View SolutionA ring of radius 'r' and mass per unit length 'm' rotates with an angular velocity 'ω' in free space then tension will be :
View SolutionA ring of mass m and radius R is given a charge q. It is then rotated about its axis with angular velocity ω.Find
(ii) Magnetic field produced at the centre of ring.
View SolutionA ring of mass m and radius R is given a charge q. It is then rotated about its axis with angular velocity ω.Find
(i)Current produced due to motion of ring
View SolutionA chain of mass m forming a circle of radius R is slipped on a smooth round cone with half- angle θ. Find the tension in the chain if it rotates with a constant angular velocity ω about a vertical axis coinciding with the symmetry axis of the cone .
View SolutionA thin circular ring of mass M and radius R is rotating in a horizontal plane about an axis vertical to its plane with a constant angular velocity ω. If two objects each of mass m be attached gently to the opposite ends of a diameter of the ring, the ring will then rotate with an angular velocity
View SolutionA thin circular ring of mass M and radius R is rotating in a horizontal plane about an axis vertical to its plane with a constant angular velocity ω. If two objects each of mass m be attached gently to the opposite ends of a diameter of the ring, the ring will then rotate with an angular velocity
View SolutionA ring of mass m and radius R rests in equilibrium on a smooth cone of semi-vertical angle 45∘ as shown. The radius of the cone is 2R. the radius of circular cross section of the ring is r(r<<R).
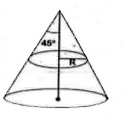
What will be the tension in the ring?
View SolutionA thin circular ring of mass m and radius R is rotating about its axis perpendicular to the plane of the ring with a constant angular velocity ω. Two point particleseach of mass M are attached gently to the opposite end of a diameter of the ring. The ring now rotates, with an angular velocityω2. Then the ratiomM is
View SolutionA ring of mass m and radius R is being rotated about its axis with angular velocity o. If o increases then tension in ring
View Solution
