In the above question, the velocity of the image of Q in plane mirror of block P with respect to ground when Q is at the lowest point first time is:
√2mg2K
√4mg2K
√3mg2K
0
The correct Answer is:D
To solve the problem, we need to analyze the motion of the masses P and Q attached to their respective springs and determine the velocity of the image of Q in the plane mirror of block P when Q is at its lowest point for the first time.
1. Understanding the System:
- We have two masses, P and Q, attached to springs with spring constants 4K and K, respectively.
- Both masses can oscillate independently, executing simple harmonic motion (SHM).
2. Finding the Time Periods:
- The time period (T) for a mass-spring system is given by the formula:
T=2π√mk
- For mass P (attached to spring constant 4K):
TP=2π√M4K=π√MK
- For mass Q (attached to spring constant K):
TQ=2π√MK
- From this, we can see that:
TQ=2TP
- This means the time period of Q is twice that of P.
3. Understanding the Motion:
- When Q is at its lowest point for the first time, it has completed half of its oscillation (downward motion).
- Since T_Q is twice T_P, it implies that while Q is at its lowest point, mass P would have completed its full oscillation (up and down).
4. Velocity at the Lowest Point:
- At the lowest point of its motion, the velocity of mass Q is zero (as it momentarily stops before changing direction).
- The velocity of mass P at this moment can be determined by its motion characteristics. Since P oscillates faster, it would be at its mean position when Q is at its lowest point.
5. Velocity of P:
- The velocity of mass P at its mean position is at its maximum.
- The maximum speed vmax for a mass in SHM is given by:
vmax=ωA
- Where ω=2πT and A is the amplitude of oscillation.
6. Relative Velocity:
- Since Q is at its lowest point (velocity = 0) and P is at its mean position (velocity = maximum), the velocity of the image of Q in the mirror of block P with respect to the ground is equal to the velocity of P.
- Therefore, the velocity of the image of Q is equal to the velocity of P.
Final Answer:
The velocity of the image of Q in the plane mirror of block P with respect to the ground when Q is at the lowest point for the first time is equal to the maximum velocity of mass P.
- We have two masses, P and Q, attached to springs with spring constants 4K and K, respectively.
- Both masses can oscillate independently, executing simple harmonic motion (SHM).
- The time period (T) for a mass-spring system is given by the formula:
T=2π√mk
- For mass P (attached to spring constant 4K):
TP=2π√M4K=π√MK
- For mass Q (attached to spring constant K):
TQ=2π√MK
- From this, we can see that:
TQ=2TP
- This means the time period of Q is twice that of P.
- When Q is at its lowest point for the first time, it has completed half of its oscillation (downward motion).
- Since T_Q is twice T_P, it implies that while Q is at its lowest point, mass P would have completed its full oscillation (up and down).
- At the lowest point of its motion, the velocity of mass Q is zero (as it momentarily stops before changing direction).
- The velocity of mass P at this moment can be determined by its motion characteristics. Since P oscillates faster, it would be at its mean position when Q is at its lowest point.
- The velocity of mass P at its mean position is at its maximum.
- The maximum speed vmax for a mass in SHM is given by:
vmax=ωA
- Where ω=2πT and A is the amplitude of oscillation.
- Since Q is at its lowest point (velocity = 0) and P is at its mean position (velocity = maximum), the velocity of the image of Q in the mirror of block P with respect to the ground is equal to the velocity of P.
- Therefore, the velocity of the image of Q is equal to the velocity of P.
The velocity of the image of Q in the plane mirror of block P with respect to the ground when Q is at the lowest point for the first time is equal to the maximum velocity of mass P.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.32
Explore 9 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.33
Explore 20 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.30
Explore 9 Videos
- CURRENT ELECTRICITYBook:RESONANCE ENGLISHChapter:CURRENT ELECTRICITYExercise:High Level Problems (HIP)
Explore 19 Videos
- ELECTRO MAGNETIC WAVESBook:RESONANCE ENGLISHChapter:ELECTRO MAGNETIC WAVESExercise:Exercise 3
Explore 27 Videos
Similar Questions
Velocity of image of fish in the mirror with respect to ground is
View SolutionFind the velocity of the image when a plane mirror and a person are moving towards each other with same velocity v.
View Solution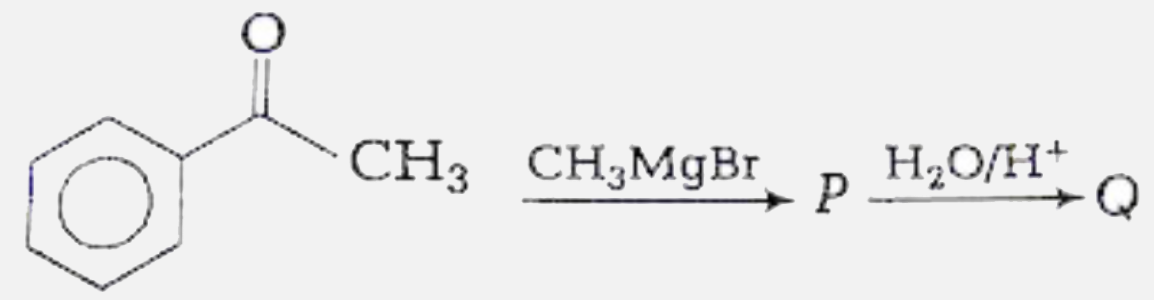
In the above reaction , P and Q respectively are
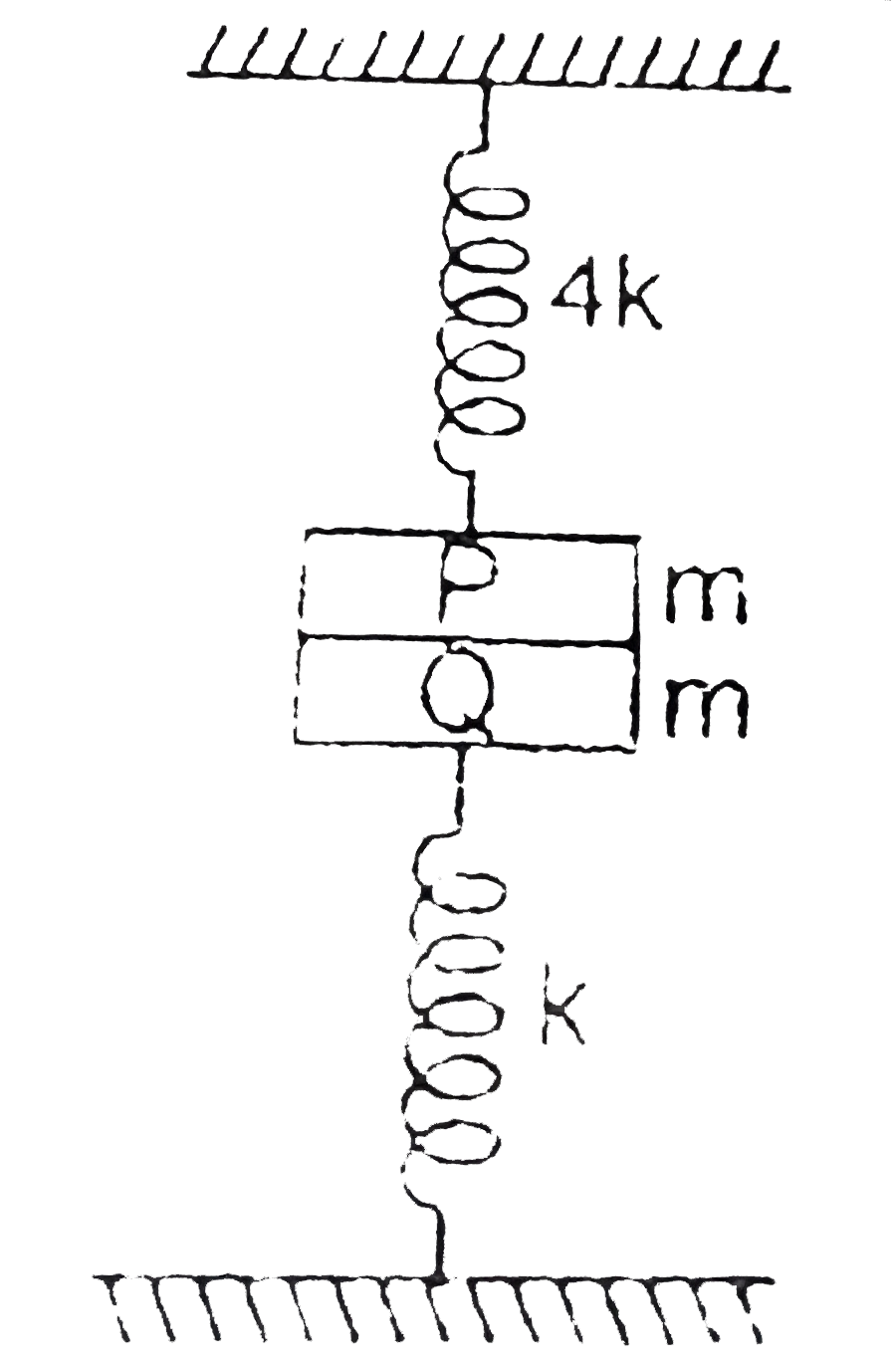
View SolutionIn the figure shown, blocks P and Q are in contact but do not stick to each other. The lower face of P behaves as a plane mirror. The springs are in their natural lengths. The system is released from rest. Then the distance between P and Q when Q is at the lowest point first time will be
View SolutionFind the image of the point (3,8)with respect to the line x+3y=7assuming the line to be a plane mirror.
View SolutionFind the image of the point (3,8)with respect to the line x+3y=7assuming the line to be a plane mirror.
View SolutionIf the image of the point (-4, 3, -5) in XZ-plane is
Q then the coordinates of Q is
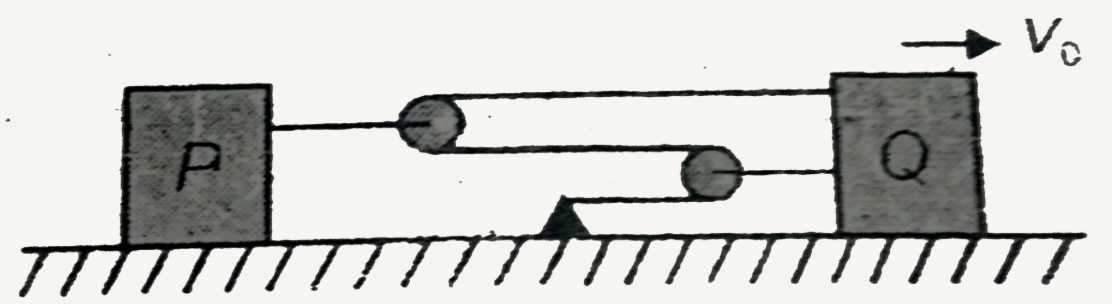
View SolutionThe block Q moves to the right with a constant velocity v0 as shown in figure. The relatives velocity of body P with respect to Q is ( assume all pulleys and strings are ideal)
View SolutionA person wants to see AB part of his image. His eye level is at 1.8m above the ground. If he uses minimum size of mirror required for this, find the height of the lowest point of mirror above the ground.
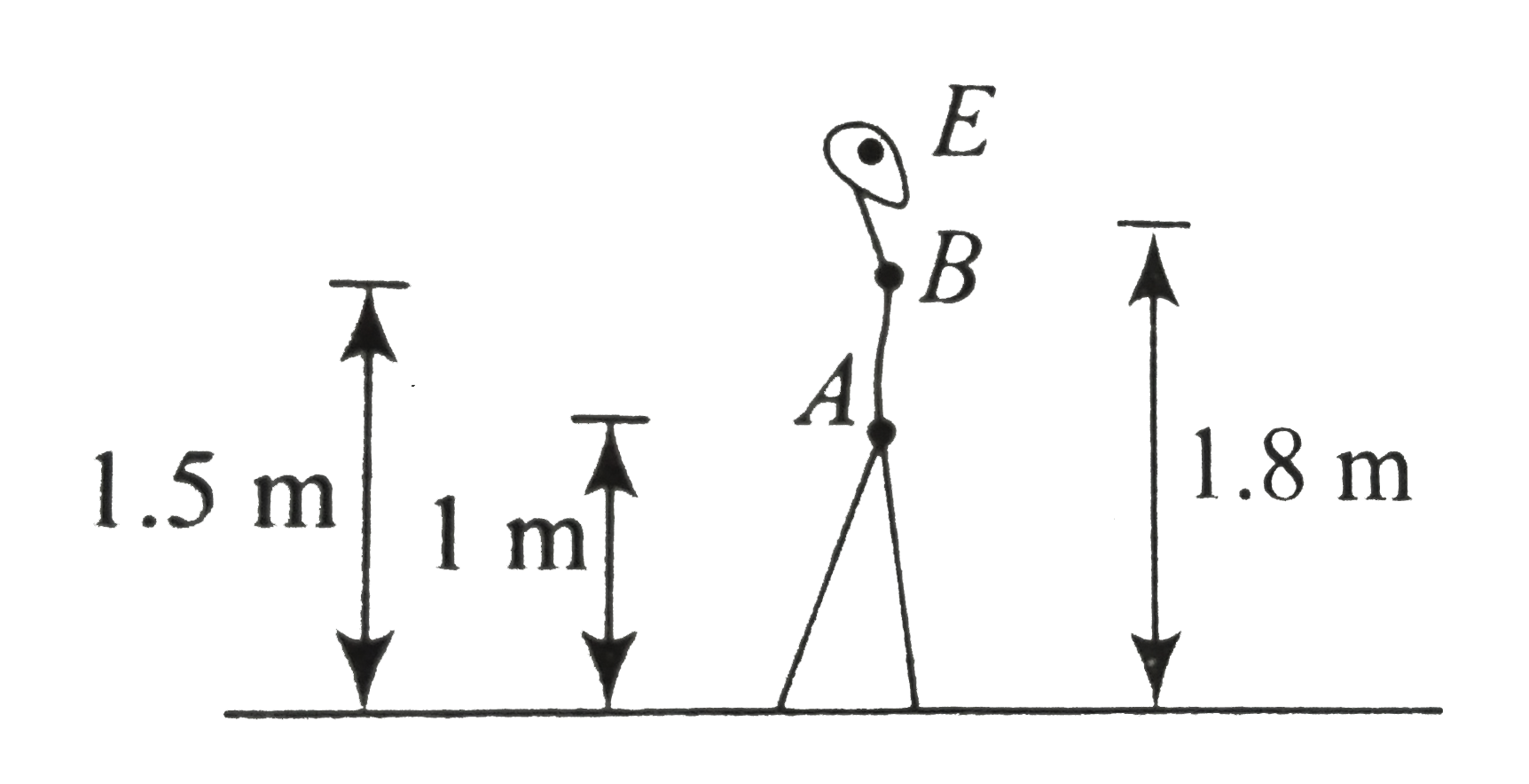
View SolutionQ is the image of point P(1, -2, 3) with respect to the plane x−y+z=7. The distance of Q from the origin is.
View Solution