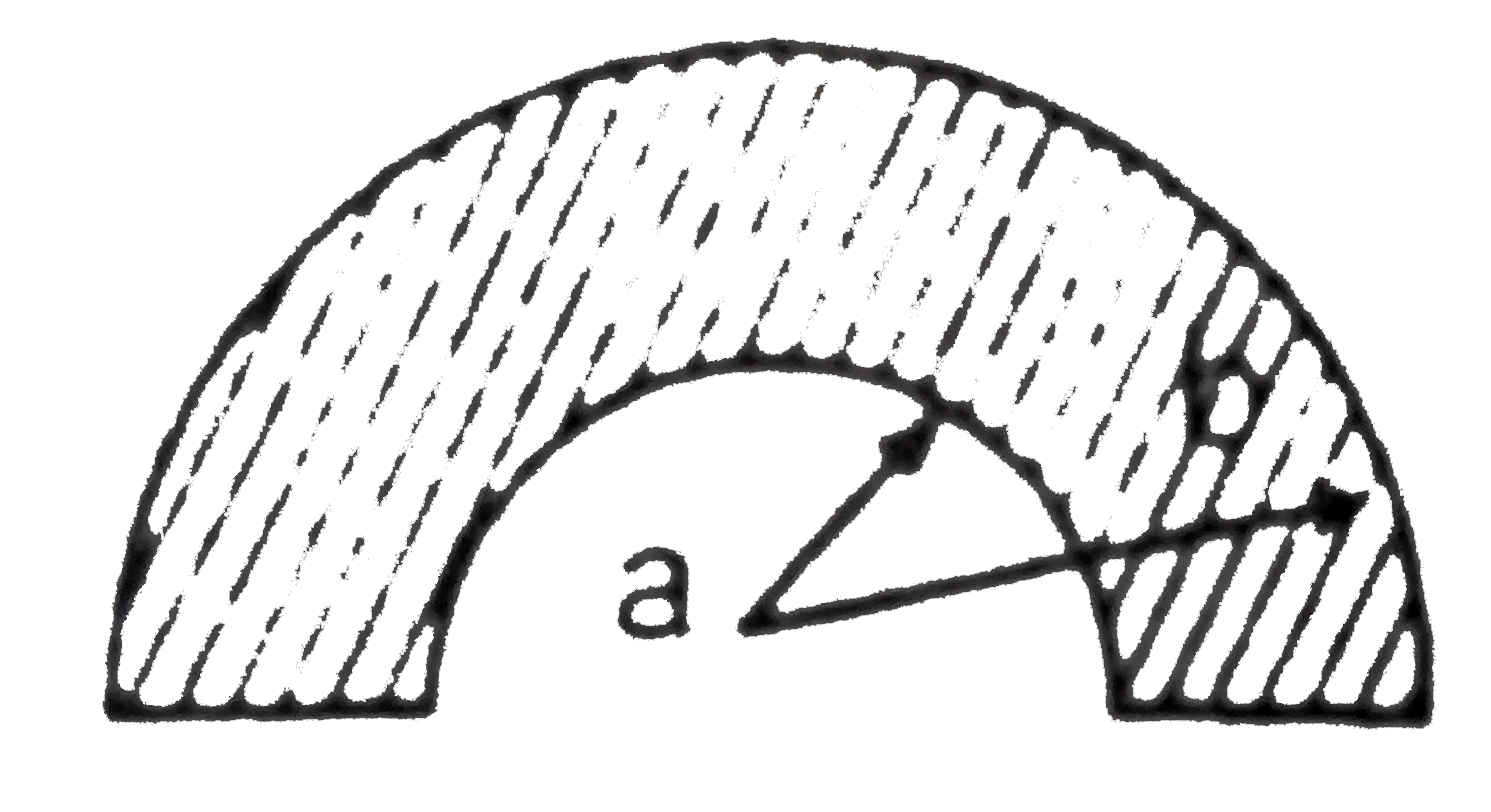
A non-conducting semi circular disc (as shown in figure) has a uniform surface charge density σ. The ratio of electric field to electric potential at the centre of the disc will be
1πlnb/a(b−a)
2π
1πln(b/a)2(b−a)
π(b−a)2ln(b/a)
The correct Answer is:C
E=∫dE=b∫x=a2Kσdxx=2Kσlnba
V=∫dv=b∫x=1Kπxσdxx=Kσπ(b−a)
⇒EV=2kσln(b/a)kσπ(b−a)=ln(b/a)2π(b−a).
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.32
9 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.33
20 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.30
9 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
19 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
Knowledge Check
Consider a thin spherical shell of radius R consisting of uniform surface charge density σ. The electric field at a point of distance x from its centre and outside the shell is
Ainversely proportional to σBdirectly proportional to x2Cdirectlr proportional to RDinversely proportional to x2
The electric field near a conducting surface having a uniform surface charge denstiy σ is given by
View Solution
The quarter disc of radius R (see figure) has a uniform surface charge density σ.
(a) Find electric potential at a point (O,O,Z)
(b). Find the Z component of electrif field at (O,O,Z)
View SolutionFind the electric field on the axis of a charged disc.
View SolutionThe surface density on a copper sphere is σ. The electric field strength on the surface of the sphere is
View Solution
An infinity long cylinder of radius R has an infinitely long cylindrical cavity of radius R2 are shown in the figure. The remaining portion has uniform volume charge density ρ. The magnitude of electrical field at the centre of the cavity is-
View SolutionTwo thin infinite parallel plates have uniform charge densities +σ and −σ. The electric field in the space between them is
View SolutionTwo infinite, non-conducting sheets of charge are parallel to each other, as shown in figure. The sheet on the left has a uniform surface charge density σ, and the one on the right has a uniform charge density −σ. Calculate the electric field at points (a) to the left of, (b) in between, and (c) to the right of the two sheets.

View Solution
