Find the electric field on the axis of a charged disc.
To find the electric field on the axis of a charged disc, we can follow these steps:
Step 1: Define the Problem
We have a charged disc with uniform surface charge density σ and radius R. We want to find the electric field at a point P located at a distance x from the center of the disc along its axis.
Step 2: Consider an Elemental Ring
To find the electric field, we consider an elemental ring of radius r and thickness dr on the disc. The area of this ring is given by:
dA=2πrdr
Step 3: Calculate Charge on the Elemental Ring
The charge dq on this elemental ring can be calculated as:
dq=σ⋅dA=σ⋅(2πrdr)
Step 4: Determine the Electric Field Due to the Elemental Ring
The electric field dE produced by this elemental ring at point P can be expressed as:
dE=14πϵ0⋅dqr2+x2⋅cos(θ)
where θ is the angle between the axis and the line connecting the ring to point P. The cosine of this angle is given by:
cos(θ)=x√r2+x2
Thus, we can write:
dE=14πϵ0⋅σ⋅(2πrdr)r2+x2⋅x√r2+x2
Step 5: Simplify the Expression
Substituting dq into the equation for dE:
dE=σ2ϵ0⋅x⋅rdr(r2+x2)3/2
Step 6: Integrate Over the Entire Disc
To find the total electric field E at point P, we need to integrate dE from r=0 to r=R:
E=∫R0dE=∫R0σ2ϵ0⋅x⋅rdr(r2+x2)3/2
Step 7: Change of Variables
Let t=r2+x2, then dt=2rdr or rdr=dt2. The limits change from r=0 (where t=x2) to r=R (where t=R2+x2):
E=σx4ϵ0∫R2+x2x21t3/2dt
Step 8: Evaluate the Integral
The integral ∫1t3/2dt evaluates to:
−2⋅1√t
Thus, we have:
E=σx4ϵ0(−2(1√R2+x2−1√x2))
This simplifies to:
E=σ2ϵ0(1−x√R2+x2)
Final Result
The electric field on the axis of a charged disc is given by:
E=σ2ϵ0(1−x√R2+x2)
We have a charged disc with uniform surface charge density σ and radius R. We want to find the electric field at a point P located at a distance x from the center of the disc along its axis.
To find the electric field, we consider an elemental ring of radius r and thickness dr on the disc. The area of this ring is given by:
dA=2πrdr
The charge dq on this elemental ring can be calculated as:
dq=σ⋅dA=σ⋅(2πrdr)
The electric field dE produced by this elemental ring at point P can be expressed as:
dE=14πϵ0⋅dqr2+x2⋅cos(θ)
where θ is the angle between the axis and the line connecting the ring to point P. The cosine of this angle is given by:
cos(θ)=x√r2+x2
Thus, we can write:
dE=14πϵ0⋅σ⋅(2πrdr)r2+x2⋅x√r2+x2
Substituting dq into the equation for dE:
dE=σ2ϵ0⋅x⋅rdr(r2+x2)3/2
To find the total electric field E at point P, we need to integrate dE from r=0 to r=R:
E=∫R0dE=∫R0σ2ϵ0⋅x⋅rdr(r2+x2)3/2
Let t=r2+x2, then dt=2rdr or rdr=dt2. The limits change from r=0 (where t=x2) to r=R (where t=R2+x2):
E=σx4ϵ0∫R2+x2x21t3/2dt
The integral ∫1t3/2dt evaluates to:
−2⋅1√t
Thus, we have:
E=σx4ϵ0(−2(1√R2+x2−1√x2))
This simplifies to:
E=σ2ϵ0(1−x√R2+x2)
The electric field on the axis of a charged disc is given by:
E=σ2ϵ0(1−x√R2+x2)
Similar Questions
A ring of radius a contains a charge q distributed. uniformly ober its length. Find the electric field at a point. on the axis of the ring at a distance x from the centre.
View SolutionThe surface charge density of a thin charged disc of radius R is σ. The value of the electric field at the centre of the disc σ2∈0. With respect to the field at the centre, the electric field along the axis at a distance R from the centre of the disc is
View Solution3 charges are placed in a circle of radius d as shown in figure. Find the electric field along x-axis at centre of circle.

View Solution3 charges are placed in a circle of radius d as shown in figure. Find the electric field along x-axis at centre of circle.

View SolutionA point charge is taken from a point A to a pint B in an electric field. Does the work done by the electric field depend on the path of the charge ?
View Solutionfind the electric field strength due to a point charge of 5μC at a distance of 80 cm from the charge.
View SolutionA charge q kept in front of a neutral metallic sphere. Find the electric field at the centre of sphere due to the induced charges on the surface of the sphere shown.
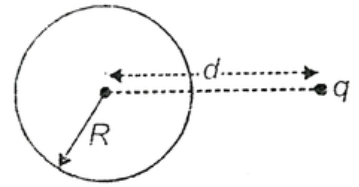
Strategy : The net electric field inside the conductor is zero. This is produced by induced charges and the external charge.
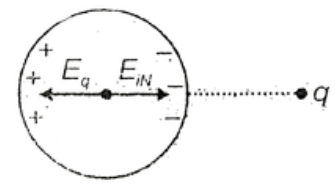
View SolutionA charge q kept in front of a neutral metallic sphere. Find the electric field at the centre of sphere due to the induced charges on the surface of the sphere shown.

Strategy : The net electric field inside the conductor is zero. Thsi is produced by induced charges and the external charge.

View SolutionFind the electric field caused by a disc of radius a with a uniform surfce charge density σ (charge per unit area) at a point along the axis of the disc a distance x from its centre.
View SolutionFind the electric field at the centre of a uniformly charged semicircular ring of radius R. Linear charge density is λ
View Solution