A conducting disc of radius R is placed in a uniform and constant magnetic field B parallel to the axis of the disc.With what angular speed should the disc be rotated about its axis such that no electric field develops in the disc (the electric charge and mass are e and m)
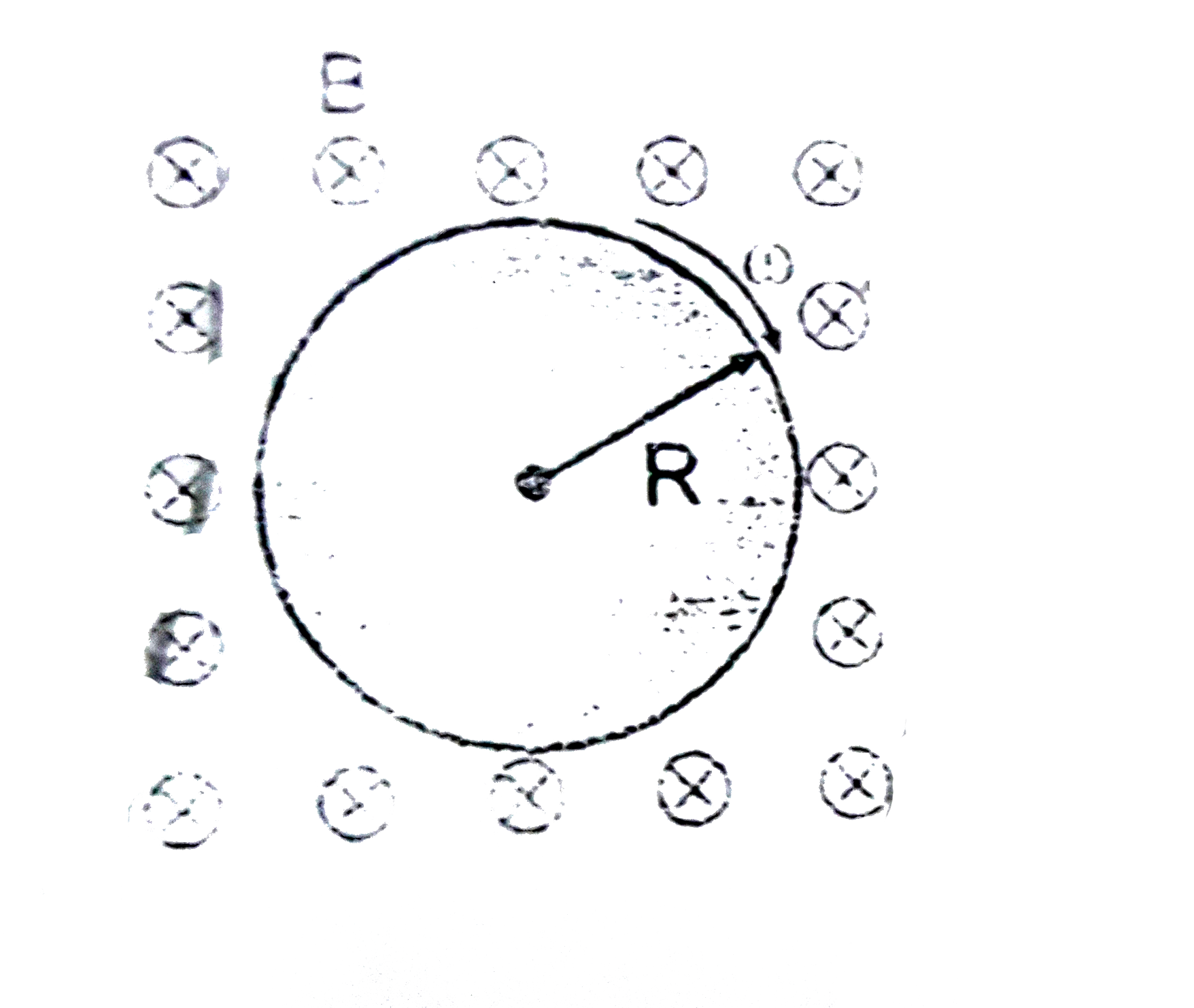
eB2m
eBm
2πmeB
πmeB
The correct Answer is:B
Consider a free electron in the disc at point P distant x from centre of disc.The magnetic force on free electron is =evB=eωxB(towards left) Centrifugal force=mω2x(towards right) For net force on the electron at P at be zero
i.e. eωxB=mω2x
or ω=eBm
There shall be no flow of free electrons radially outwards and hence no electric field shall develop

Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercis-2 PART 2
17 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercis-2 PART 3
10 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercis-1 PART 2
51 Videos
- ELECTRODYNAMICSBOOK - RESONANCECHAPTER - ELECTRODYNAMICSEXERCISE - Advanced level problems
31 Videos
- ELECTROSTATICSBOOK - RESONANCECHAPTER - ELECTROSTATICSEXERCISE - HLP
39 Videos
Similar Questions
Find the electric field on the axis of a charged disc.
View SolutionA conducting disc of radius r rotates with a small but constant angular velocity ω about its axis. A uniform magnetic field B exists parallel to the axis of rotation. Find the motional emf between the centre and the periphery of the disc.
View Solution
Knowledge Check
A brass disc is rotating about its axis. If temperature of disc is increased then its
Aradius of gyration increases, but moment of inertia remains the sameBmoment of inertia increases but radius of gyration remains the sameCradius of gyration, moment of inertia both remain the sameDradius of gyration, moment of inertia both increaseA uniform disc of mass M and radius R is hinged at its centre C. A force F is applied on the disc as shown. At this instant, the angular acceleration of the disc is
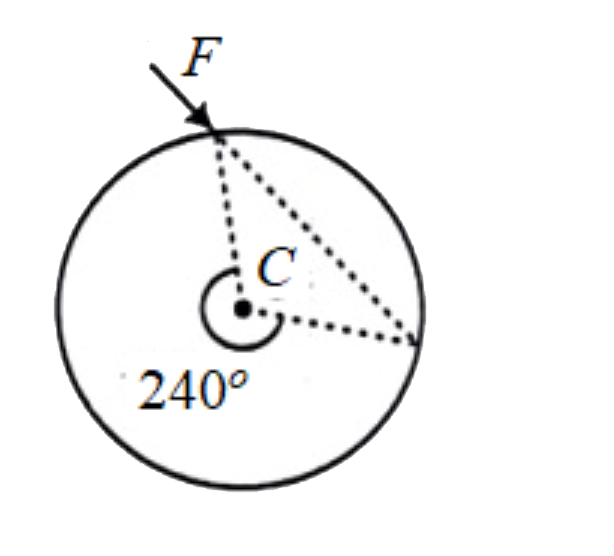 A√3FMRBFMRC2√3FMRDF2MR
A√3FMRBFMRC2√3FMRDF2MRWhen a circular disc of radius 0.5 m is rotating about its own axis, then the direction of its angular momentum is
Aalong the tangent drawn at every pointBradialCperpendicular to the direction of angular velocityDalong the axis of rotation of the body
A non-conducting thin disc of radius R charged uniformly over one side with surface density σ, rotates about its axis with an angular velocity ω. Find (a) the magnetic field induction at the centre of the disc (b) the magnetic moment of the disc.
View SolutionA uniform disc of mass M and radius R is hinged at its centre C . A force F is applied on the disc as shown . At this instant , angular acceleration of the disc is

View SolutionA non-conducting thin disc of radius R and mass m having charge uniformly over one side with surface density σ rotates about its axis with an angular velocity ω. Find :
(a) the magnetic induction at the centre of the disc,
(b) the magnetic moment of the disc.
( c) the ratio of magnetic moment and angular momentum of disc.
View SolutionA quarter disc of radius R and mass m is rotating about the axis OO' (perpendicular to the plane of the disc) as shown. Rotational kinetic energy of the quarter disc is

View Solutiona conducting disc of radius R roatates about its axis when an angular velocity ω.Then the potential difference between the centre of the disc and its edge is (no magnetic field is present ):
View Solution
