Find the electric potential at the axis of a uniformly charged disc and use potential to find the electric field at same point.
To find the electric potential at the axis of a uniformly charged disc and then use that potential to find the electric field at the same point, we can follow these steps:
Step 1: Define the Problem
We have a uniformly charged disc with surface charge density σ. We want to find the electric potential V at a point P located along the axis of the disc at a distance x from its center.
Step 2: Consider a Differential Element
Consider a small ring of radius r and thickness dr on the disc. The area of this ring is given by:
dA=2πrdr
The charge dQ on this ring is:
dQ=σdA=σ⋅2πrdr
Step 3: Calculate the Potential Due to the Ring
The potential dV at point P due to the small ring is given by the formula:
dV=kdQ√r2+x2
where k=14πϵ0.
Substituting dQ:
dV=k⋅σ⋅2πrdr√r2+x2
Step 4: Integrate to Find Total Potential
To find the total potential V at point P, we integrate dV from r=0 to r=R (the radius of the disc):
V=∫R0k⋅σ⋅2πrdr√r2+x2
Step 5: Solve the Integral
To solve the integral, we can use the substitution t=r2+x2, which gives dt=2rdr. Thus, rdr=12dt.
When r=0, t=x2 and when r=R, t=R2+x2.
The integral becomes:
V=k⋅σ⋅π∫R2+x2x2dt√t=k⋅σ⋅π(2√t)R2+x2x2
Calculating this gives:
V=k⋅σ⋅π(2√R2+x2−2√x2)
V=2k⋅σ⋅π(√R2+x2−x)
Step 6: Substitute k
Substituting k=14πϵ0:
V=σ2ϵ0(√R2+x2−x)
Step 7: Find the Electric Field
The electric field E at point P can be found using the relationship:
E=−dVdx
Differentiating V with respect to x:
E=−σ2ϵ0(x√R2+x2−1)
Final Expressions
Thus, the electric potential V at the axis of the uniformly charged disc is:
V=σ2ϵ0(√R2+x2−x)
And the electric field E at the same point is:
E=σ2ϵ0(1−x√R2+x2)
We have a uniformly charged disc with surface charge density σ. We want to find the electric potential V at a point P located along the axis of the disc at a distance x from its center.
Consider a small ring of radius r and thickness dr on the disc. The area of this ring is given by:
dA=2πrdr
The charge dQ on this ring is:
dQ=σdA=σ⋅2πrdr
The potential dV at point P due to the small ring is given by the formula:
dV=kdQ√r2+x2
where k=14πϵ0.
dV=k⋅σ⋅2πrdr√r2+x2
To find the total potential V at point P, we integrate dV from r=0 to r=R (the radius of the disc):
V=∫R0k⋅σ⋅2πrdr√r2+x2
To solve the integral, we can use the substitution t=r2+x2, which gives dt=2rdr. Thus, rdr=12dt.
V=k⋅σ⋅π∫R2+x2x2dt√t=k⋅σ⋅π(2√t)R2+x2x2
Calculating this gives:
V=k⋅σ⋅π(2√R2+x2−2√x2)
V=2k⋅σ⋅π(√R2+x2−x)
Substituting k=14πϵ0:
V=σ2ϵ0(√R2+x2−x)
The electric field E at point P can be found using the relationship:
E=−dVdx
Differentiating V with respect to x:
E=−σ2ϵ0(x√R2+x2−1)
Thus, the electric potential V at the axis of the uniformly charged disc is:
V=σ2ϵ0(√R2+x2−x)
And the electric field E at the same point is:
E=σ2ϵ0(1−x√R2+x2)
Topper's Solved these Questions
- ELECTROSTANTICSBOOK - FIITJEECHAPTER - ELECTROSTANTICSEXERCISE - MATRIX MATCH TYPE
1 Video
- ELECTROSTANTICSBOOK - FIITJEECHAPTER - ELECTROSTANTICSEXERCISE - ASSERTION REASONING TYPE
1 Video
- ELECTROMAGNETIC WAVE & WAVE OPTICSBOOK - FIITJEECHAPTER - ELECTROMAGNETIC WAVE & WAVE OPTICSEXERCISE - ASSIGNMENT PROBLEMS Objective : Level-II (MULTI CHOICE SINGLE CORRECT)
21 Videos
- ELECTROSTATICSBOOK - FIITJEECHAPTER - ELECTROSTATICSEXERCISE - Example
14 Videos
Similar Questions
Knowledge Check
The electric field at the centre of a uniformly charged ring is zero. What is the electric field and potential at the centre of a half ring if the charge on it be Q and its radius be R?
A14πε0QπR2,14πε0QπRB14πε0QR2,14πε02QπRC14πε02QπR2,14πε0QRD14πε02QR2,14πε03QπRA charge +Q at A (see figure) produces electric field E and electric potential V at D. If we now put charges −2Q and +Q at B and C respectively, then the electric field and potential at D will be
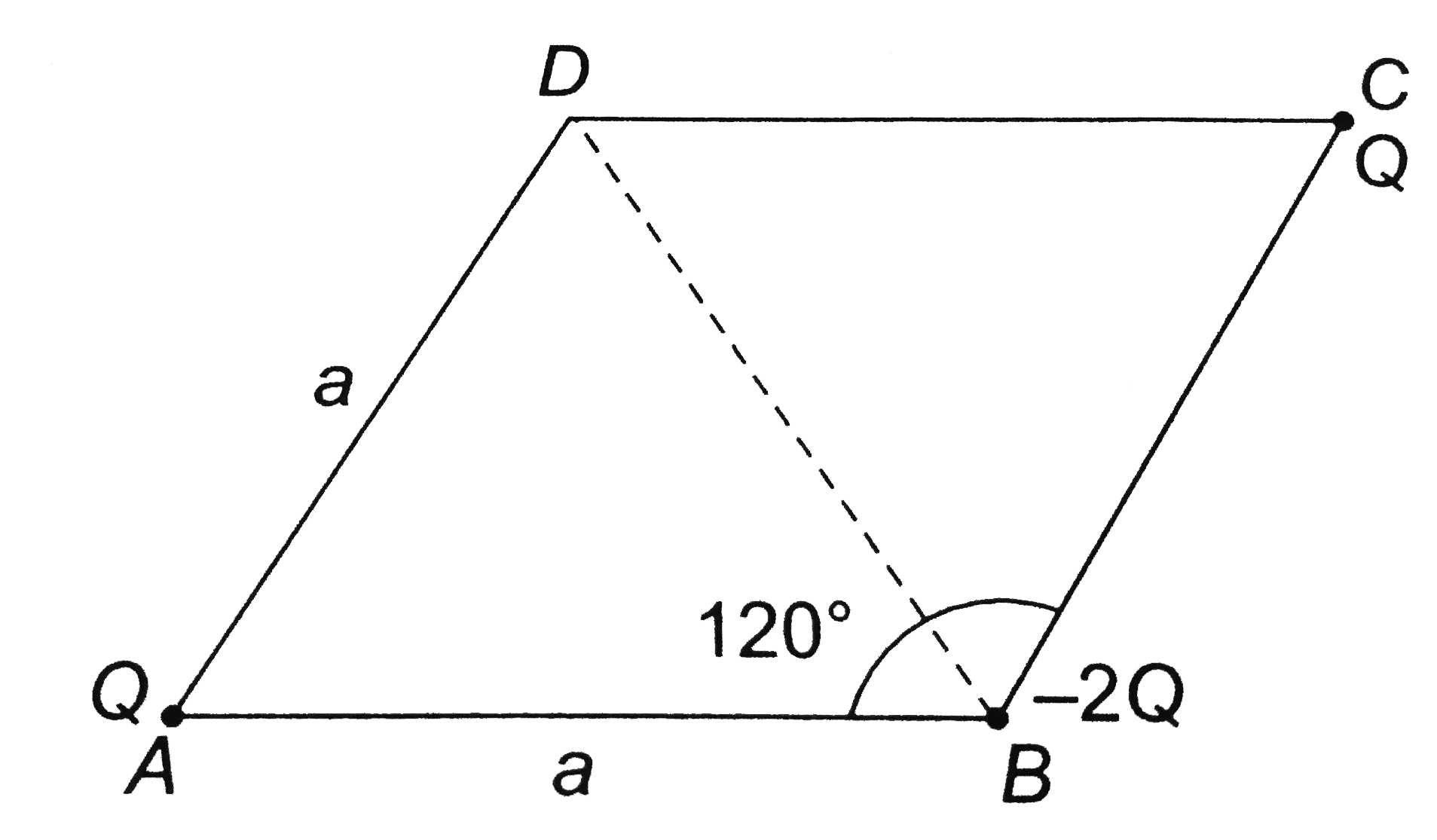 AE and 0B0 and VC√2E and V√2DE√2 and V√2
AE and 0B0 and VC√2E and V√2DE√2 and V√2For an electric dipole potential & electric field
Acan have same magnitude for a point at a distance less than 2 meterBcan have same magnitude fo a point at distacnes greater than 2 meterCcan never be equalDcan never be predicted
Find the electric potential energy of a unifomly charged then spherical shell.
View SolutionFind the electric potential energy of the system of charges.
(a)
View SolutionFind the electric field on the axis of a charged disc.
View SolutionFind the electric field due to an uniformly charged arc, at the center 'c'.

View SolutionA charge Q is uniformly on a ring of radius R. Find the electric potential on the axis of ring at distance x from the centre of the ring. Sketch variation of potential with respect to x.
View Solution