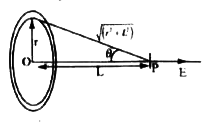
A ring of radius a contains a charge q distributed. uniformly ober its length. Find the electric field at a point. on the axis of the ring at a distance x from the centre.

shows the situation. Let us consider a
. small element of the ring at the point A having a charge
. dQ. The field at P due to this element is
.
By symmmetry, the field at P will be along the exis OP
. The comonent of dE along this direction is.
The net field at P is
.
Topper's Solved these Questions
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - worked out Examples
19 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Exercises
75 Videos
- ELECTRIC CURRENT THROUGH GASESBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Short answer
6 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Questions for short answer
9 Videos
Similar Questions
Mass of 1 kg is distributed uniformly over a ring of radius 1m. Find the gravitational potential at a point lies on the axis of the ring at a distance of 1m from the centre.
View SolutionMass of 20 kg is distributed uniformly over a ring of radius 2m. Find the the grvitational field at a point lies an th axis of the ring at a distance of 2√3 m from the centre.
View SolutionA thin wire of radius ..r.. carries a charge q. Find the magnitude of the electric field strength on the axis of the ring as a function of distance L from the centre. Find the same for L>>r Find maximum field strength and the corresponding distance L.
View SolutionA ring of radius R is having two charges q and 2q distributed on its two half parts. The electric potentiasl at a point on its axis at a distance of 2√2R from its centre is (k=14πε0)
View SolutionElectric charge Q is uniformly distributed around a thin ring of radius a. find the potential a point P on the axis of the ring at a distance x from the centre of the ring .

View SolutionA point charge q is located at the centre fo a thin ring of radius R with uniformly distributed charge −q, find the magnitude of the electric field strength vectro at the point lying on the axis of the ring at a distance x from its centre, if x>>R.
View SolutionA charge is distributed uniformly over a ring of radius 'a'. Obtain an expression for the electric intensity E at a point on the axis of the ring . Hence show that for points at large distances from the ring it behaves like a point charge .
View SolutionA ring of radius R carries a uniformly distributed charge +Q. A point charge −q is placed on the axis of the ring at a distance 2R from the centre of the ring and released from rest. The particle executes a simple harmonic motion along the axis of the ring. State True or False.
View SolutionA thin semi-circular ring of radius r has a positive charge q distributed uniformly over it. The net field →E at the centre O is
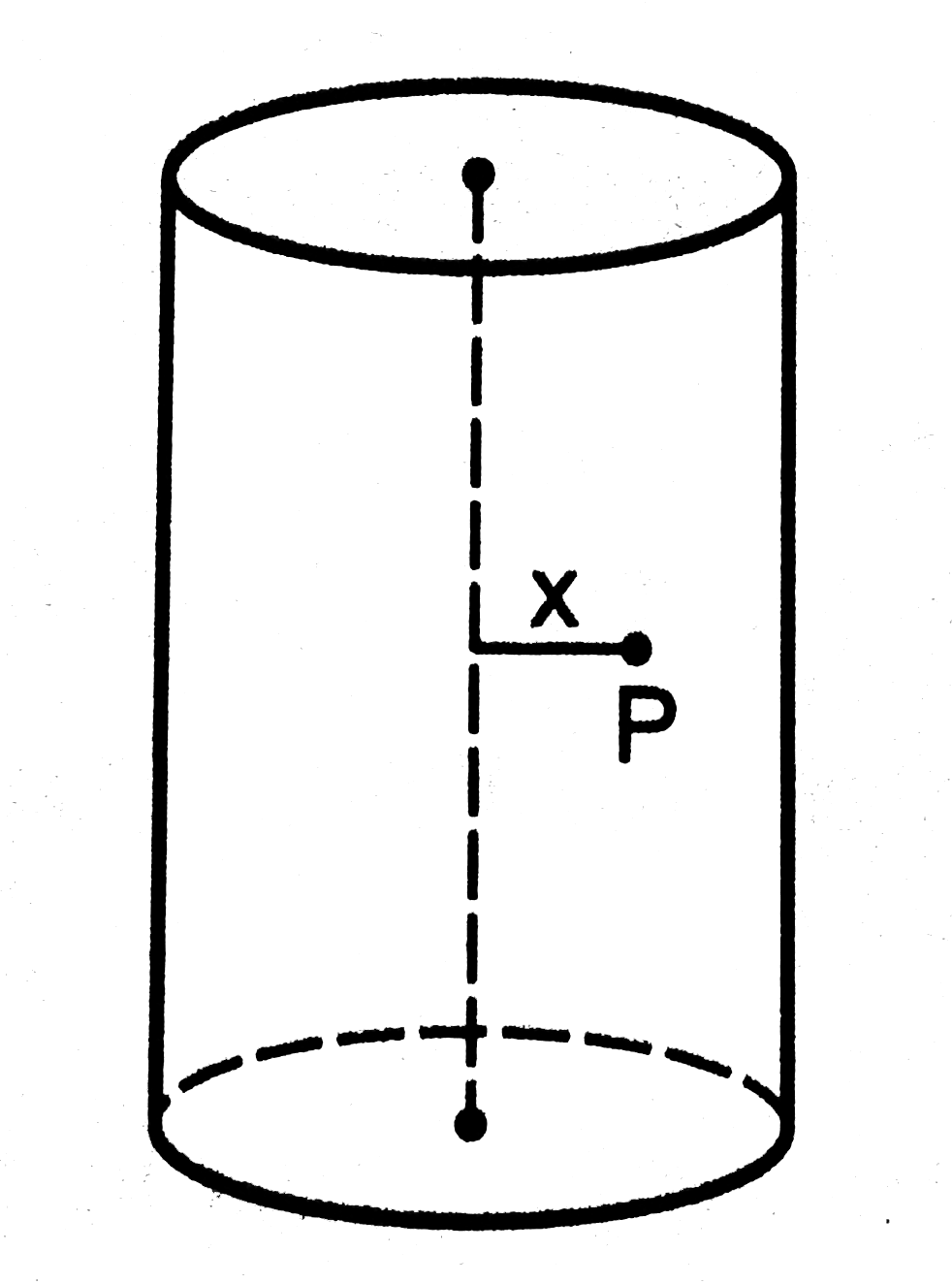
View SolutionA long cylindrical volume contains a uniformly distributed charge of density ρ. Find the electric field at a point P inside the cylindrical volume at a distance x from its axis (figure 30-E5) ,
View Solution
