A point charge q is located at the centre fo a thin ring of radius R with uniformly distributed charge −q, find the magnitude of the electric field strength vectro at the point lying on the axis of the ring at a distance x from its centre, if x>>R.
QR28πε0x4
3QR28πε0x4
5QR28πε0x4
7QR28πε0x4
The correct Answer is:B

Electric field due to uniformly charged Ring at it's axis (at distance x) =−KQx(R2+x2)3/2
and Electric field due to point charge =KQx2
So net electric field =KQx2+−KQx(R2+x2)3/2=KQ[(R2+x2)3/2−x3]x2[R2+x2]3/2
When Rlt lt x=KQ[1+3R22x2−1]x2[1]=3KQR22x4=−3QR28πε0x4
Related Playlists
Similar Questions
A charge q is uniformly distributed over a quarter circular ring of radius r. The magnitude of electric field strength at the centre of the ring will be
View SolutionA ring of radius a contains a charge q distributed. uniformly ober its length. Find the electric field at a point. on the axis of the ring at a distance x from the centre.
View SolutionElectric charge Q is uniformly distributed around a thin ring of radius a. find the potential a point P on the axis of the ring at a distance x from the centre of the ring .
 View Solution
View SolutionCharge q is uniformly distributed over a thin half ring of radius R. The electric field at the centre of the ring is
View SolutionA thin nonconducting ring of radius R has a linear charge density λ=λ0cosφ, where λ0 is a constant , ϕ is the azimuthal angle. Find the magnitude of the electric field strength
(a) at the centre of the ring ,
(b) on the axis of the ring as a function of the distance x from its centre. Investegation the obtained function at x>>R.View SolutionA thin wire of radius ..r.. carries a charge q. Find the magnitude of the electric field strength on the axis of the ring as a function of distance L from the centre. Find the same for L>>r Find maximum field strength and the corresponding distance L.
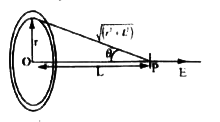 View Solution
View SolutionA point charge q is situated at a distance r from one end of a thin conduction rod of length L having a charge Q (uniformly distributed a long its length).find the magnitudes of electric force between the two.
View SolutionThree point charges -Q, Q and Q are placed on a straight line with distance d between charges as shown. Find the magnitude of the electric field at the point P in the configuration shown which is at a distance a from middle charge Q in the system provided that a>>d. Take 2Qd=p.
 View Solution
View SolutionA ring of radius R has charge −Q distributed uniformly over it. Calculate the charge that should be placed at the center of the ring such that the electric field becomes zero at apoint on the axis of the ring at distant R from the center of the ring.
View SolutionA nonconducting ring of radius R has uniformly distributed positive charge Q. A small part of the ring.of length d, is removed (d<<R). The electric field at the centre of the ring will now be
View Solution


