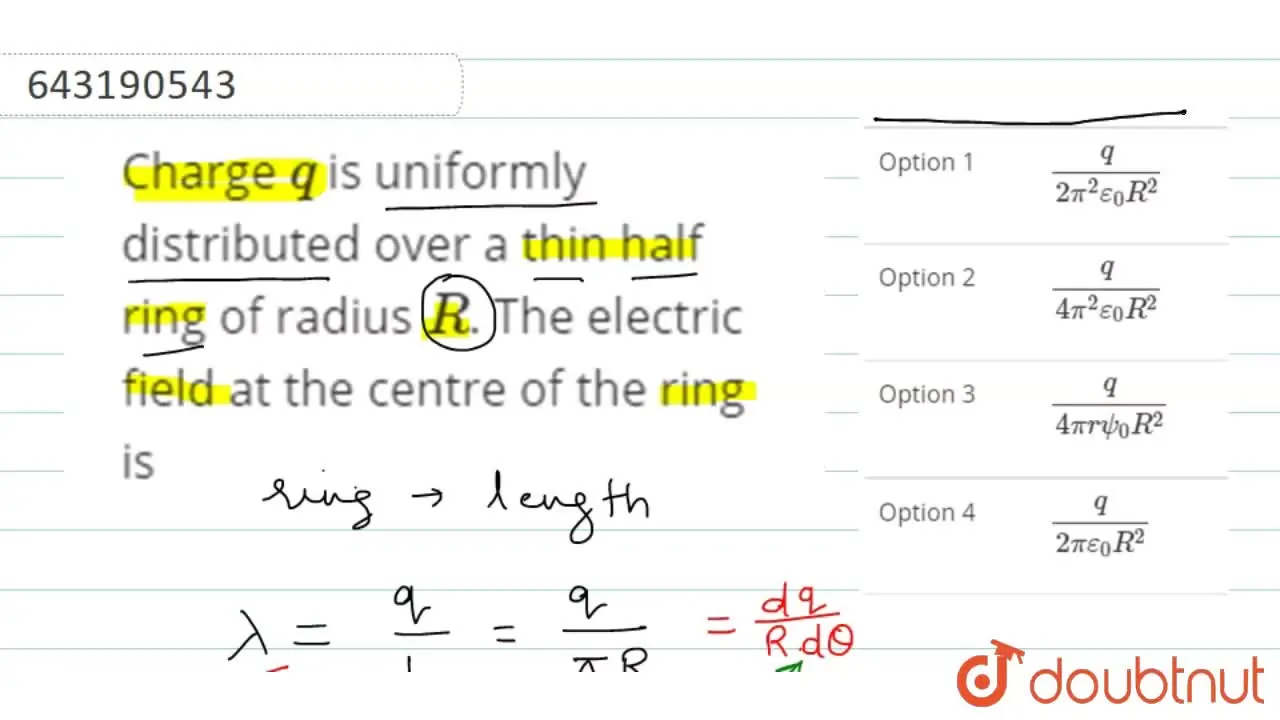
Charge q is uniformly distributed over a thin half ring of radius R. The electric field at the centre of the ring is
q2π2ε0R2
q4π2ε0R2
q4πrψ0R2
q2πε0R2
The correct Answer is:A
Step by step video & image solution for Charge q is uniformly distributed over a thin half ring of radius R. The electric field at the centre of the ring is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Assertion and Reason15videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Match the columns5videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Check point 1.520videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises50videos
ELECTROSTATIC POTENTIAL AND CAPACITORS
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions135videos
GRAVITATION
Similar Questions
A charge +Q is uniformly distributed over a thin ring of the radius R. The velocity of an electron at the moment when it passes through the centre O of the ring, if the electron was initially at far away on the axis of the ring is (m=mass of electron, K=14πε0)
View SolutionA thin glass rod is bent into a semicircle of radius r. A charge +Q is uniformly distributed along the upper half, and a charge -Q is uniformly distributed along the lower half, as shown in fig. The electric field E at P, the center of the semicircle, is
 View Solution
View SolutionA charge q is uniformly distributed over a quarter circular ring of radius r. The magnitude of electric field strength at the centre of the ring will be
View SolutionElectric charge Q is uniformly distributed around a thin ring of radius a. find the potential a point P on the axis of the ring at a distance x from the centre of the ring .
 View Solution
View SolutionA positive charge Q is uniformly distributed along a circular ring of radius R.a small test charge q is placed at the centre of the ring.
 View Solution
View SolutionA positive charge Q is uniformly distributed along a circular ring of radius R.a small test charge q is placed at the centre of the ring .The
 View Solution
View SolutionA wire of length l and charge q is bent in form of a semicircle. The charge is uniformly distributed over the length. The electric field at the centre of semicircle is
View SolutionA solid sphere of radius R has a spherical cavity of radius r as shown in the figure. If the volume charge density σ is uniformly distributed over the whole volume of the sphere, then electric field strength at the centre of the sphere will be
 View Solution
View SolutionA charge q is unifomly distrybuted over a nonconducting ring of radius R. The ring is rotated about an axis passing through its centre and perpendicular to the plane of the ring with frequency f. The ratio of electric potential to the magnetic field at the centre of the ring depends on.
View SolutionA nonconducting ring of radius R has uniformly distributed positive charge Q. A small part of the ring.of length d, is removed (d<<R). The electric field at the centre of the ring will now be
View Solution