A thin glass rod is bent into a semicircle of radius r. A charge +Q is uniformly distributed along the upper half, and a charge -Q is uniformly distributed along the lower half, as shown in fig. The electric field E at P, the center of the semicircle, is

Qπ2ε0r2
2Qπ2ε0r2
4Qπ2ε0r2
Q4π2ε0r2
The correct Answer is:A
Take PO as the x-axis and PA as the y-axis. Consider two elements EF and E'F' pf width dθ at angular θ above and below PO, respectively

The magnitude of the field at P due to either element is
dE=14πε0rdθ×Q/(πr/2)r2=Q2π2ε0r2dθ
Resolving the field we find that the components along PO sum up to zero, and hence the resultant fields is along PB. Therefore, field at P due to pair of elements is 2dEsinθ
E=∫π/202dEsinθ
=2∫π/20Q2πε0r2sinθdθQπ2ε0r2.
Topper's Solved these Questions
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Multiple Correct
8 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Comprehension
25 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Subjective
32 Videos
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type
51 Videos
- ELECTRIC CURRENT & CIRCUITSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits
15 Videos
Similar Questions
Charge q is uniformly distributed over a thin half ring of radius R. The electric field at the centre of the ring is
View SolutionA wire of length l and charge q is bent in form of a semicircle. The charge is uniformly distributed over the length. The electric field at the centre of semicircle is
View SolutionCalculate potential on the axis of a ring due to charge Q uniformly distributed along the ring of radius R.
View SolutionA spherical shell of radius R has a uniformly distributed charge ,then electric field varies as
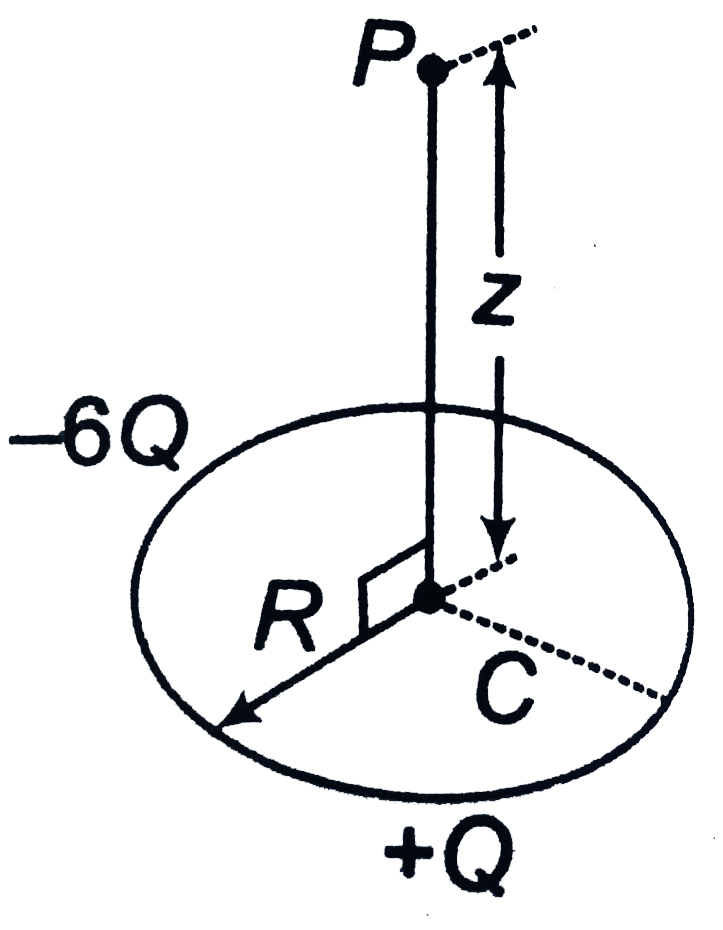
View SolutionA plastic rod has been formed into a circle of radius R. It has a positive charge +Q uniformly distributed along one-quarter of its circumference and a negative charge of −6Q uniformly distributed along the rest of the circumference (figure). With V = 0 at infinity, what is the electric potential −6Q
(a) at the centre C of the circle and
(b) at point P, which is on the central axis of the circle at distance z from the centre?
View SolutionA charge q is uniformly distributed over a quarter circular ring of radius r. The magnitude of electric field strength at the centre of the ring will be
View SolutionA charge −Q is unformly distributed over a non-conducting semi-circular rod of radius R. The potential at the center is
View SolutionA positive charge Q is uniformly distributed along a circular ring of radius R.a small test charge q is placed at the centre of the ring.

View SolutionA positive charge Q is uniformly distributed along a circular ring of radius R.a small test charge q is placed at the centre of the ring .The

View SolutionCalculate electric field due to a charge uniformly distributed in a spherical volume
View Solution
