A spherical shell of radius R has a uniformly distributed charge ,then electric field varies as
inside is zero and varies as x−1 outside it
inside is non zero constant and varies as x2 outside it
inside is zero and varies as x−2 outside it
inside is constant and varies as x−1 outside it
The correct Answer is:C
To solve the problem regarding the electric field due to a uniformly charged spherical shell, we can follow these steps:
1. Understanding the Configuration:
We have a spherical shell of radius R with a uniformly distributed charge Q. We need to analyze the electric field at different points relative to the shell.
2. Electric Field Inside the Shell:
According to Gauss's Law, the electric field inside a uniformly charged spherical shell is zero. This is because the symmetry of the charge distribution leads to cancellation of the electric field vectors at any point inside the shell.
Einside=0forr<R
3. Electric Field on the Surface of the Shell:
At the surface of the shell (where r=R), we can use Gauss's Law to find the electric field. The electric field E at the surface can be calculated as:
Esurface=14πϵ0⋅QR2
4. Electric Field Outside the Shell:
For points outside the shell (where r>R), the shell behaves like a point charge located at its center. Thus, the electric field at a distance r from the center is given by:
Eoutside=14πϵ0⋅Qr2
5. Summary of Electric Field Behavior:
- Inside the shell (r<R): E=0
- On the surface of the shell (r=R): E=14πϵ0⋅QR2
- Outside the shell (r>R): E=14πϵ0⋅Qr2
6. Conclusion:
The electric field varies as follows:
- It is zero inside the shell.
- It behaves inversely with the square of the distance outside the shell.
Final Answer:
The electric field varies as:
- E=0 for r<R
- E∝1r2 for r>R
We have a spherical shell of radius R with a uniformly distributed charge Q. We need to analyze the electric field at different points relative to the shell.
According to Gauss's Law, the electric field inside a uniformly charged spherical shell is zero. This is because the symmetry of the charge distribution leads to cancellation of the electric field vectors at any point inside the shell.
Einside=0forr<R
At the surface of the shell (where r=R), we can use Gauss's Law to find the electric field. The electric field E at the surface can be calculated as:
Esurface=14πϵ0⋅QR2
For points outside the shell (where r>R), the shell behaves like a point charge located at its center. Thus, the electric field at a distance r from the center is given by:
Eoutside=14πϵ0⋅Qr2
- Inside the shell (r<R): E=0
- On the surface of the shell (r=R): E=14πϵ0⋅QR2
- Outside the shell (r>R): E=14πϵ0⋅Qr2
The electric field varies as follows:
- It is zero inside the shell.
- It behaves inversely with the square of the distance outside the shell.
The electric field varies as:
- E=0 for r<R
- E∝1r2 for r>R
Topper's Solved these Questions
- ELECTROSTATICSBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - LEVEL - 2
60 Videos
- ELECTROSTATICSBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE MAIN
65 Videos
- ELECTROSTATICSBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - LEVEL - 0 (LONG ANSWER TYPE )
8 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT EXERCISE - IMPECCABLE
52 Videos
- ENERGY & MOMENTUMBOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE) - TRUE/FALSE TYPE
1 Video
Similar Questions
A spherical shell of radius R carries a uniformly distributed charge q. The electrical forces arising cause the ex-pansion of the shell. Find the mechanical stress in the shell.
View SolutionA charge Q is uniformly distributed in a dielectric sphere of radius R (having dielectric constant unity). This dielectric sphere is enclosed by a concentric spherical shell of radius 2R and having uniformly distributed charge 2Q. Which of the following graph correctly represents variation of electric field with distance r from the common centre?

View Solution
Knowledge Check
Consider a thin spherical shell of radius R consisting of uniform surface charge density σ. The electric field at a point of distance x from its centre and outside the shell is
Ainversely proportional to σBdirectly proportional to x2Cdirectlr proportional to RDinversely proportional to x2There is a solid sphere of radius R having uniformly distributed charge throughout it. What is the relation between electric field E and distance r from the centre (r is less than R) ?
AE∝r−2BE∝r−1CE∝rDE∝r2
A thin spherical shell radius of R has a charge Q uniformly distributed on it. At the centre of the shell, a negative point charge -q is placed. If the shell is cut into two identical hemispheres, still equilibrium is maintained. Then find the relation between Q and q?

View SolutionA spherical shell of radius R=1.5cm has a charge q=20μC uniformly distributed over it. The force exerted by one half over the other half is
View SolutionA hallow metal sphere of radius R is uniformly charged. The electric field due to the sphere at a distance r from the centre:
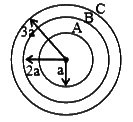
View SolutionThree concentric spherical shells A, B and C having uniformly distributed total charges +Q, -2Q and +Q respectively are placed as shown. The potential at the centre will be -
View SolutionA circular ring carries a uniformly distributed positive charge .The electric field(E) and potential (V) varies with distance (r ) from the centre of thr ring along its axis as

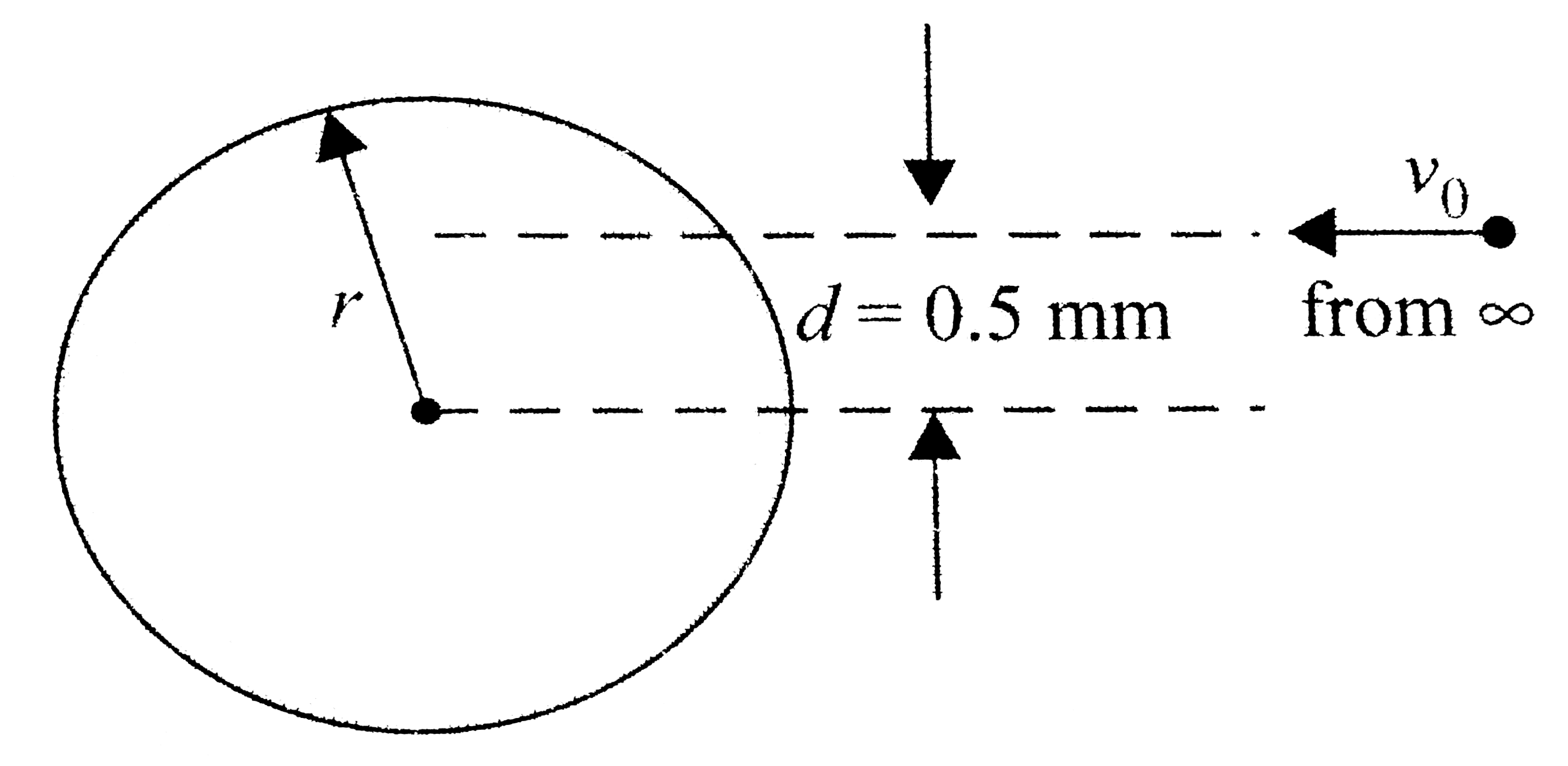
View SolutionA particle of mass 1kg and charge 1/3μC is projected toward a nonconducing fixed spherical shell of radius r=1mm having the same charge uniformly distributed on its surface. Find th minimum initial velocity of projection requires if the particle just grazes the shell.
 .
.
View Solution
