A particle of mass m and charge -q moves diametrically through a uniformily charged sphere of radius R with total charge Q. The angular frequency of the particle's simple harminic motion, if its amplitude lt R, is given by
√14πε0qQmR
√14πε0qQmR2
√14πε0qQmR3
√14πε0mqQ
The correct Answer is:C
To solve the problem of finding the angular frequency of a particle of mass m and charge −q moving diametrically through a uniformly charged sphere of radius R with total charge Q, we can follow these steps:
Step 1: Understand the System
The particle with charge −q is moving through a uniformly charged sphere with charge Q. The electric field inside a uniformly charged sphere is given by:
E=Qr4πϵ0R3
where r is the distance from the center of the sphere to the particle.
Step 2: Determine the Force on the Particle
The force F acting on the particle due to the electric field is given by:
F=qE
Substituting the expression for E:
F=−q(Qr4πϵ0R3)
This force acts towards the center of the sphere (since the charge of the particle is negative).
Step 3: Relate Force to Simple Harmonic Motion
The force can be expressed in a form similar to Hooke's law, which describes simple harmonic motion (SHM):
F=−kx
where k is the spring constant and x is the displacement from the equilibrium position. In our case, x=r (the distance from the center), and we can identify:
k=qQ4πϵ0R3
Step 4: Set Up the Equation for Angular Frequency
For SHM, the angular frequency ω is related to the mass m and the spring constant k by the equation:
k=mω2
Substituting our expression for k:
qQ4πϵ0R3=mω2
Step 5: Solve for Angular Frequency ω
Rearranging the equation gives:
ω2=qQ4πϵ0mR3
Taking the square root of both sides, we find:
ω=√qQ4πϵ0mR3
Final Answer
Thus, the angular frequency of the particle's simple harmonic motion is:
ω=√qQ4πϵ0mR3
---
The particle with charge −q is moving through a uniformly charged sphere with charge Q. The electric field inside a uniformly charged sphere is given by:
E=Qr4πϵ0R3
where r is the distance from the center of the sphere to the particle.
The force F acting on the particle due to the electric field is given by:
F=qE
Substituting the expression for E:
F=−q(Qr4πϵ0R3)
This force acts towards the center of the sphere (since the charge of the particle is negative).
The force can be expressed in a form similar to Hooke's law, which describes simple harmonic motion (SHM):
F=−kx
where k is the spring constant and x is the displacement from the equilibrium position. In our case, x=r (the distance from the center), and we can identify:
k=qQ4πϵ0R3
For SHM, the angular frequency ω is related to the mass m and the spring constant k by the equation:
k=mω2
Substituting our expression for k:
qQ4πϵ0R3=mω2
Rearranging the equation gives:
ω2=qQ4πϵ0mR3
Taking the square root of both sides, we find:
ω=√qQ4πϵ0mR3
Thus, the angular frequency of the particle's simple harmonic motion is:
ω=√qQ4πϵ0mR3
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Multiple Correct8videos
COULOMB LAW AND ELECTRIC FIELD
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Comprehension25videos
COULOMB LAW AND ELECTRIC FIELD
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Subjective32videos
COULOMB LAW AND ELECTRIC FIELD
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type51videos
CENGAGE PHYSICS DPP
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits15videos
ELECTRIC CURRENT & CIRCUITS
Similar Questions
A charged particle of mass m and charge q travels on a circular path of radius r that is perpendicular to a magnetic field B. The time takeen by the particle to complete one revolution is
View SolutionA bullet of mass m and charge q is fired towards a solid uniformly charge sphere of radius R and total charge +q. If it strikes the surface of sphere with speed u, find the minimum value of u so that it can penetrate through the sphere. (Neglect all resistance force or friction acting on bullet except electrostatic forces)
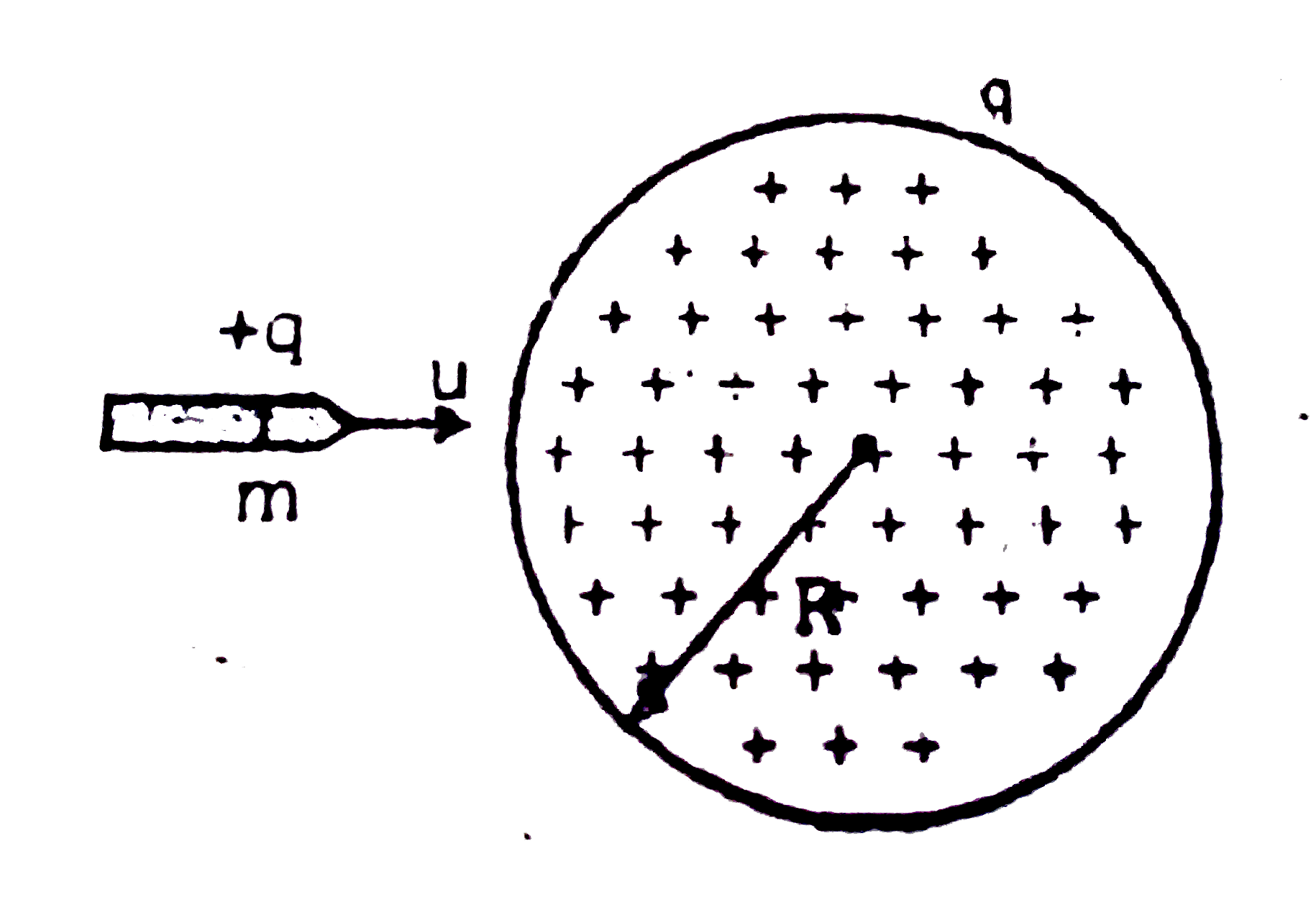 View Solution
View SolutionA particle of mass m and charge -q circulates around a fixed charge q in a circle radius under electrostatic force. The total energy of the system is (k= (14πε0))
View SolutionA charged particle of mass m and charge q describes circular motion of radius r in a uniform magnetic field of strength B the frequency of revolution is
View SolutionA uniformly charged solid sphere a mass M, radius R having charge Q is rotated about its diameter with frequency f0. The magnetic moment of the sphere is
View SolutionA particle having charge + q is fixed at a point O and a second particle of mass m and having charge −q0 moves with constant speed in a circle of radius r about the charge +q. the energy required to be supplied to the moving charge to increase radius of the path to 2r is qq0nπε0r. Find the value of n.
View SolutionFind out energy stored in the electric field of uniformly charged thin spherical shell of total charge Q and radius R.
View SolutionA conducting sphere of radius R and carrying a charge Q is joined to an uncharged conducting sphere of radius 2R. The charge flowing between them will be
View SolutionA particle of mass m and charge q is located midway between two fixed charged particles each having a charge q and a distance 2l apart. Prove that the motion of the particle will be SHM if it is displaced slightly along the line connecting them and released. Also find its time period.
View SolutionA charged particle of mass m and charge q is released from rest in an electric field of constant magnitude E. The kinetic energy of the particle after time t is
View Solution
