The maximum velocity at the lowest point, so that the string just slack at the highest point in a vertical circle of radius l.
√gl
√3gl
√5gl
√7gl
The correct Answer is:C
To solve the problem of finding the maximum velocity at the lowest point of a vertical circle such that the string just goes slack at the highest point, we can use the principles of conservation of energy and the dynamics of circular motion. Here’s a step-by-step solution:
Step 1: Understand the System
We have a mass moving in a vertical circle of radius L. At the lowest point, we denote the velocity as VL and at the highest point as VH. The goal is to find VL such that the tension in the string is zero at the highest point.
Step 2: Apply Conservation of Energy
Using the conservation of mechanical energy, we can equate the total mechanical energy at the lowest point and the highest point.
- At the lowest point (height = 0):
- Potential Energy (PE) = 0
- Kinetic Energy (KE) = 12mV2L
- At the highest point (height = 2L):
- Potential Energy (PE) = mg(2L)=2mgL
- Kinetic Energy (KE) = 12mV2H
Setting the total energy at the lowest point equal to the total energy at the highest point gives us:
12mV2L=2mgL+12mV2H
Step 3: Simplify the Equation
We can cancel m from both sides (assuming m≠0):
12V2L=2gL+12V2H
Multiplying through by 2 to eliminate the fraction:
V2L=4gL+V2H(1)
Step 4: Analyze Forces at the Highest Point
At the highest point, for the string to just go slack, the tension T must be zero. The only forces acting on the mass at the highest point are its weight mg and the centripetal force requirement.
Using Newton's second law, we have:
mg=mV2HL
Cancelling m (again assuming m≠0):
g=V2HL
Rearranging gives us:
V2H=gL(2)
Step 5: Substitute V2H into the Energy Equation
Now we substitute equation (2) into equation (1):
V2L=4gL+gL
V2L=5gL
Step 6: Solve for VL
Taking the square root of both sides:
VL=√5gL
Final Answer
The maximum velocity at the lowest point such that the string just goes slack at the highest point is:
VL=√5gL
---
We have a mass moving in a vertical circle of radius L. At the lowest point, we denote the velocity as VL and at the highest point as VH. The goal is to find VL such that the tension in the string is zero at the highest point.
Using the conservation of mechanical energy, we can equate the total mechanical energy at the lowest point and the highest point.
- Potential Energy (PE) = 0
- Kinetic Energy (KE) = 12mV2L
- Potential Energy (PE) = mg(2L)=2mgL
- Kinetic Energy (KE) = 12mV2H
12mV2L=2mgL+12mV2H
We can cancel m from both sides (assuming m≠0):
12V2L=2gL+12V2H
V2L=4gL+V2H(1)
At the highest point, for the string to just go slack, the tension T must be zero. The only forces acting on the mass at the highest point are its weight mg and the centripetal force requirement.
mg=mV2HL
g=V2HL
V2H=gL(2)
Now we substitute equation (2) into equation (1):
V2L=4gL+gL
V2L=5gL
Taking the square root of both sides:
VL=√5gL
The maximum velocity at the lowest point such that the string just goes slack at the highest point is:
VL=√5gL
Topper's Solved these Questions
Similar Questions
One end of string of length 1.5 m is tied to a stone of mass 0.4 kg and the other end to a small pivot on a smooth vertical board. What is the minimum speed of the stone required at its lowermost.point so that the string does not slack at any point in its motion along the vertical circle ?
View SolutionAssertion For looping a verticla loop of radius, r the minimum velocity at lowest point should be √5gr. Reason In this event the velocityh at the highest point will be zero.
View SolutionA bob is attached to a string of length l whose other end is fixed and is given horizontal velocity at the lowest point of the circle so that the bob moves in a vertical plane. Match the velocity given at the lowest point of circle in column I with tension and velocity at the highest point of the circle corresponding to velocity of column I of column II

View SolutionA ball of mass 100 g is made to loop-the-loop in a vertical circle as shown in Fig. 7.1.29. The radius of the circle is 0.5 m (i)-What is the critical velocity at the highest point of the track ? (ii) If the velocity of the ball at the highest point of the track is twice the critical velocity what is the force exerted by the ball against track?
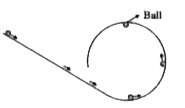
View SolutionA horizontal cylinder is fixed, its inner surface is smooth and its radius is R. A small block is initially at the lowest point. The minimum velocity that should by given to the block at the lowest point, so that it can just cross the point P is u then
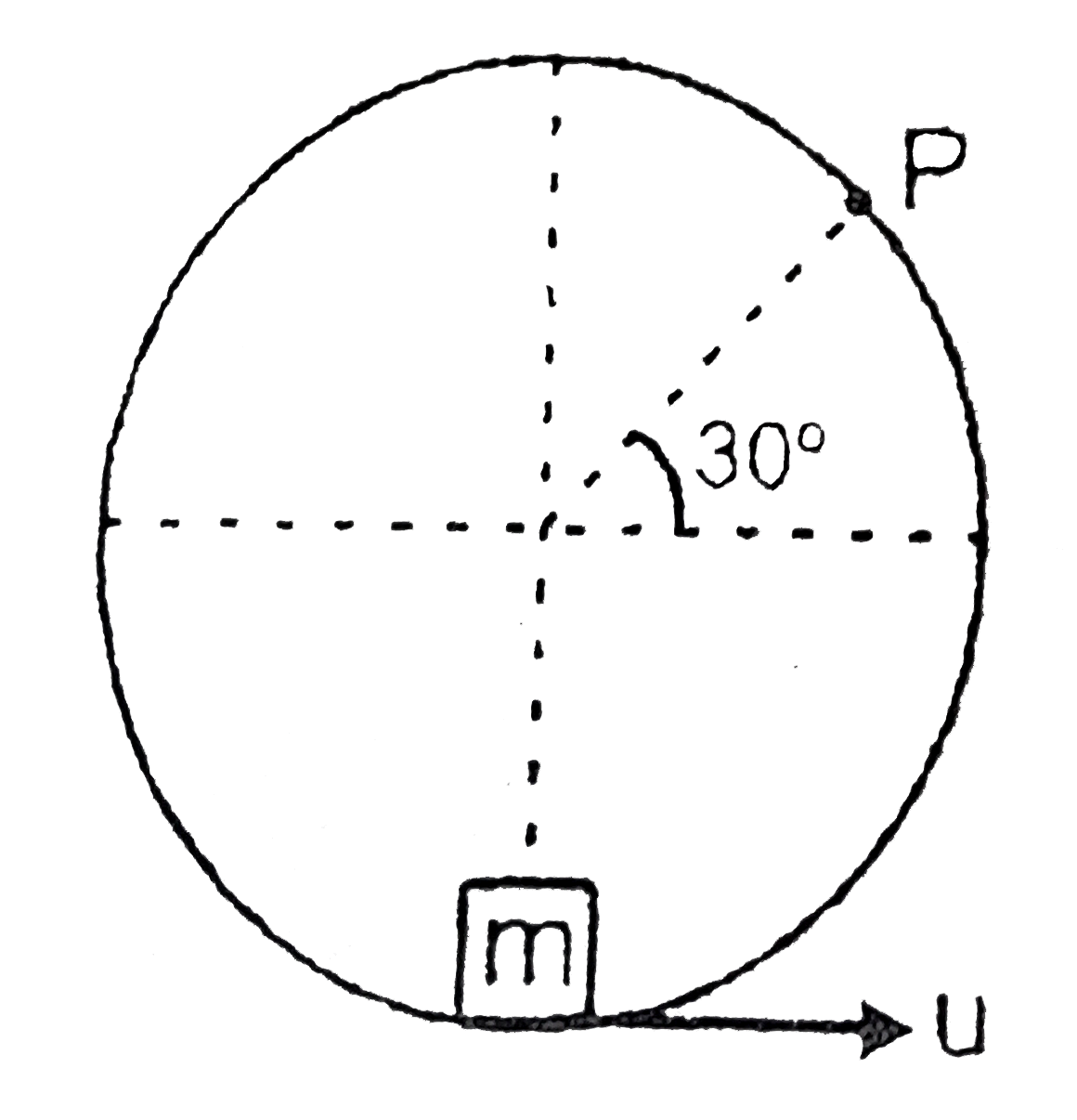
View SolutionA bead is free to slide down on a smooth wire rightly stretched between points AandB on a vertical circle of radius 10m. Find the time taken by the bead to reach point B, if the bead slides from rest from the highest point A on the circle.
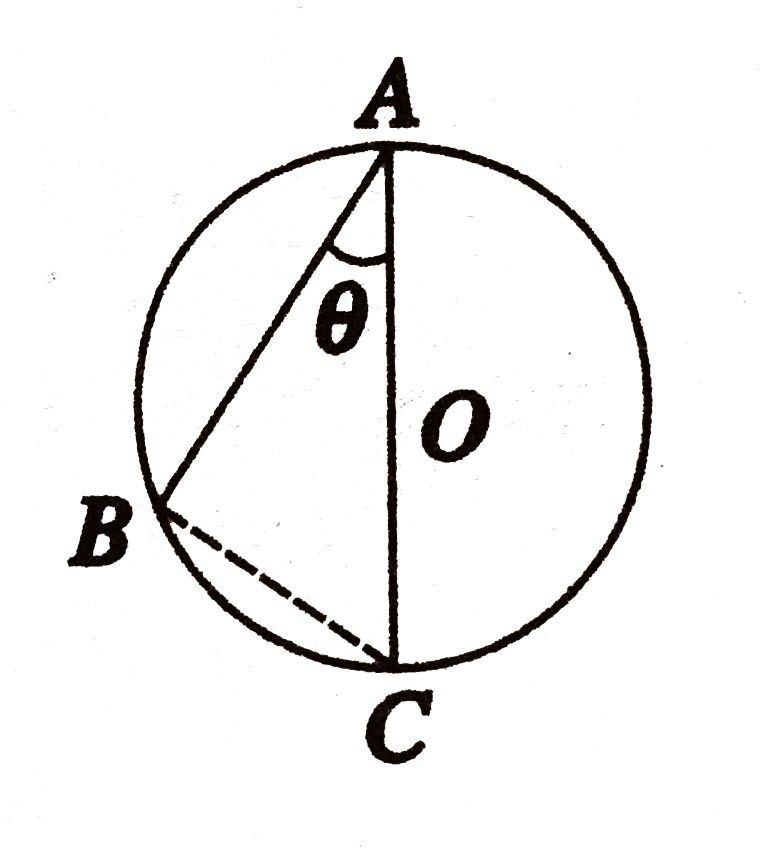 .
.
View SolutionA particle is projected so as to just move along a vertical circle of radius r. The ratio of the tension in the string when the particle is at the lowest and highest point on the circle is infinite
View SolutionThe projectile has only vertical component of velocity at the highest point of its trajectory.
At the highest point, only one component of velocity is present.
View SolutionA small sphere tied to the string of length 0.8m is describing a vertical circle so that the maximum and minimum tensions in the string are in the ratio 3:1. The fixed end of the string is at a height of 5.8m above ground.
(a) Find the velocity of the sphere at the lowest position.
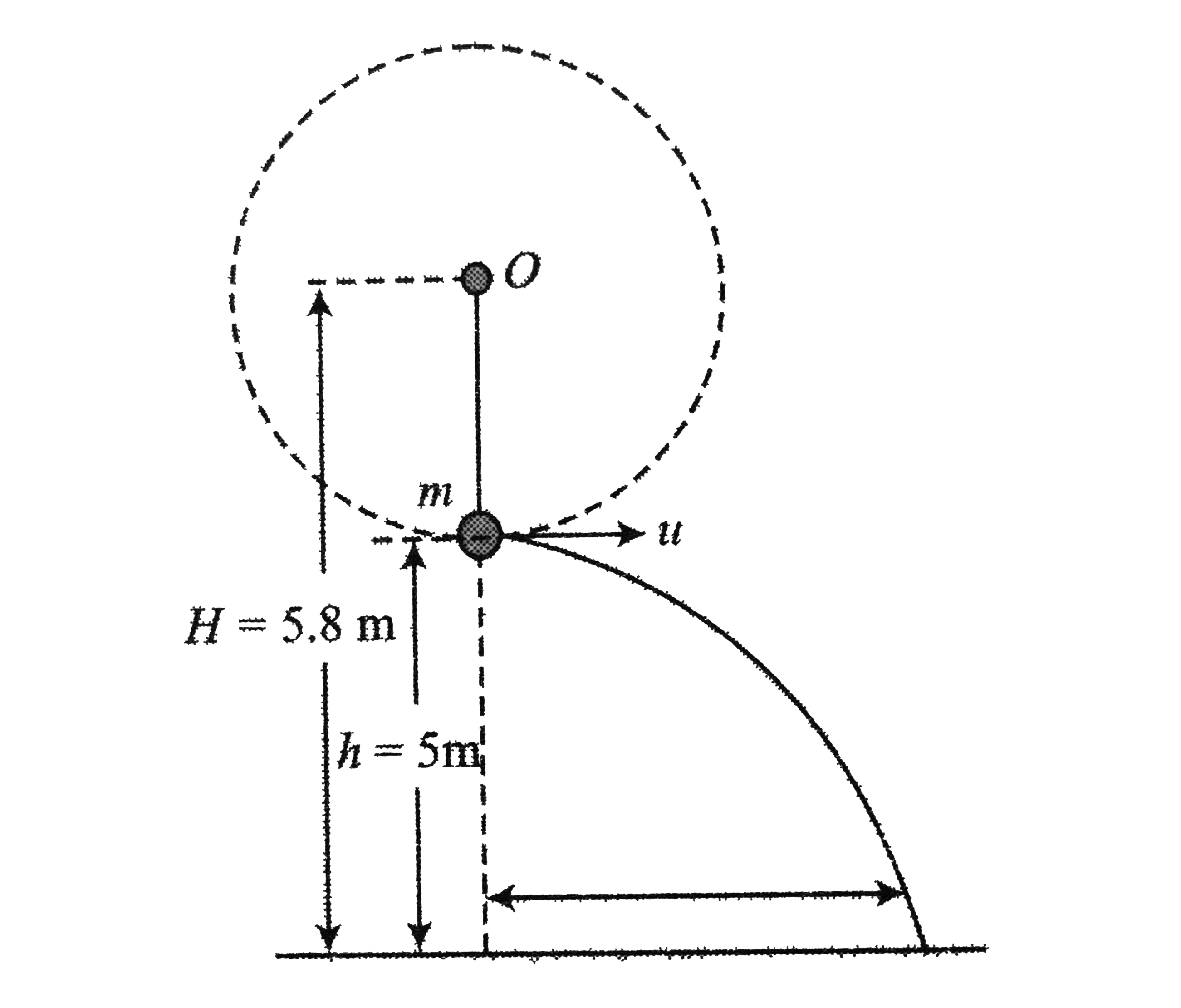
(b) If the string suddenly breaks at the lowest position, when and where will the sphere hit the ground?
View SolutionA particle in projected with velocity √3gL at point A (lowest point of the circle) in the vertical plane. Find the maximum height about horizontal level of point A if the string slacks at the point B as shown in figure.

View Solution
