A mass is supported on a frictionless horizontal surface. It is attached to a string and rotates about a fixed centre with a angular velocity ω0. If the length of the string and angular velocity are doubled, the tension in the string which was initially T0 is now
T0
T0/2
4T0
8T0
The correct Answer is:D
T0=mω2l
T=m(2ω)2×2l=8T0
Topper's Solved these Questions
Similar Questions
A stone is tied to one end of a string and rotated in horizontal circle with a uniform angular velocity. The tension in the string is T, if the length of the string is halved and its angular velocity is doubled , the tension in the string will be
View SolutionAngular momentum of a rigid body rotating about a fixed Axis with angular velocity →ω
View SolutionA particle attached to a string is rotating with a constant angular velocity and its angular momentum is L. If the string is halved and angular velocity is kept constant, the angular momentum will be
View SolutionA ball is whirled in a circle by attaching it to a fixed point with a string. Is there an angular rotation of the ball about its centre? If yes, is this angular velocity equal to the angular velocity of the ball about the fixed point?
View SolutionIn the figure, a ball of mass m is tied with two strings of equal as shown. If the rod is rotated with angular velocity ω1 when
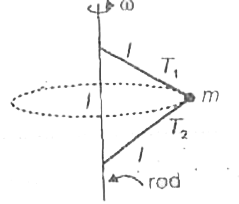 View Solution
View SolutionA stone tied to a string of length l is whirled in a horizontal circle at a constant angular speed ω in a circle of radius r. If the string makes an angle θ with vertical then the tension in the string is :
View SolutionFigure shows a mass m placed on a frictionless horizontal table and attached toa string passing through a mall hole in the surface. Initially, themas movesin a circle of radius r0 with a speed v0 and the ree end of the string is held by a person. The person pulls on the string slowly to decrease the radius of th circle of r. a. Find the tension in the string when the mass moves in the circle of radius r. b. Calculate the chasnge in the kinetic energy of the mass
View SolutionA uniform disc of mass M, radius R is attached to a frictionless horizontal axis. Its rim is wound with a light string and a tension T is applied to it, the angular acceleration will be?
View SolutionA bob in tied to a string of length l & and kept on a horizontal rough surface as shown in the figure when point O of the string is fixed. The bob is given a tangential velocity V0 keeping the string taut as shown in figure. Find the tension in the string as a function of time. The coefficient of kinetic friction is μ.
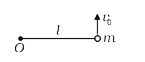 View Solution
View SolutionA ring of radius 'r' and mass per unit length 'm' rotates with an angular velocity 'ω' in free space then tension will be :
View Solution
