Find the electric flux due to a point charge 'Q' through the circular region of radius R if the charge is placed on the axis of ring at a distance x.
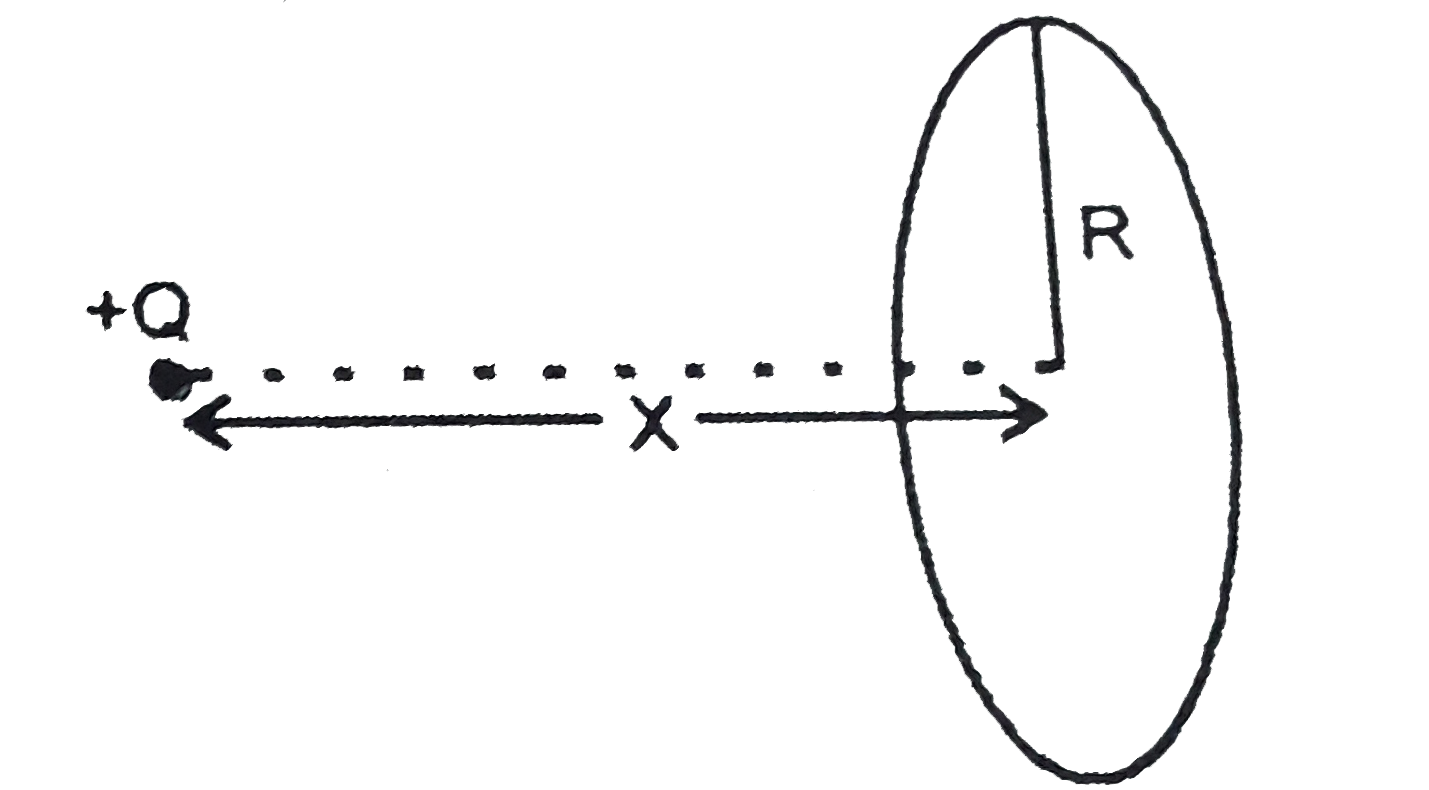
We can divide the circular region into small rings.
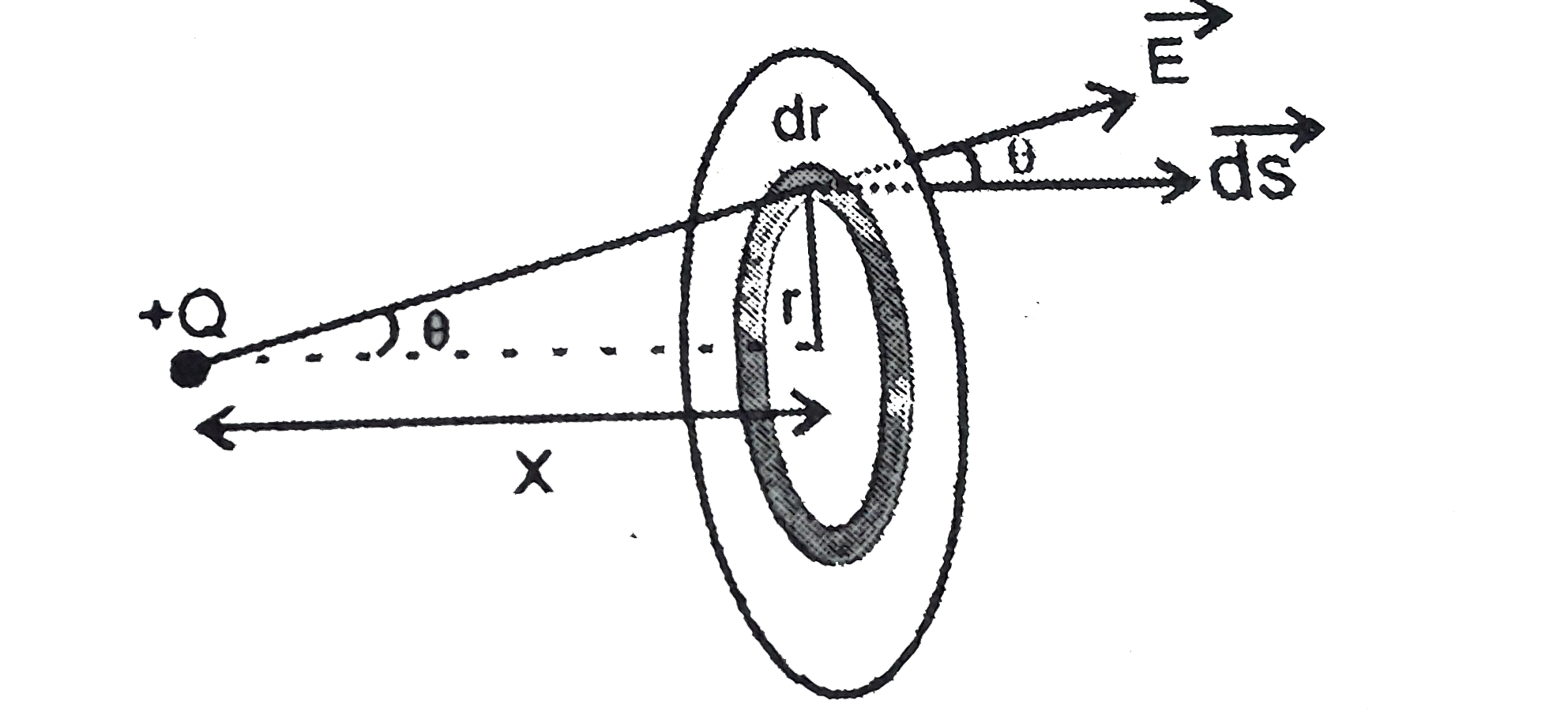
Lets take a ring of radius r and width dr. Flux through this small element dϕ=Edscosθ
∴ϕnet=∫Edscosθ=r−R∫r=0KQ(x2+r2)(2πrdr)(x√x2+r2)=Q2∈0[1−x√x2+R2]
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Problems22videos
ELECTROSTATICS
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise-1 Section (A)9videos
ELECTROSTATICS
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - A.l.P19videos
ELECTROMAGNETIC INDUCTION
- BOOK - RESONANCE ENGLISHCHAPTER - EXPERIMENTAL PHYSICSEXERCISE - PART -II10videos
EXPERIMENTAL PHYSICS
Similar Questions
The flux of electric field through the circular region of radius r as shown in the figure is
_PHY_E05_291_Q01.png)
View SolutionFind the flux of point charge q through the square surface ABCD as shown
View SolutionFind the electric field at the centre of a uniformly charged semicircular ring of radius R. Linear charge density is λ
View SolutionFind the electric field due to an infinitely long cylindrical charge distribution of radius R and having linear charge density λ at a distance half of the radius from its axis.
View SolutionA point charge q is placed at origin. Find the flux of electric,produced due to this charge, through a circle of radius R lying in y-z plane. The centre of the circle lies at (x,0).
View SolutionElectric charge Q is uniformly distributed around a thin ring of radius a. find the potential a point P on the axis of the ring at a distance x from the centre of the ring .
View SolutionA positive charge Q is uniformly distributed along a circular ring of radius R.a small test charge q is placed at the centre of the ring.
View SolutionA positive charge Q is uniformly distributed along a circular ring of radius R.a small test charge q is placed at the centre of the ring .The
View SolutionPositive charge Q is distributed uniformly over a circular ring of radius R. A particle having a mass m and a negative charge q, is placed on its axis at a distance x from the centre. Find the force on the particle. Assuming x is very less than R, find the time period of oscillation of the particle if it is released from there.
View SolutionA point charge .Q. is placed at a point inside the cone as shown. The flux due to the charge through the curved surface is given as 2Q3ε0. Now another charge .Q. is placed vertically above at the same distance from the base. The flux through the curved surface due to both charges is .
View Solution