A point charge q is placed at origin. Find the flux of electric,produced due to this charge, through a circle of radius R lying in y-z plane. The centre of the circle lies at (x,0).
To find the electric flux through a circle of radius R lying in the y-z plane due to a point charge q placed at the origin, we can follow these steps:
Step 1: Understand the Setup
We have a point charge q located at the origin (0, 0, 0). The circle of radius R lies in the y-z plane, and its center is at the point (x, 0, 0).
Step 2: Electric Field Due to the Point Charge
The electric field E at a distance r from a point charge q is given by the formula:
E=kqr2
where k=14πϵ0 is Coulomb's constant.
Step 3: Determine the Distance from the Charge to the Circle
The distance from the point charge at the origin to any point on the circle can be expressed as:
r=√x2+y2+z2
However, since the circle lies in the y-z plane, we can consider a point on the circle at coordinates (x, y, z) where y2+z2=R2. Thus, the distance from the charge to the center of the circle is:
r=√x2+R2
Step 4: Calculate the Electric Field at the Center of the Circle
Substituting the distance into the electric field formula, we get:
E=kq(x2+R2)
Step 5: Determine the Area Vector of the Circle
The area vector A of the circle is perpendicular to the surface of the circle and points along the x-axis. The magnitude of the area A of the circle is given by:
A=πR2
Step 6: Calculate the Electric Flux
The electric flux ΦE through the circle is given by the dot product of the electric field E and the area vector A:
ΦE=E⋅A=E⋅A⋅cos(0∘)
Since the electric field and area vector are in the same direction (along the x-axis), cos(0∘)=1:
ΦE=E⋅A
Substituting the values we have:
ΦE=(kq(x2+R2))⋅(πR2)
ΦE=kqπR2(x2+R2)
Step 7: Substitute the Value of k
Substituting k=14πϵ0:
ΦE=14πϵ0qπR2(x2+R2)
ΦE=qR24ϵ0(x2+R2)
Final Result
Thus, the electric flux through the circle of radius R in the y-z plane due to the point charge q at the origin is:
ΦE=qR24ϵ0(x2+R2)
---
We have a point charge q located at the origin (0, 0, 0). The circle of radius R lies in the y-z plane, and its center is at the point (x, 0, 0).
The electric field E at a distance r from a point charge q is given by the formula:
E=kqr2
where k=14πϵ0 is Coulomb's constant.
The distance from the point charge at the origin to any point on the circle can be expressed as:
r=√x2+y2+z2
However, since the circle lies in the y-z plane, we can consider a point on the circle at coordinates (x, y, z) where y2+z2=R2. Thus, the distance from the charge to the center of the circle is:
r=√x2+R2
Substituting the distance into the electric field formula, we get:
E=kq(x2+R2)
The area vector A of the circle is perpendicular to the surface of the circle and points along the x-axis. The magnitude of the area A of the circle is given by:
A=πR2
The electric flux ΦE through the circle is given by the dot product of the electric field E and the area vector A:
ΦE=E⋅A=E⋅A⋅cos(0∘)
Since the electric field and area vector are in the same direction (along the x-axis), cos(0∘)=1:
ΦE=E⋅A
Substituting the values we have:
ΦE=(kq(x2+R2))⋅(πR2)
ΦE=kqπR2(x2+R2)
Substituting k=14πϵ0:
ΦE=14πϵ0qπR2(x2+R2)
ΦE=qR24ϵ0(x2+R2)
Thus, the electric flux through the circle of radius R in the y-z plane due to the point charge q at the origin is:
ΦE=qR24ϵ0(x2+R2)
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - TRY YOURSELF
33 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - ASSIGNMENT(SECTION-A) Objective Type Question
45 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - ASSIGNMENT(SECTION -D) Assertion-Reason type Question)
15 Videos
Similar Questions
A point charge q is placed at the origin . How does the electric field due to the charge very with distance r from the origin ?
View SolutionA point charge Q is placed at the origin . Find the electrostatic energy stored outside the sphere of radius R centred at the origin.
View SolutionFind the electric flux due to a point charge 'Q' through the circular region of radius R if the charge is placed on the axis of ring at a distance x.
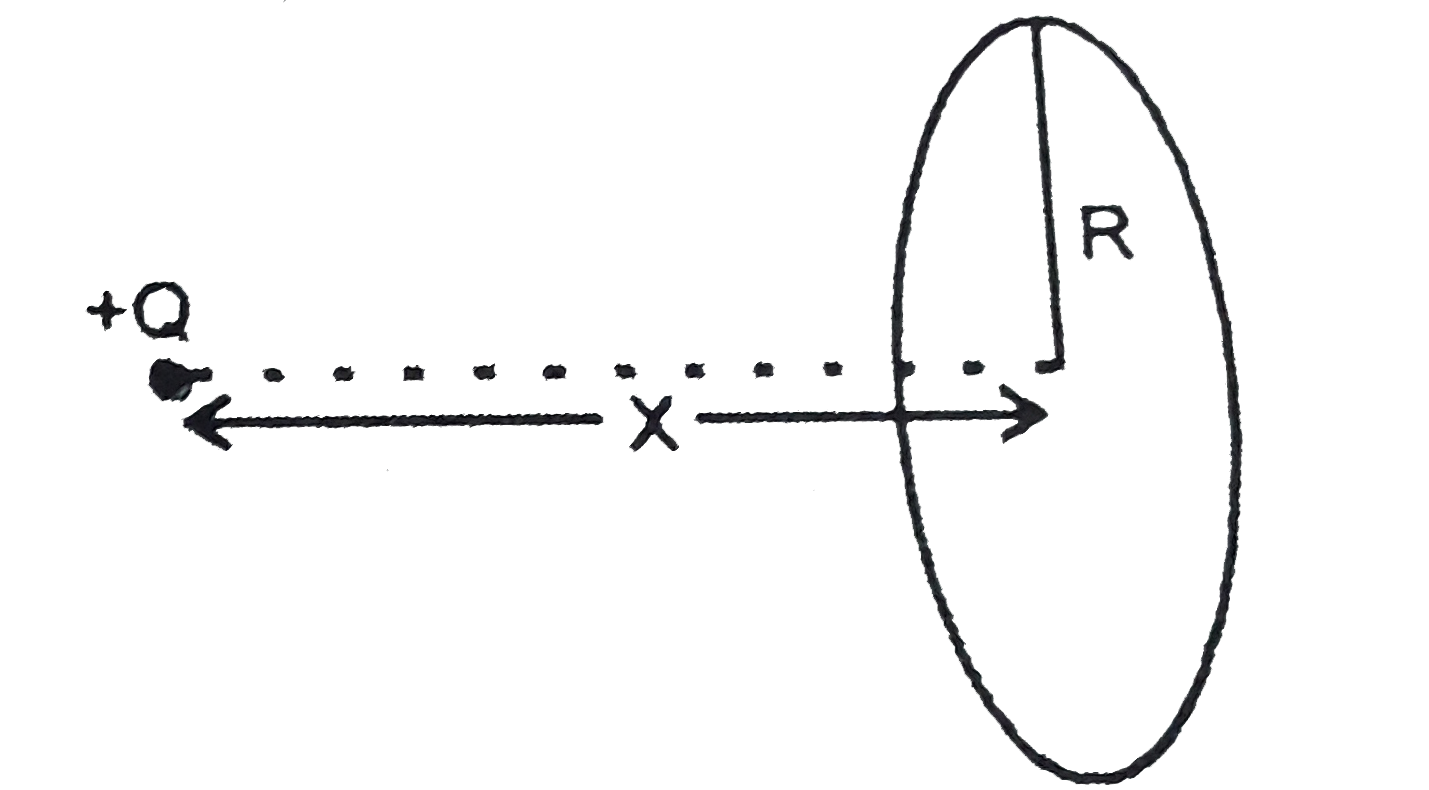
View SolutionA charge Q is placed at the centre of a cube. Find the flux of the electric field through the six surfaced of the cube.
View SolutionA charge q is placed at point D of the cube. Find the electric flux passing through the EFGH and face AEHD.
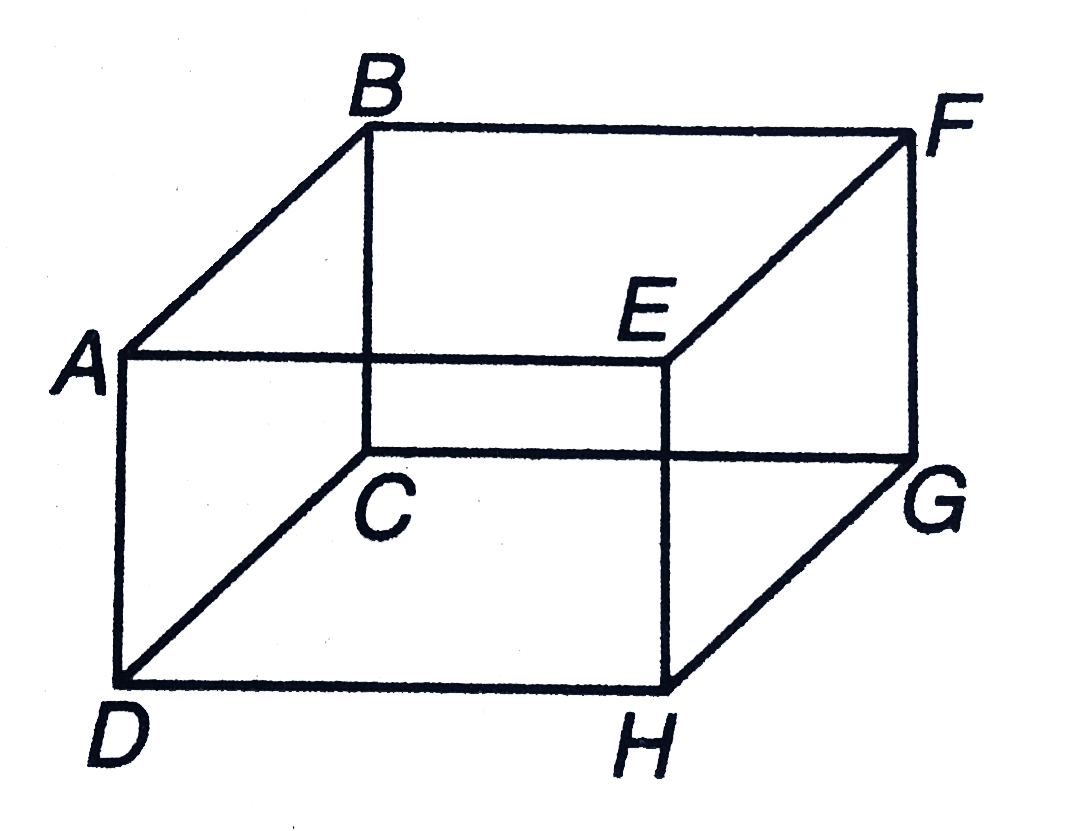
View SolutionA point charge .Q. is placed at a point inside the cone as shown. The flux due to the charge through the curved surface is given as 2Q3ε0. Now another charge .Q. is placed vertically above at the same distance from the base. The flux through the curved surface due to both charges is .

View SolutionA point charge +q is placed at the centre of curvature of a hemisphere. Find flux through the hemispherical surface.
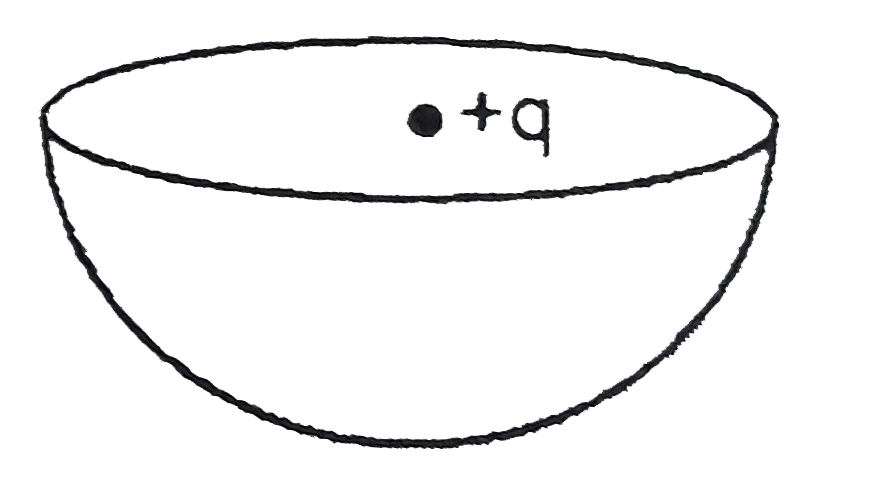
View SolutionTwo point charges q and -q are separated by a distance 2a. Evaluate the flux of the electric field strength vector across a circle of radius R.

View SolutionTwo charges of magnitudes +4Q and -Q and located at points (a, 0) and (-3a, 0) respectively. What is the electric flux due to these charges through a sphere of radius '2a' with its centre at the orgin ?
View SolutionA charge +Q is placed on middle of edge of the cube.Then electric flux through cube due to field of charge +Q is
View Solution
