Find the electric field due to an infinitely long cylindrical charge distribution of radius R and having linear charge density λ at a distance half of the radius from its axis.
r=R2 point will be inside so E=2kλrR2=2kλR2(R2)=λ4π∈0R
Topper's Solved these Questions
- MISCELLANEOUSBook:ALLENChapter:MISCELLANEOUSExercise:Part -II Example Some worked out Examples
Explore 1 Video
- MISCELLANEOUSBook:ALLENChapter:MISCELLANEOUSExercise:Exercise-01
Explore 87 Videos
- MISCELLANEOUSBook:ALLENChapter:MISCELLANEOUSExercise:Question
Explore 1 Video
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Book:ALLENChapter:KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Exercise:BEGINNER S BOX-7
Explore 8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT Book:ALLENChapter:PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT Exercise:EXERCISE-IV
Explore 8 Videos
Similar Questions
Knowledge Check
An infinite cylinder of radius ro, carrying linear charge density λ. The equation of the equipotential surface for the cylinder is
Ar=r0eπε0[V(r)+V(r0)]λBr=r0e2πε0[V(r)−V(r0)]λ2Cr=r0e−2πε0[V(r)=V(r0)]λDr=r0e−2πε0[V(r)−V(r0)]λ
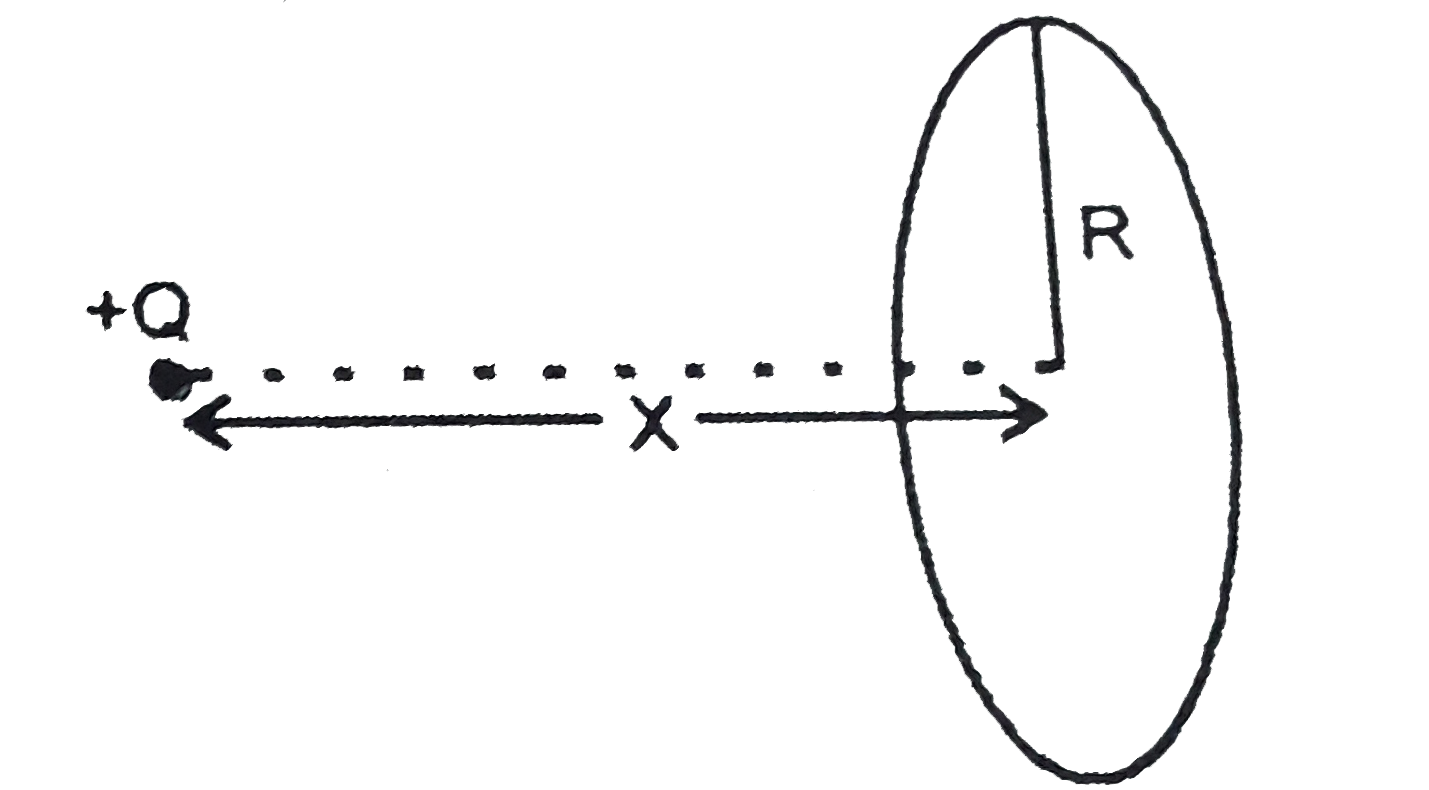
Find the electric flux due to a point charge 'Q' through the circular region of radius R if the charge is placed on the axis of ring at a distance x.
View SolutionElectric field at centre O of semicircule of radius 'a' having linear charge density λ given is given by

View SolutionA charged disc of radius 3 m has charge density σ. Electric field at a distance of 4 m from its centre on axis is _______
View SolutionElectric field at a point of distance r from a uniformly charged wire of infinite length having linear charge density λ is directly proportional to
View SolutionIntensity of electric field at a point at a perpendicular distance .r. from an infinite line charge, having linear charge density .λ. is given by :
View SolutionFind electric field at point A, B, C, D due to infinitely long uniformly charged wire with linear charge density λ and kept along z-axis (as shown in figure). Assume that all the parameters are in S.l. units.

View SolutionIntensity of electric field at a point at a perpendicular distance .r. from an infinite line charge, having linear charge density .λ. is given by :
View Solution

