A charged disc of radius 3 m has charge density σ. Electric field at a distance of 4 m from its centre on axis is _______
3σ5ε0
σ10ε0
σ8ε0
None
The correct Answer is:B
To find the electric field at a distance of 4 m from the center of a charged disc with a radius of 3 m and charge density σ, we can use the formula for the electric field along the axis of a uniformly charged disc. The formula is given by:
E=σ2ϵ0(1−x√r2+x2)
where:
- E is the electric field,
- σ is the surface charge density,
- ϵ0 is the permittivity of free space,
- r is the radius of the disc,
- x is the distance from the center of the disc along the axis.
Step 1: Identify the given values
- Radius of the disc, r=3m
- Distance from the center, x=4m
Step 2: Substitute the values into the formula
We substitute r and x into the electric field formula:
E=σ2ϵ0(1−4√32+42)
Step 3: Calculate r2+x2
Calculate r2+x2:
r2+x2=32+42=9+16=25
Step 4: Find the square root
Now, find the square root of 25:
√25=5
Step 5: Substitute back into the electric field formula
Now substitute back into the formula:
E=σ2ϵ0(1−45)
Step 6: Simplify the expression
Now simplify the expression inside the parentheses:
1−45=15
So, we have:
E=σ2ϵ0⋅15
Step 7: Final simplification
This can be simplified to:
E=σ10ϵ0
Conclusion
Thus, the electric field at a distance of 4 m from the center of the charged disc is:
E=σ10ϵ0
The correct answer is σ10ϵ0.
---
- E is the electric field,
- σ is the surface charge density,
- ϵ0 is the permittivity of free space,
- r is the radius of the disc,
- x is the distance from the center of the disc along the axis.
- Radius of the disc, r=3m
- Distance from the center, x=4m
We substitute r and x into the electric field formula:
Calculate r2+x2:
Now, find the square root of 25:
Now substitute back into the formula:
Now simplify the expression inside the parentheses:
This can be simplified to:
Thus, the electric field at a distance of 4 m from the center of the charged disc is:
Topper's Solved these Questions
- ELECTROSTATICSBook:AAKASH SERIESChapter:ELECTROSTATICSExercise:PRACTICE SHEET (EXERCISE - II INTENSITY OF ELECTRIC FIELD) (LEVEL - II (MAIN) STRAIGHT OBJECTIVE TYPE QUESTION)
Explore 10 Videos
- ELECTROSTATICSBook:AAKASH SERIESChapter:ELECTROSTATICSExercise:PRACTICE SHEET (EXERCISE - II INTENSITY OF ELECTRIC FIELD) (LEVEL - II (MAIN) MORE THAN ONE ANSWER TYPE QUESTION)
Explore 1 Video
- ELECTROSTATICSBook:AAKASH SERIESChapter:ELECTROSTATICSExercise:PRACTICE SHEET (EXERCISE - I COULOMB.S INVERSE SQUARE LAQW) (LEVEL - II (ADVANCED LINKED COMPREHENSION TYPE QUESTION)
Explore 3 Videos
- ELECTROMAGNETICSBook:AAKASH SERIESChapter:ELECTROMAGNETICSExercise:ADDITIONAL EXERCISE
Explore 13 Videos
- ELEMENTS OF VECTORSBook:AAKASH SERIESChapter:ELEMENTS OF VECTORSExercise:QUESTIONS FOR DESCRIPTIVE ANSWERS
Explore 10 Videos
Similar Questions
Knowledge Check
Consider a thin spherical shell of radius R consisting of uniform surface charge density σ. The electric field at a point of distance x from its centre and outside the shell is
Ainversely proportional to σBdirectly proportional to x2Cdirectlr proportional to RDinversely proportional to x2
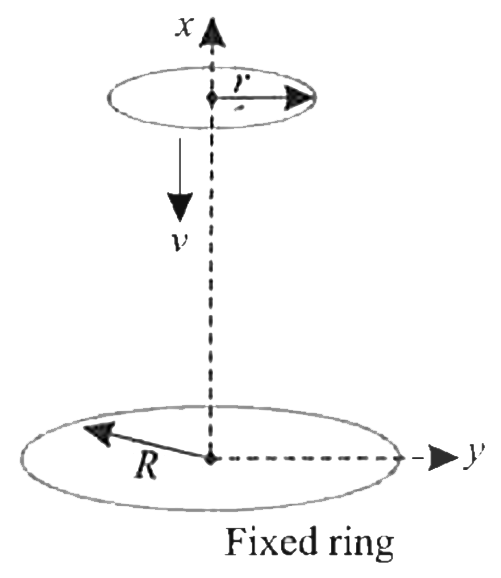
A ring of radius R is placed in the plane its centre at origin and its axis along the x-asis and having uniformly distributed positive charge. A ring of radius r(<<R) and coaxial with the larger ring is moving along the axis with constant velcity , then the variation of electrical flux (ϕ) passing through the smaller ring with position will be best represent by :
View SolutionThe electric field at a distance 3R/2 from the centre of a charge conducting spherical shell of radius R is E. The electric field at a distance R/2 from the centre of the sphere is
View SolutionThe electric field at a distance 3R/2 from the centre of a charge conducting spherical shell of radius R is E. The electric field at a distance R/2 from the centre of the sphere is
View SolutionA hollow spherical conductor of radius 1m has a charge of 250μC then electric intensity at a point distance of 0.5m from the centre of the spherical conductor is
View SolutionAn annular disc of inner radius a and outer radius '2a' is uniformly charged with uniform surface charge density σ. Find the potential at a distance 'a' from the centre at a point 'P' lying on the axis.
View SolutionFind the electric field due to an infinitely long cylindrical charge distribution of radius R and having linear charge density λ at a distance half of the radius from its axis.
View SolutionThe electric field intensity at a distance 20cm from the centre of a uniformly charged non conducting solid sphere of radius 10cm is E.Then what is the electric field intensity at a distance 5cm from the centre it will be.....
View Solution

