Two hemispheres of radii R and r(<R) are fixed on a horizontal table touching each other (see figure). A uniform rod rests on to spheres as shown. The coefficient of friction between the rod and two spherers is μ. Then the maximum value of the ratio rR for which the rod will not slide is :

a.√1+μ2−μ√1+μ2+μ
b.√1+2μ2−μ√1+μ2+μ
c.√2+μ2−μ√1+μ2+μ
d.None of these
The correct Answer is:A

In figure (b)
sinθ=R−rR+r=1−η1+η[whereη=rR]………(1)
The equilibrium of rod gives
N1+N2=Mgcosθ…..(2)
and μ(N1+N2)=mgsinθ .......(3)
Assuming the friction to be at its limiting value.
(3)/(2) gives
tanθ=μ
∴sinθ=μ√1+μ2
Put in (1)
1−μ1+μ=μ√1+μ2
√1+μ2−η√1+μ2=μ+μη
∴√1+μ2−μ√1+μ2+−μ=η
If the ratio η is decreased, θ wil increase and the rod will begin to slide.

Topper's Solved these Questions
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PART - II PHYSICS
106 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems
13 Videos
- TEST SERIESBOOK - RESONANCE ENGLISHCHAPTER - TEST SERIESEXERCISE - PHYSICS
130 Videos
Similar Questions
A particle is placed at rest inside a hollow hemisphere of radius R. The coefficient of friction between the particle and the hemisphere is μ=1√3. The maximum height up to which the particle can remain stationary is
View SolutionA ladder of length 5m is placed against a smooth wall as shown in figure. The coefficient or friction is μ between ladder and ground. What is the minimum value of μ , If the ladder is not to slip?

View Solution
Knowledge Check
Two spheres of equal masses but radii R and 2 R are allowed to fall in a liquid, the ratio of their terminal velocities is
A1:4B1:2C1:32D2:1
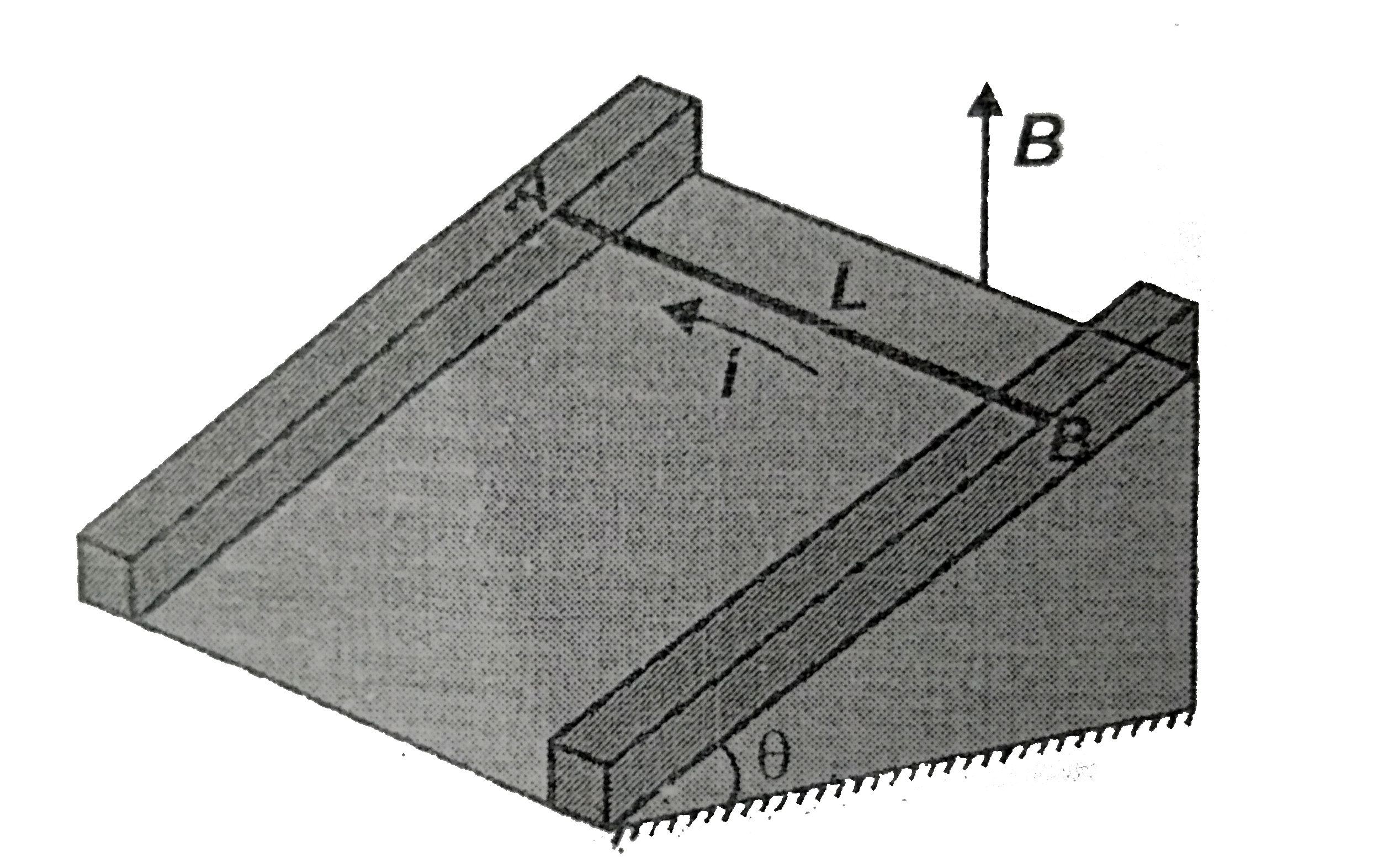
On an inclined plane, two conducting rails are fixed along the line of greatest slope. A conducting rod AB is placed on the radils so that it is horizontal. A vertically upward uniform magnetic field is present in the region. A current i flows through AB from B to A. The mass of AB is m and the coefficient of friction between the rod and rails is μ. Find the minimum and maximum value of B, so that the rod can stay in equilibrium. Assume that μ<tanθ
View SolutionIn the figure shown, a solid sphere of mass 'm' and radius r is released from a height 6r to slide down a smooth surface. A plank of same mass 'm' touches the horizontal portion of the surface at the ground. The co-efficient of friction between the plank and the sphere is μ and that between the plank and the ground is μ/4. Find the work done by the friction force between the plank and the ground till the sphere starts pure rolling on the plank. Neglect the height of the plank.

View SolutionA copper rod of mass m rests on two horizontal rails distance L apart and carries a current of I from one rail to the other. The coefficient of static friction between rod and rails is μs What are the (a) magnitude and (b) angle (relative to the vertical) of the smallest magnetic field that puts the rod on the verge of sliding?
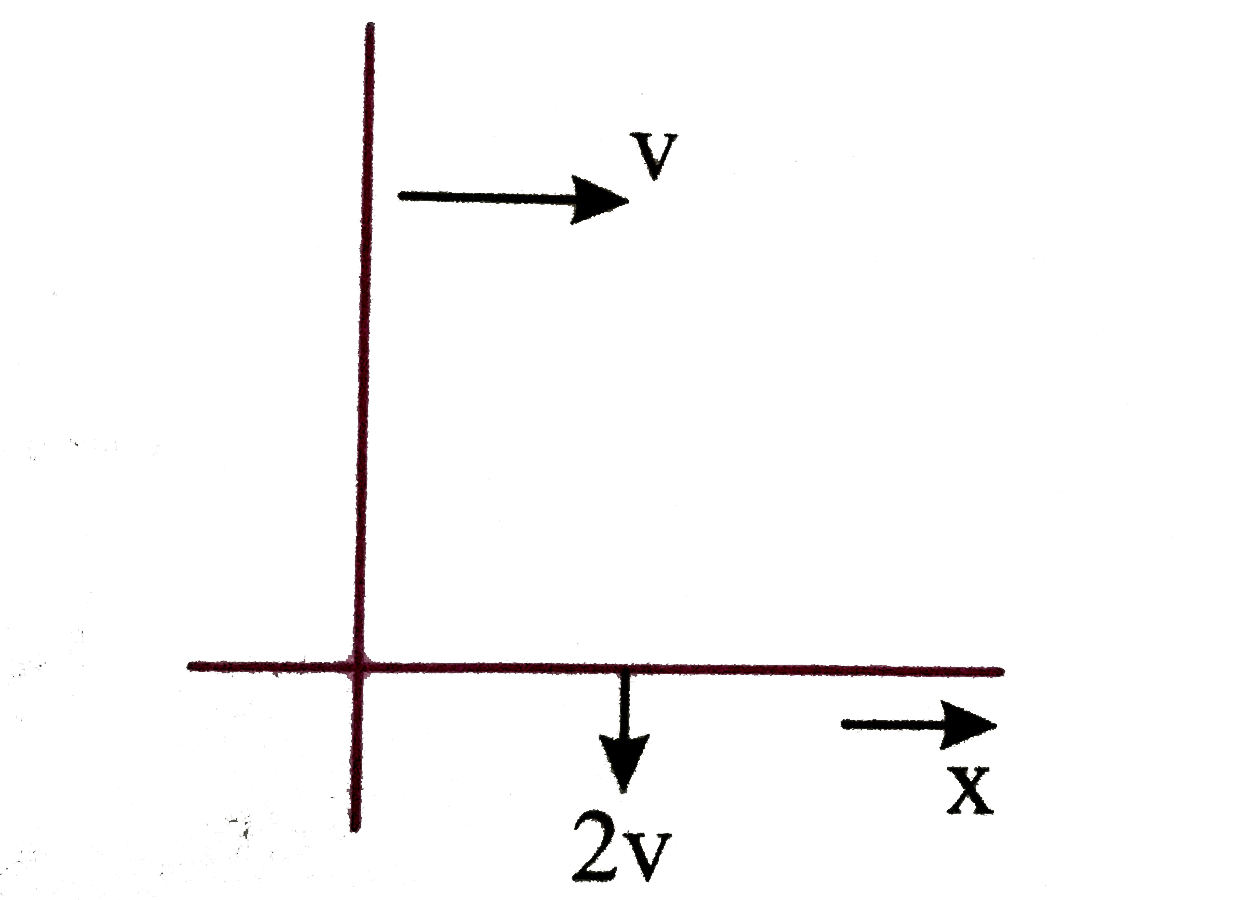
View SolutionTwo thin roads are moving perpendicularly as shown in the figure. If the friction acting between them is FR then the unit vector in the direction of friction force acting on the rod lying along x-axis is
View SolutionThree plates A, B and C are placed close to each other with +Q charge given to the middle plate. The inner surfaces to A and C can be connected to earth through plate D and keys K1 and K2 . The plates D is a dielectric slab with dielectric constant K1 then the charge that will flow through plate D and keys K1 and K2 . The plate D is a dielectric slab with dielectric constant K, then the charge that will flow though plate D when K2 is closed and K2 is open is

View SolutionTwo soap bubbles of radii r1 and r2 equal to 4 cm and 5 cm are touching each other over a common surface S1S2 (shown in figure). Its radius will be
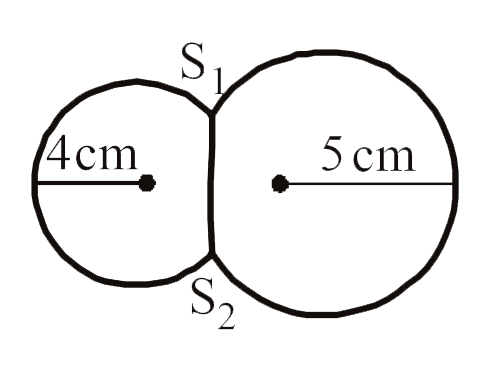
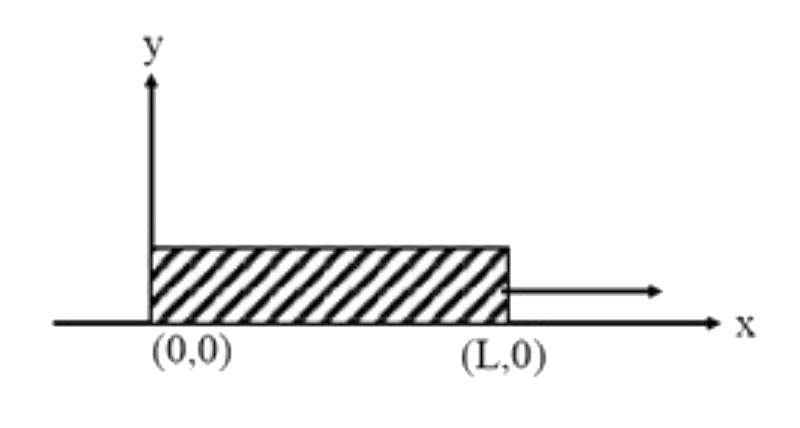
View SolutionA uniform rod of length L and mass M has been placed on a rough horizontal surface as shown in the figure. The rod is pulled by applying a horizontal force. The coefficient of friction μ between the surface and the rod is given by
μ={μ0x0≤x≤L0x>L, where μ0 is a positive constant. The heat generated due to friction as the rod moves by a distance L is
View Solution
