Figure shows a circular frications trck of radius R, centred at point O. A particle of mass M is released from point A(OA=R/2). After collision with the track, the particle moves along on the track. Then the coefficient of restitution e is.

0.2
0.5
1
zero
The correct Answer is:D
cosθ=12⇒θ=π3
(a) After collision the particle moves along the track. This means there is no normal component of velocity, Hence e=0
(b) Just before collision, the compoenents of velocity along the normal and along the tangent are
un=usinθ
ut=ucosθ

During collision ut does not change. The normal component of velocity becomes eun along →BO.
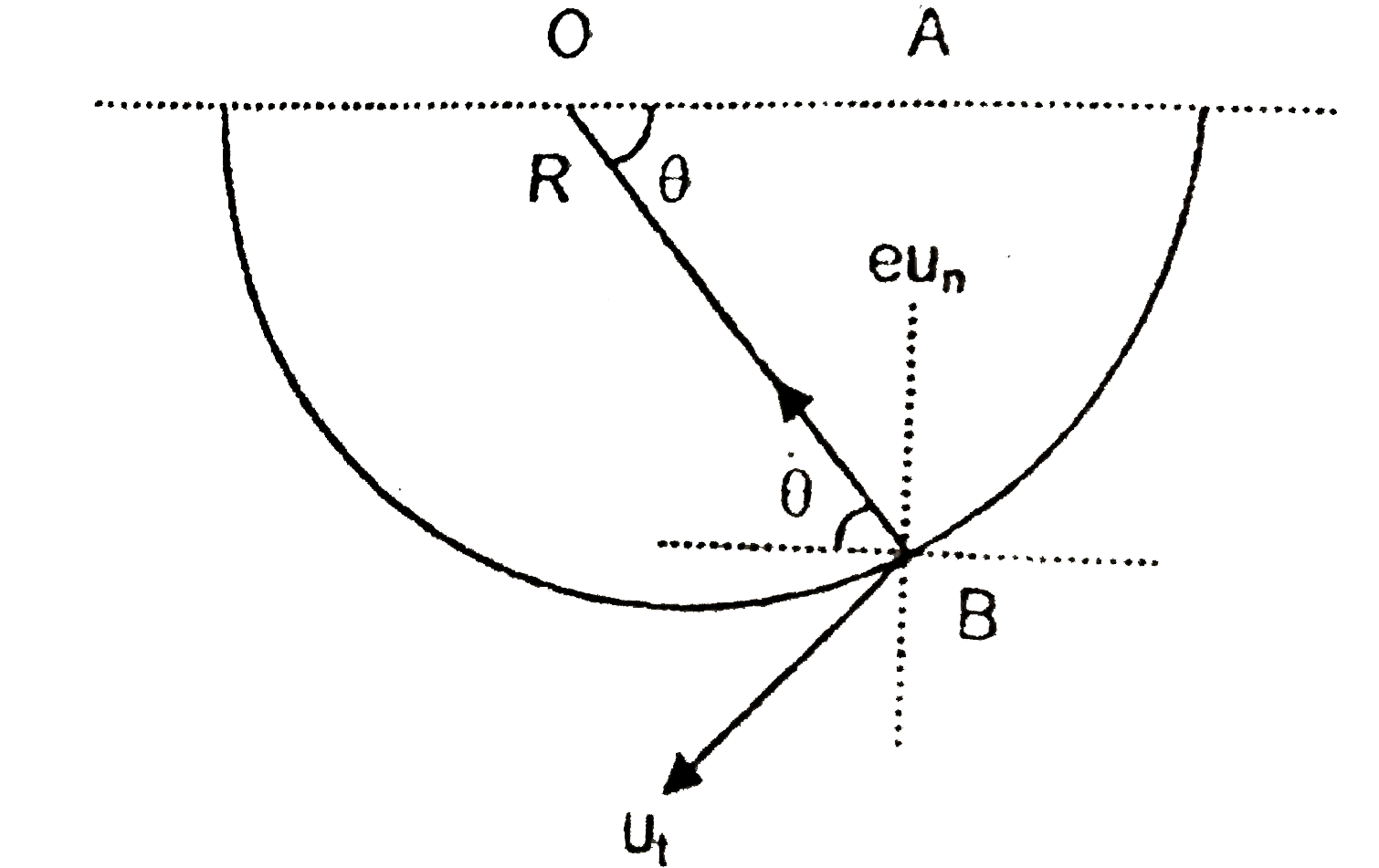
Question says that velocity of the particle is horizontal after collision, which mean sutcosθ=eunsinθ
ucos2θ=eusin2θ⇒e=cot2'π3=13
Topper's Solved these Questions
- TEST PAPERSBook:RESONANCE ENGLISHChapter:TEST PAPERSExercise:PART - II PHYSICS
Explore 106 Videos
- SIMPLE HARMONIC MOTION Book:RESONANCE ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:Advanced Level Problems
Explore 13 Videos
- TEST SERIESBook:RESONANCE ENGLISHChapter:TEST SERIESExercise:PHYSICS
Explore 130 Videos
Similar Questions
A particle of mass m collides with another stationary particle of mass M such that the second particle starts moving and the first particle stops just after the collision. Then which of the following conditions must always be valid ?
View SolutionA particle of mass m is released from point A as shown in the gigure. Would it loop the loop if H=4r? What is the force on the circular track when it is at point (a) B, (b) C?

View Solution
Knowledge Check
A particle is moving on a circular path of radius R with constant speed v. During motion of the particle form point A to point B
 AAverage speed is v/2BThe magnitude of average velocity is v/πCThe magnitude of average acceleration is 2v2πRDAverage velocity is zero.
AAverage speed is v/2BThe magnitude of average velocity is v/πCThe magnitude of average acceleration is 2v2πRDAverage velocity is zero.
A block of mass M with a semi - circular track of radius R rests on a smooth floor. A sphere of mass m and radius r is released from rest from A. Find the velocity of sphere and track , when the sphere reaches B.

View SolutionA wedge of mass M is kept at rest on smooth surface a particle of mass m hits the wedge normally. Find the velocity of wedge and particle just after collision. Take coefficient of restitution as e.
View Solution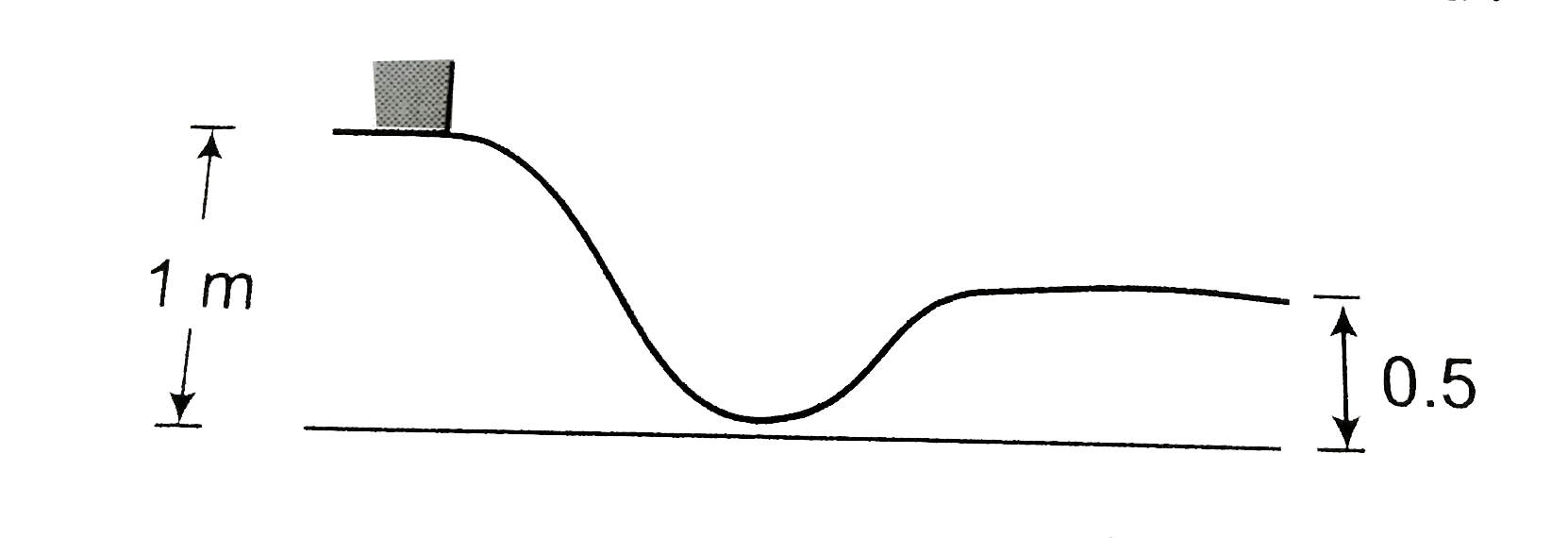
The figure shown a particle sliding on a frictionless track, which teminates in a straight horizontal section. If the particle starts slipping from the point A, how far away from the track will the particle hit the ground?
View Solution
The figure shown a particle sliding on a frictionless track, which teminates in a straight horizontal section. If the particle starts slipping from the point A, how far away from the track will the particle hit the ground?
View SolutionCentripetal acceleration of a particle of mass m moving in a circle of radius r is 4/r2. What is the angular momentum of the particle ?
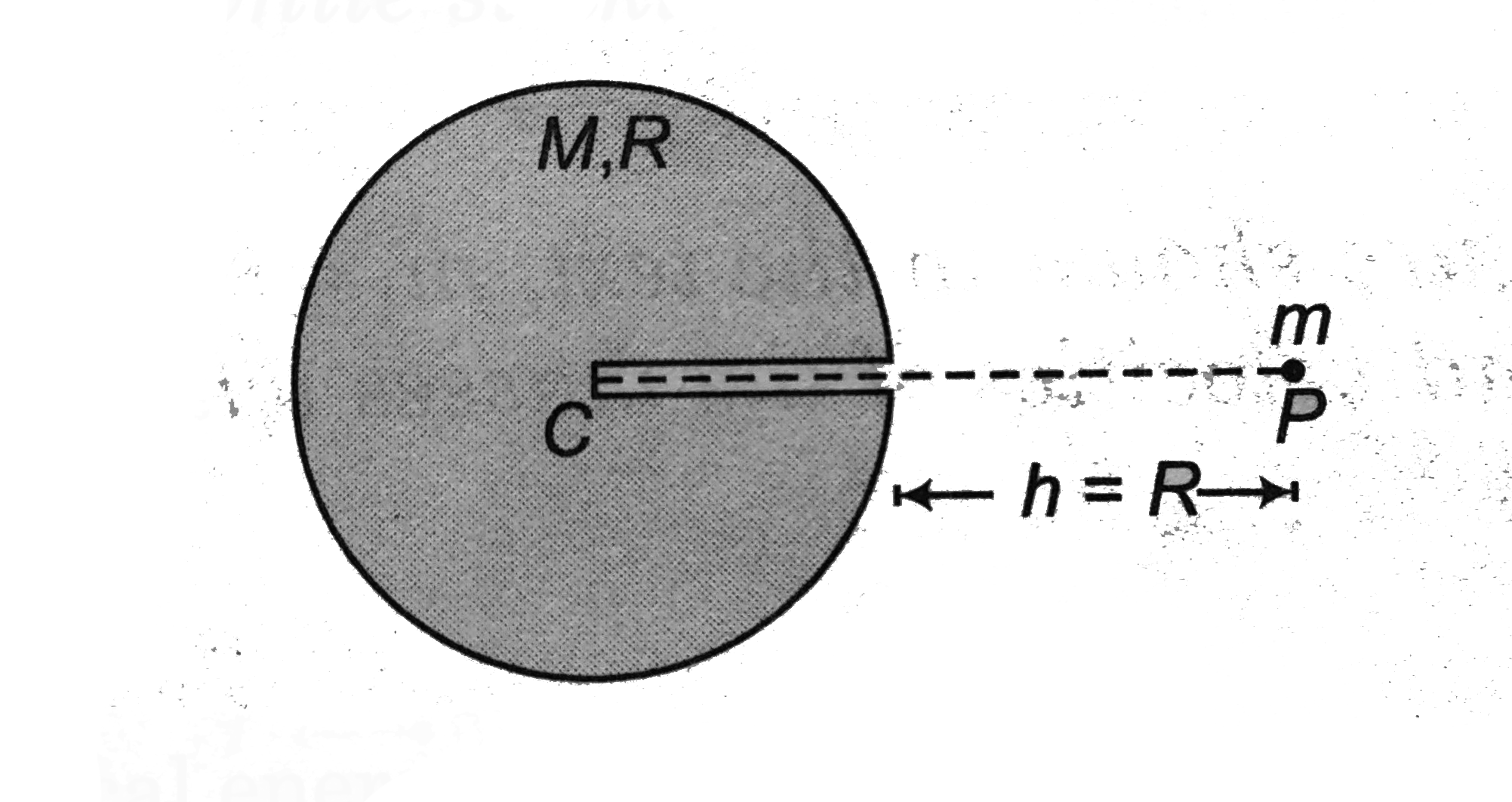
View SolutionThere is a smooth tunnel upto centre C of a solid sphere of mass 'M' and radius R.A particle of mass m(<<M) is released from point P along the line CP. Find velocity of 'm' while striking at C.
 .
.
View SolutionPositive charge Q is distributed uniformly over a circular ring of radius R. A particle having a mass m and a negative charge q, is placed on its axis at a distance x from the centre. Find the force on the particle. Assuming x is very less than R, find the time period of oscillation of the particle if it is released from there.
View Solution

