A liquid is flowing through a horizontal channel. The speed of flow depends on height from the floor as . Where is the height of liquid in the channel and is the speed of the top layer. Coefficient of viscosity is . Then the shear stress that the liquid exerts on the floor is.
The correct Answer is:A
To find the shear stress that the liquid exerts on the floor of a horizontal channel, we can follow these steps:
1. Understand the Velocity Profile:
The speed of flow v is given by the equation:
v=v0(2yh−(yh)2)
where v0 is the speed of the top layer, h is the height of the liquid in the channel, and y is the height from the floor.
2. Calculate the Velocity Gradient:
The velocity gradient (which is the change in velocity with respect to height) is given by:
dvdy
To find this, we differentiate v with respect to y:
dvdy=ddy(v0(2yh−(yh)2))
Using the product and chain rules, we get:
dvdy=v0(2h−2yh2)
3. Evaluate the Velocity Gradient at the Floor:
At the floor, where y=0:
dvdy∣∣∣y=0=v0(2h−0)=2v0h
4. Use the Shear Stress Formula:
The shear stress τ exerted by the liquid on the floor can be calculated using the formula:
τ=ηdvdy
Substituting the value of the velocity gradient we found:
τ=η(2v0h)
5. Final Expression for Shear Stress:
Thus, the shear stress that the liquid exerts on the floor is:
τ=2ηv0h
Conclusion:
The shear stress exerted by the liquid on the floor of the channel is given by:
τ=2ηv0h
The speed of flow v is given by the equation:
v=v0(2yh−(yh)2)
where v0 is the speed of the top layer, h is the height of the liquid in the channel, and y is the height from the floor.
The velocity gradient (which is the change in velocity with respect to height) is given by:
dvdy
To find this, we differentiate v with respect to y:
dvdy=ddy(v0(2yh−(yh)2))
Using the product and chain rules, we get:
dvdy=v0(2h−2yh2)
At the floor, where y=0:
dvdy∣∣∣y=0=v0(2h−0)=2v0h
The shear stress τ exerted by the liquid on the floor can be calculated using the formula:
τ=ηdvdy
Substituting the value of the velocity gradient we found:
τ=η(2v0h)
Thus, the shear stress that the liquid exerts on the floor is:
τ=2ηv0h
The shear stress exerted by the liquid on the floor of the channel is given by:
τ=2ηv0h
Topper's Solved these Questions
- TEST PAPERSBook:RESONANCE ENGLISHChapter:TEST PAPERSExercise:PART - II PHYSICS
Explore 106 Videos
- SIMPLE HARMONIC MOTION Book:RESONANCE ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:Advanced Level Problems
Explore 13 Videos
- TEST SERIESBook:RESONANCE ENGLISHChapter:TEST SERIESExercise:PHYSICS
Explore 130 Videos
Similar Questions
An incompressible liquid is flowing through a horizontal pipe as shown in figure. The value of speed v is
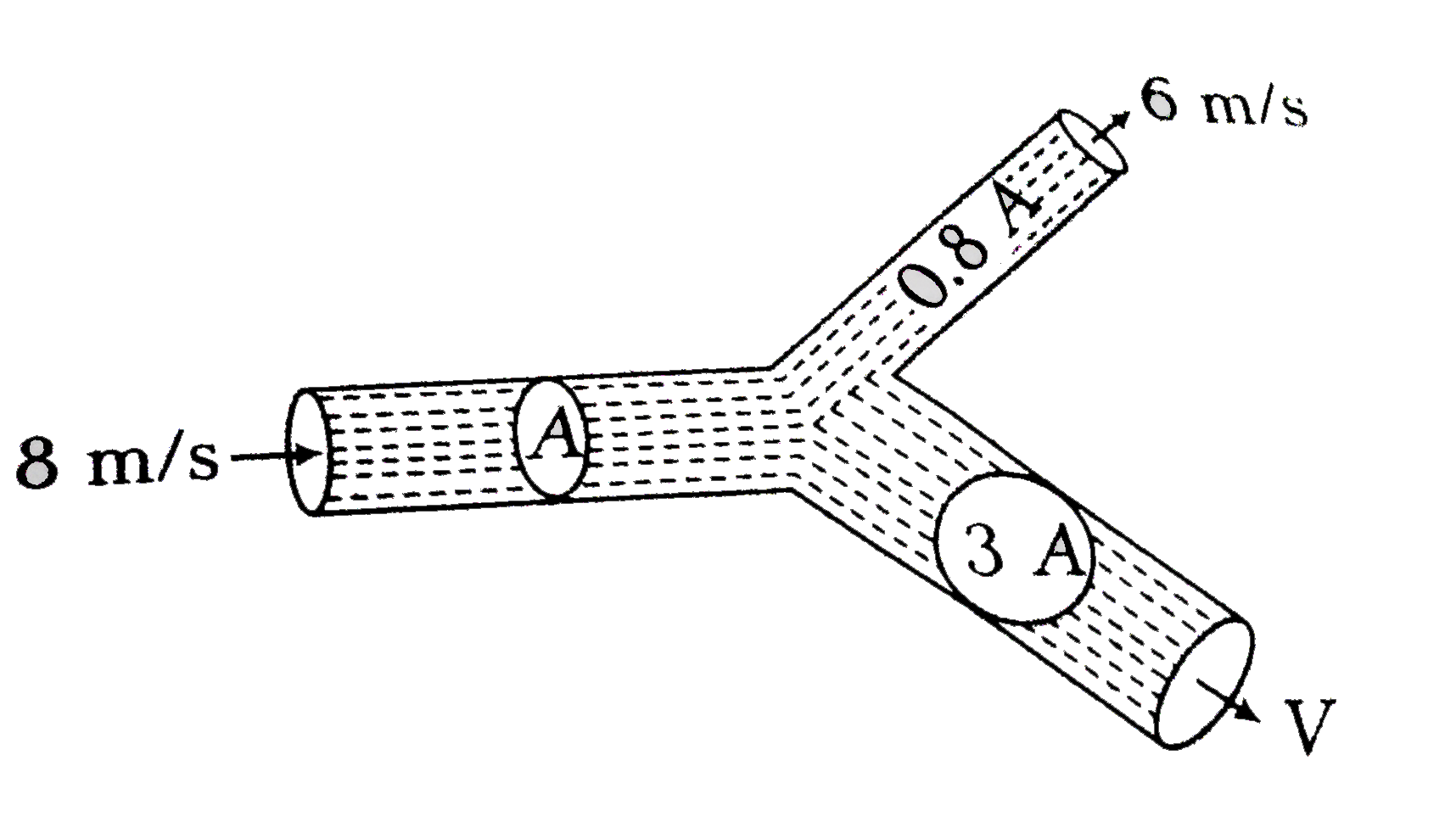
View SolutionA liquid flows through a horizontal tube. The velocities of the liquid in the two sections, which have areas of cross section A1 and A2 are v1 and v2 respectively. The difference in the levels of the liquid in the two vertical tubes is h. Then

View Solution
Knowledge Check
A stone is dropped into a pond from the top of the tower of height h. If v is the speed of sound in air, then the sound of splash will be heard at the top of the tower after a time
A√2hg+hvB√2hg−hvC√2hgD√2hg+2hvA liquid flows through a horizontal tube as shown in figure. The velocities of the liquid in the two sections, which have areas of cross-section A1 and A2 and v1 and v2 respectively. The differnece in the levels of the liquid in the two vertical tubes is h. then
 Av22−v21=2ghBv22+v21=2ghCv22−v21=ghDv22+v21=gh
Av22−v21=2ghBv22+v21=2ghCv22−v21=ghDv22+v21=gh
When a liquid flows in a tube, there is relative motion between adjacent layers of the liquid. This force is called the viscous force which tends to oppose the relative motion between the layers of the liquid. Newton was the first person to study the factors that govern the viscous force in a liquid. According to Newton’s law of viscous flow, the magnitude of the viscous force on a certain layer of a liquid is given by
F=−ηAdvdx
where A is the area of the layer dvdx is the velocity gradient at the layer and η is the coefficient of viscosity of the liquid.
A river is 5 m deep. The velocity of water on its surface is 2ms−1 If the coefficient of viscosity of water is 10−3Nsm−2 , the viscous force per unit area is :
View SolutionA plate of area 2m2 is made to move horizontally with a speed of 2m/s by applying a horizontal tangential force over the free surface of a liquid. If the depth of the liquid is 1m and the liquid in contact with the bed is stationary. Coefficient of viscosity of liquid is 0.01 poise. Find the tangential force needed to move the plate.
View SolutionA plate of area 2m2 is made to move horizontally with a speed of 2m/s by applying a horizontal tangential force over the free surface of a liquid. If the depth of the liquid is 1m and the liquid in contact with the bed is stationary. Coefficient of viscosity of liquid is 0.01 poise. Find the tangential force needed to move the plate.
View Solution
A container filled with viscous liquid is moving vertically downwards with constant speed 3v0. At the instant shown, a sphere of radius r is moving vertically downwards (in liquid) has speed v0. The coefficient of viscosity is η. There is no relative motion between the liquid and the container. Then at the shoen instant, The magnitude of viscous force acting on sphere is
View SolutionA projectile is fired from the origin with a velocity v0 at an angle θ with x-axis. The speed of the projectile at an altitude h is .
View SolutionThe velocity distribution for the flow of a Newtonian fluid between two wide, parallel plates is given by the equation
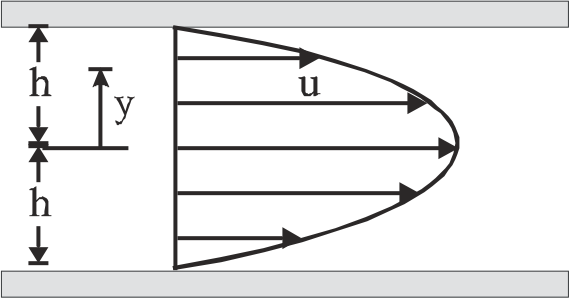
u=3V2[1−(yh)2]
where V is the mean velocity. The fluid has coefficient of viscosity η Answer the following 3 questions for this situation.
Shear stress acting on the bottom wall is
View Solution

