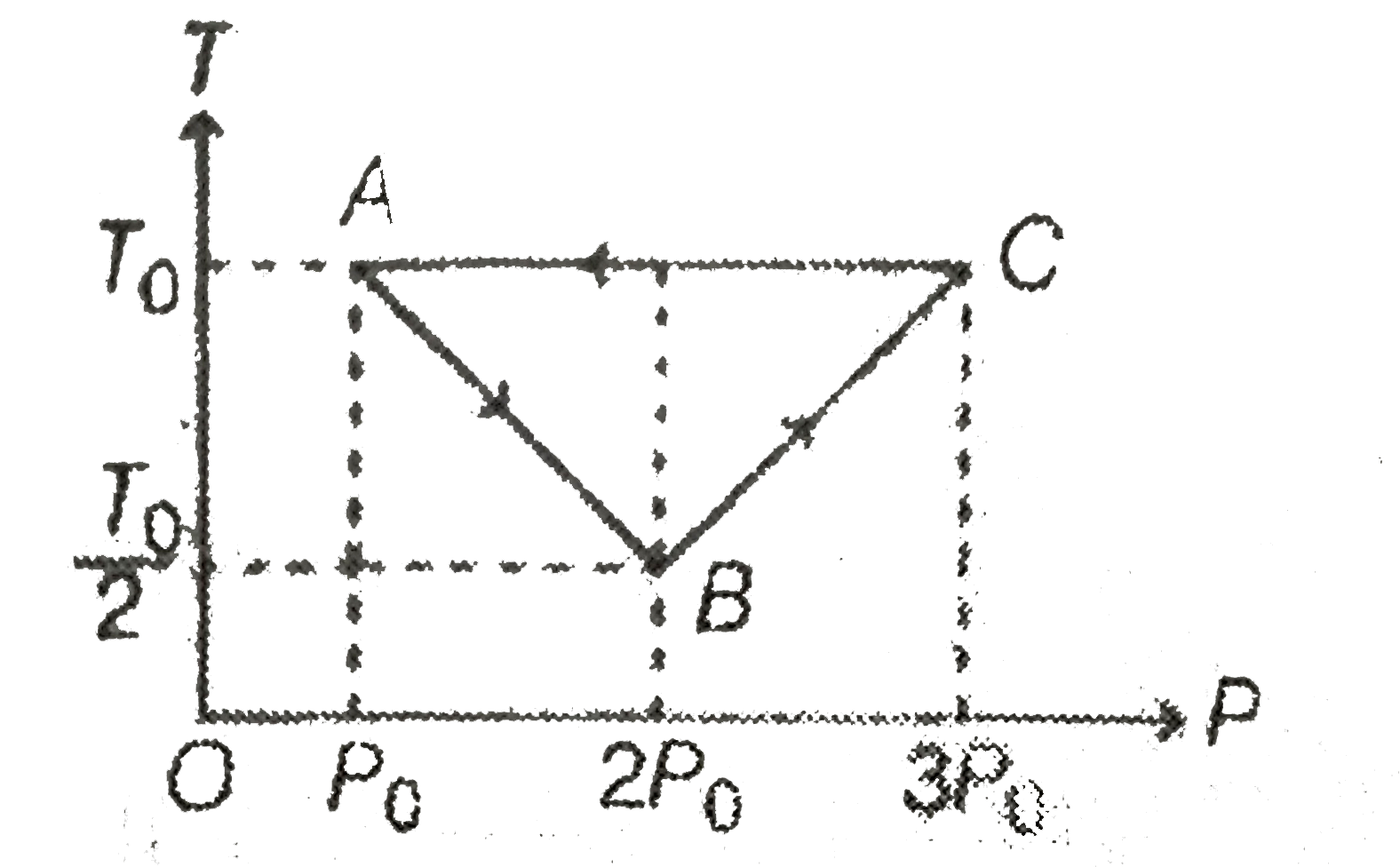
On the P−T graph of an ideal gas, choose the correct option(s):
Adiabatic process will be a straight line.
Isochoric process will be straight line passing through the origin.
adiabatic curve will have a positive slope.
the slope of adiabatic curve is proportional T.
The correct Answer is:B, C
To solve the question regarding the P−T graph of an ideal gas, we will analyze the different processes (adiabatic and isochoric) and their characteristics on the graph.
1. Understanding the Adiabatic Process:
- The adiabatic process for an ideal gas is described by the equation \( PV^{\gamma} = \text{constant} \), where \( \gamma \) is the adiabatic exponent.
- From the ideal gas law, we know \( PV = nRT \). We can express pressure \( P \) in terms of temperature \( T \) and volume \( V \):
\(
P = \frac{nRT}{V}
\)
- Substituting this into the adiabatic equation gives:
\(
\left(\frac{nRT}{V}\right)V^{\gamma} = \text{constant}
\)
- Rearranging, we find:
\(
P \propto T^{\frac{1}{\gamma - 1}}
\)
- This indicates that the relationship between \( P \) and \( T \) is not linear, hence the adiabatic process will not be a straight line on the P−T graph.
2. Analyzing the Isochoric Process:
- In an isochoric process, the volume \( V \) is constant. Thus, the relationship simplifies to:
\(
P \propto T
\)
- This means that for a constant volume, pressure is directly proportional to temperature, which results in a straight line on the P−T graph.
3. Slope of the Adiabatic Curve:
- The slope of the adiabatic curve can be derived from the relationship established earlier. By differentiating the logarithmic form of the relationship, we find:
\(
\frac{dP}{dT} = \frac{\gamma P}{T(\gamma - 1)}
\)
- This shows that the slope depends on both pressure \( P \) and temperature \( T \), and is positive as both \( P \) and \( T \) are positive in the context of ideal gases.
4. Conclusion:
- The adiabatic process does not represent a straight line on the P−T graph.
- The isochoric process does represent a straight line on the P−T graph.
- The slope of the adiabatic curve is not directly proportional to temperature but rather depends on both pressure and temperature.
Final Answer:
- The correct options are:
- B: Isochoric process will be a straight line.
- C: The slope of the adiabatic curve is positive.
- The adiabatic process for an ideal gas is described by the equation \( PV^{\gamma} = \text{constant} \), where \( \gamma \) is the adiabatic exponent.
- From the ideal gas law, we know \( PV = nRT \). We can express pressure \( P \) in terms of temperature \( T \) and volume \( V \):
\(
P = \frac{nRT}{V}
\)
- Substituting this into the adiabatic equation gives:
\(
\left(\frac{nRT}{V}\right)V^{\gamma} = \text{constant}
\)
- Rearranging, we find:
\(
P \propto T^{\frac{1}{\gamma - 1}}
\)
- This indicates that the relationship between \( P \) and \( T \) is not linear, hence the adiabatic process will not be a straight line on the P−T graph.
- In an isochoric process, the volume \( V \) is constant. Thus, the relationship simplifies to:
\(
P \propto T
\)
- This means that for a constant volume, pressure is directly proportional to temperature, which results in a straight line on the P−T graph.
- The slope of the adiabatic curve can be derived from the relationship established earlier. By differentiating the logarithmic form of the relationship, we find:
\(
\frac{dP}{dT} = \frac{\gamma P}{T(\gamma - 1)}
\)
- This shows that the slope depends on both pressure \( P \) and temperature \( T \), and is positive as both \( P \) and \( T \) are positive in the context of ideal gases.
- The adiabatic process does not represent a straight line on the P−T graph.
- The isochoric process does represent a straight line on the P−T graph.
- The slope of the adiabatic curve is not directly proportional to temperature but rather depends on both pressure and temperature.
- The correct options are:
- B: Isochoric process will be a straight line.
- C: The slope of the adiabatic curve is positive.
Similar Questions
Choose the correct option(s)
View SolutionChoose the correct option w.r.t TMV
View SolutionFor the given P-V graph for an ideal gas, chose the correct V-T graph. Process BC is adiabatic.
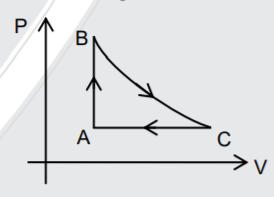
View SolutionChoose the correct option w.r.t RNA.
View SolutionConsidering the graph of 1s , choose the correct option:
View SolutionAn ideal monatomic gas expands in such a way that TV12= constant, where T and V are the temperature & volume of the gas, choose the correct option(s)
View SolutionStudy the given graph and choose the correct option.
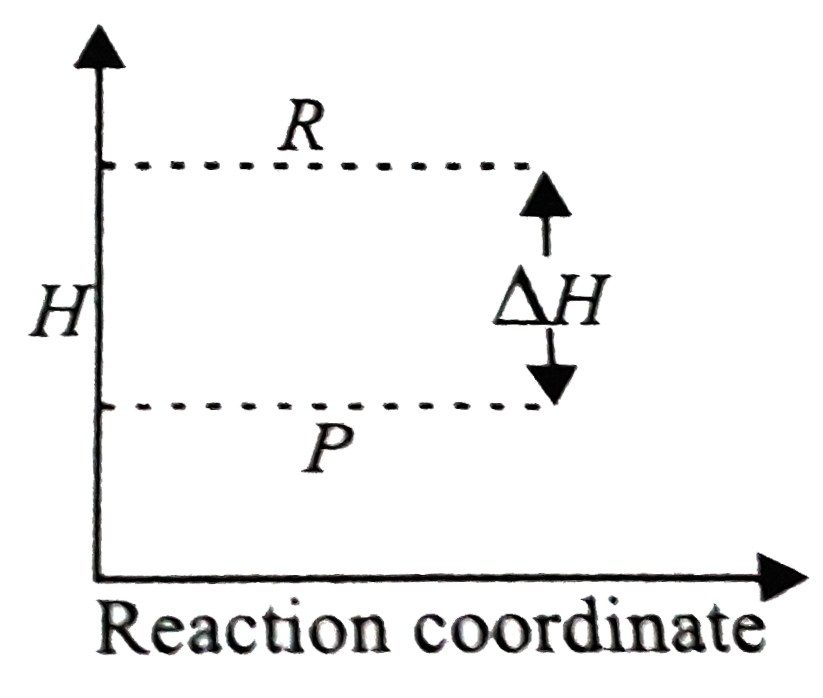
View SolutionForce acting on a block versus time graph is as shown in figure Choose the correct options.(g=10m/s−2)
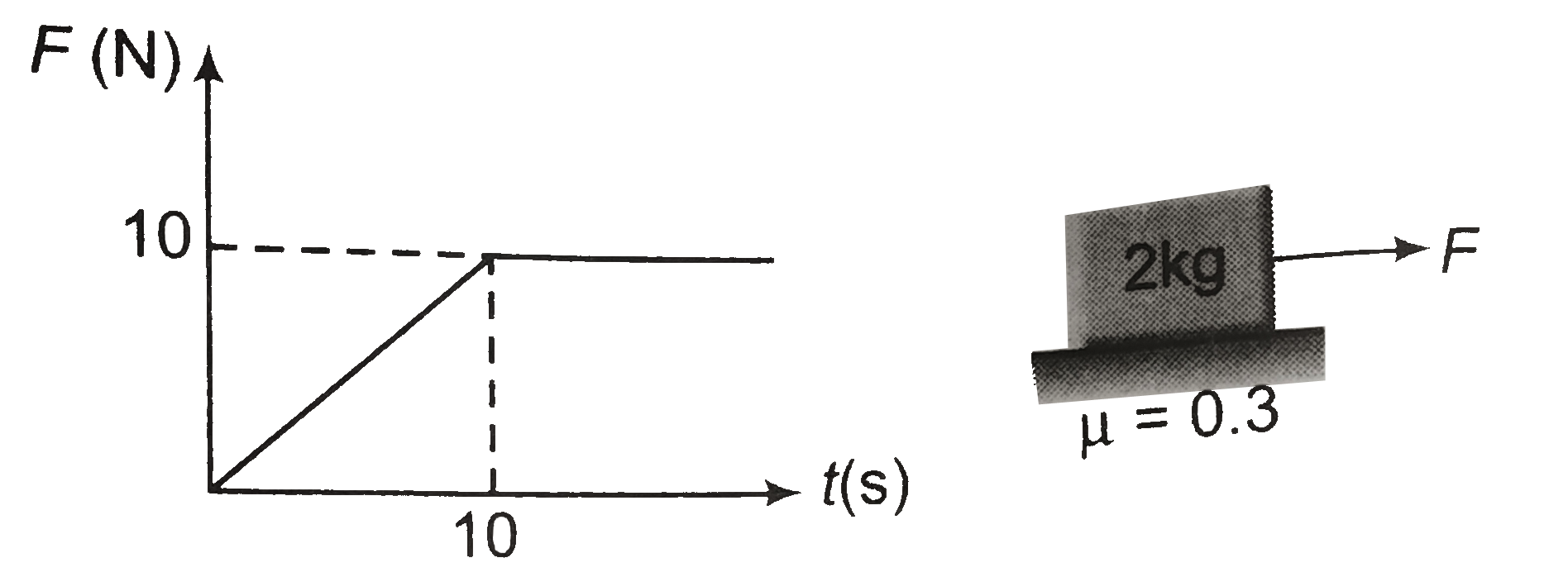
View SolutionIf the switch at point P is opened (which was initially closed), choose the correct option (s).
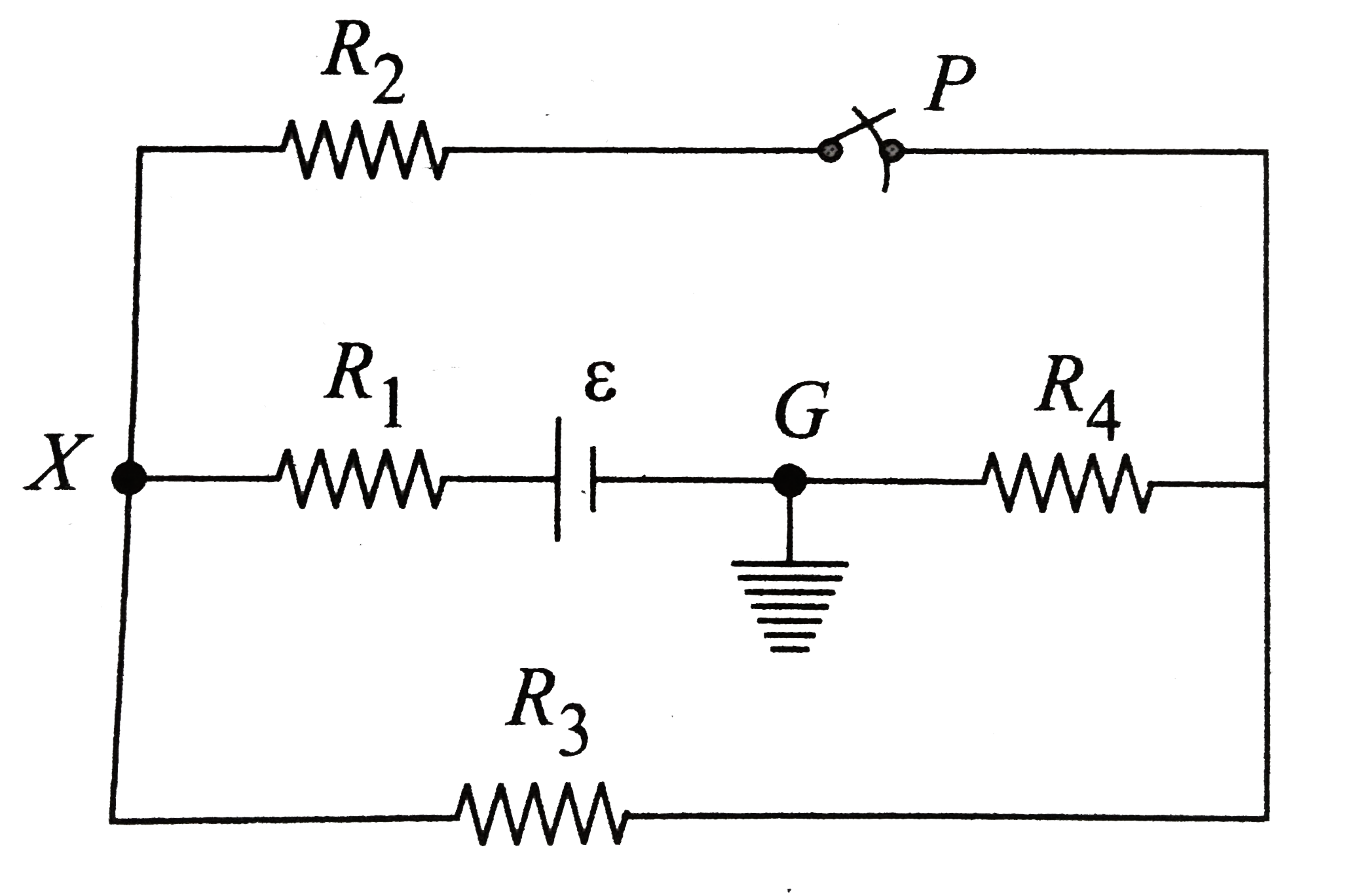
View SolutionOne mole of an ideal monoatomic gas is taken through a cyclic process as shown. Choose the correct option(s).
View Solution

