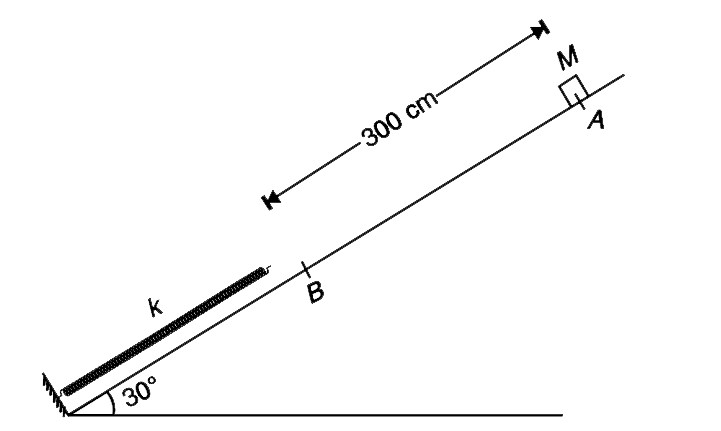
A block of mass M = 40 kg is released on a smooth incline from point A. After travelling through a length of 30 cm it strikes an ideal spring of force constant $K = 1000 N / m$ . It compresses the spring and then gets pushed back. How much time after its release, the block will be back to point A?

A

$4 sec$ .

B

$2.5 sec .$

C

$1.54 sec$ .

D

$3.26 sec$ .

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Time to travel from $A$ to $B (t_{1})$ is given by -
$x = u t + \frac{1}{2} a t^{2}, [∴ a = g sin θ = 5 m / s^{2}]$
$0.3 = \frac{1}{2} \times 5 \times t_{1}^{2} \Rightarrow t_{1} = 0.35 s$
Speed of the block when it hits the spring is given by -
$V^{2} = 0^{2} + 2 a x = 2 \times 5 \times 0.3$
$V = \sqrt{3} m / s$
The motion of the block in contact with the spring can be regarded as a part of $S H M$ . In equilibrium, compression in the spring is given by
$k x_{0} = m g sin θ$
$x_{0} = \frac{40 \times 10 \times \frac{1}{2}}{1000} = 0.2 m$
Let the block compress the spring by a length $x_{1}$ .
Energy conservation gives -
$\frac{1}{2} k x_{1}^{2} = \frac{1}{2} M V^{2} + M g x_{1} sin θ$
$\frac{1}{2} \times 1000 . x_{1}^{2} = \frac{1}{2} \times 40 \times {(\sqrt{3})}^{2} \times (40 \times 10 \times \frac{1}{2}) x_{1}$
$5 x_{1}^{2} - 2 x_{1} - 0.6 m$
Solving $x_{1} = 0.5 m$
Hence, amplitude of $S H M$ is $A = x_{1} - x_{0} = 0.4 m$

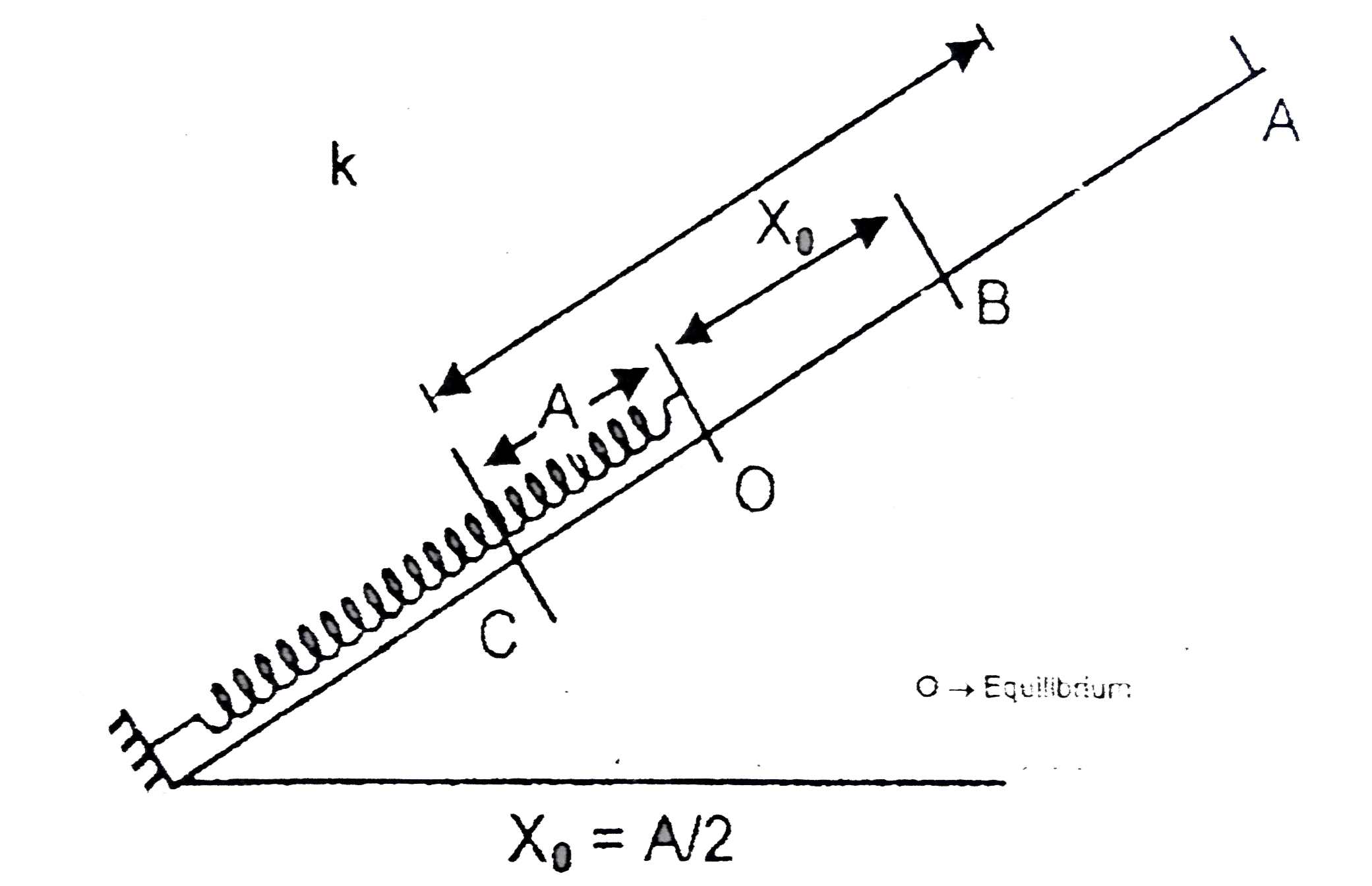
The motion from $B$ to $C$ and back to $B$ can be regarded as motion of a particle performing $S H M$ [from $x = + \frac{A}{2}$ to negative extrem e and back to $x = + \frac{A}{2}$ ]
Time for this motion can be obtained from fig given below.

Particle on circle moves from $P_{1}$ to $C$ to $P_{2}$ . Time required
for completing this two third circle $= \frac{2 T}{3}$
Hence, desired time $t_{2} = \frac{2 T}{3} = \frac{2}{3} 2 π \sqrt{\frac{m}{k}}$
$= \frac{4 π}{3} \sqrt{\frac{40}{1000}} l = \frac{8 π}{30} s = 0.84 s$
$∴$ Time required for the block to come back to $A$ is $t = 2 t_{1} + t_{0}$
$= 2 \times 0.35 + 0.84 = 1.54 s$

Updated on:21/07/2023

|

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

RESONANCE ENGLISH-TEST PAPERS-PHYSICS

Home
Ask Doubt
Profile