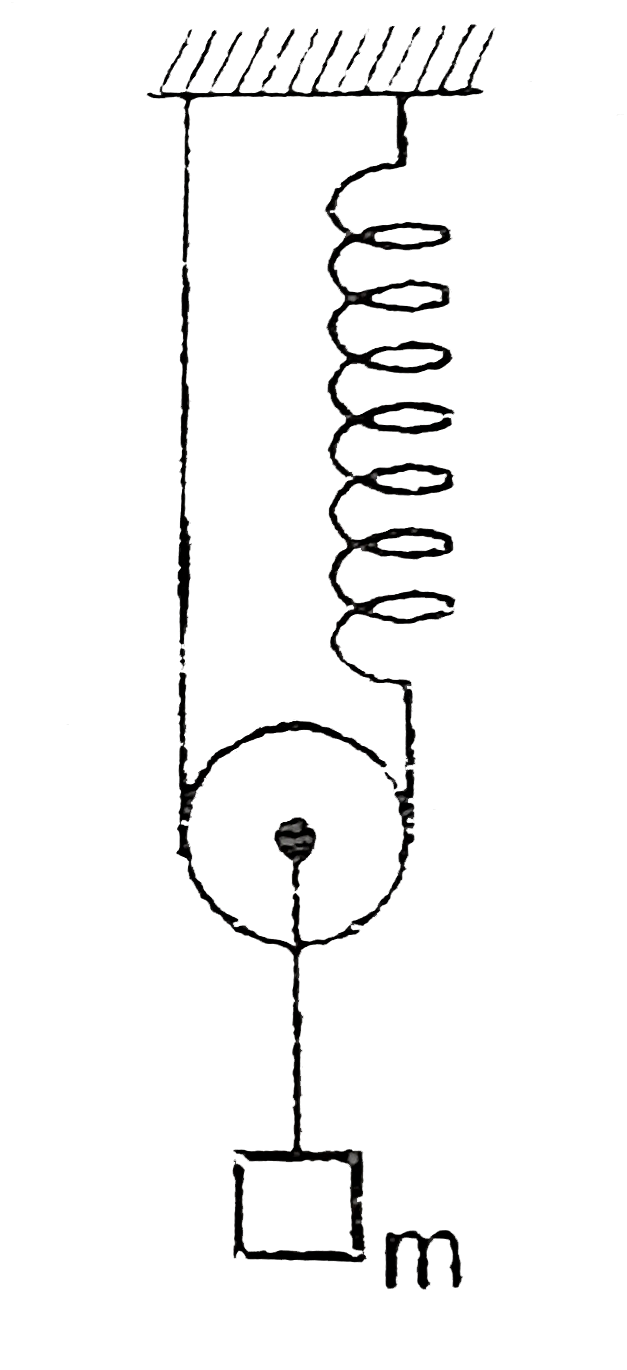
The system is released from rest with spring intially in its natural length. If mass of the block m = 10 kg. and spring constant k=100N/m, then maximum extension in spring is :
1 m
12m
2 m
2.5 m
The correct Answer is:A
Let maximum elongation in spring be X, then block descends through x2
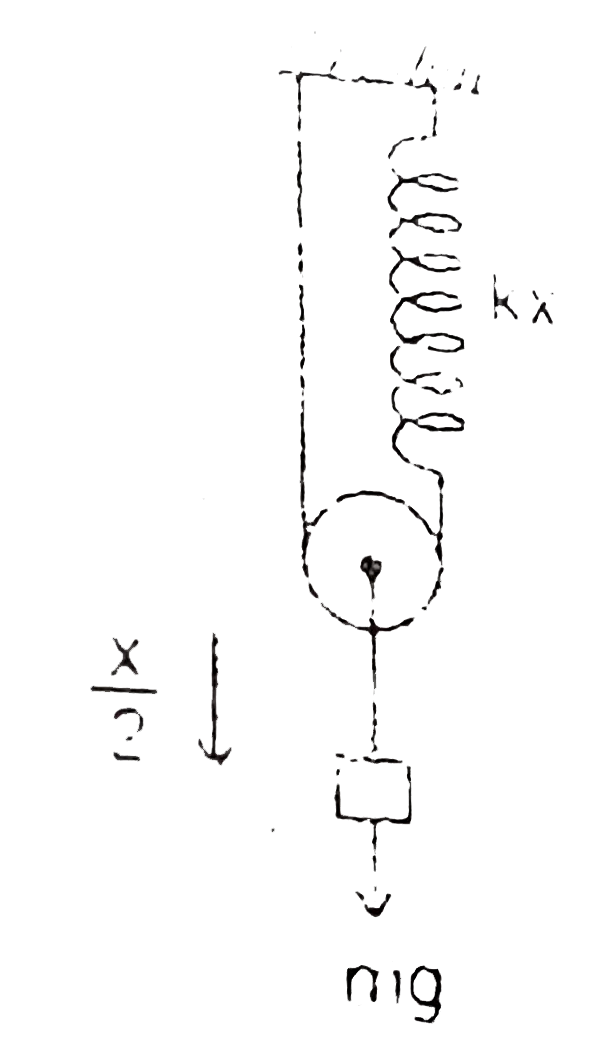
BY WET
mgx2−12kx2=0⇒X=mgk=10×10100=1m
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.67
10 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.68
9 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.65
9 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
19 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
The system is released from rest with both the springs in unstretched positions. Mass of each block is 1 kg and force constant of each spring is 10N/m.
Extension of horizontal spring in equilibrium is
View SolutionInitially spring is in natural length and both blocks are in rest condition. Then deter mine
maximum extension in spring . K = 20 N/M
View SolutionThe system is released from rest with both the springs in unstretched positions. Mass of each block is 1 kg and force constant of each spring is 10N/m.
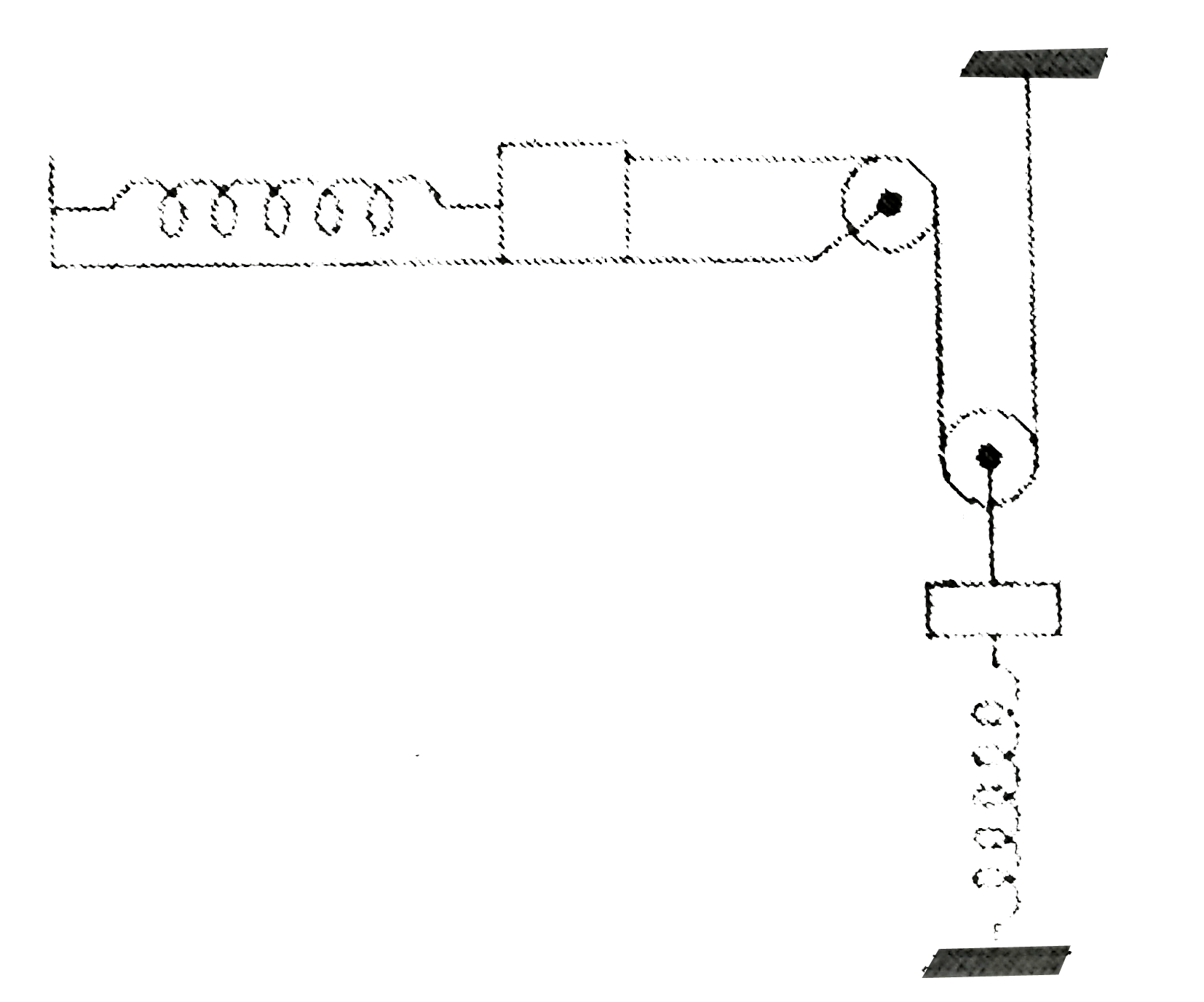
In the equilibrium position, speed of the block placed horizontally is
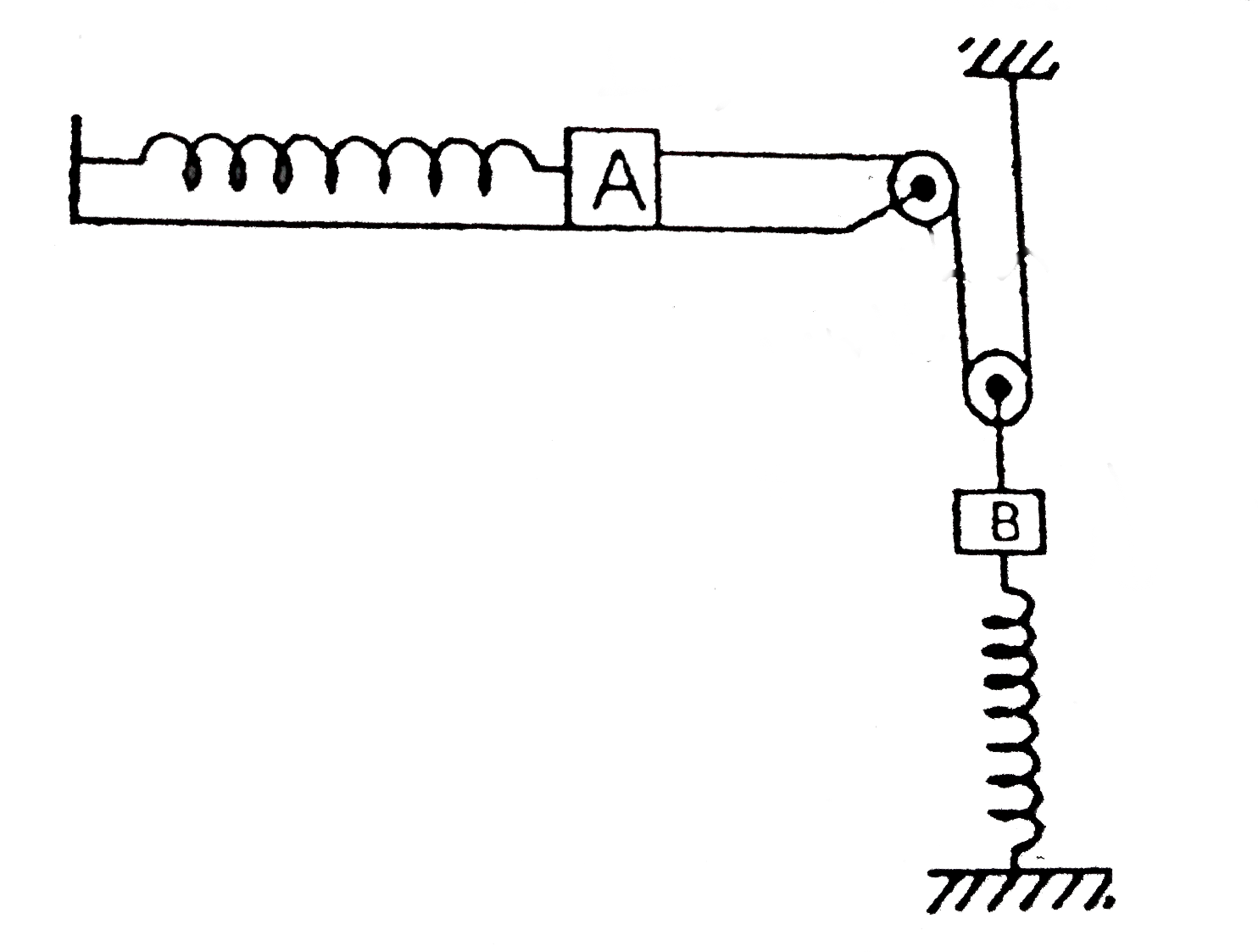
View SolutionThe system is released from rest with both the springs in unstretched positions. Mass of each block is 1kg and force constant of each spring is 10N/m. Then choose the incorrect option(s). Assume puleys and strings are massless and all contacts are smooth. (g=10m/s2)
View SolutionA block of mass m is attached with a spring in vertical plane as shown in the figure. If initially spring is in its natural length and the block is released from rest, then maximum extension in the spring will be
View SolutionBlocks A and B shown in the figure are having equal masses m. The system is released from rest with the spring unstretched. The string between A and ground is cut, when there is maximum extension in the spring. The acceleration of centre of mass of the two blocks at this instant is
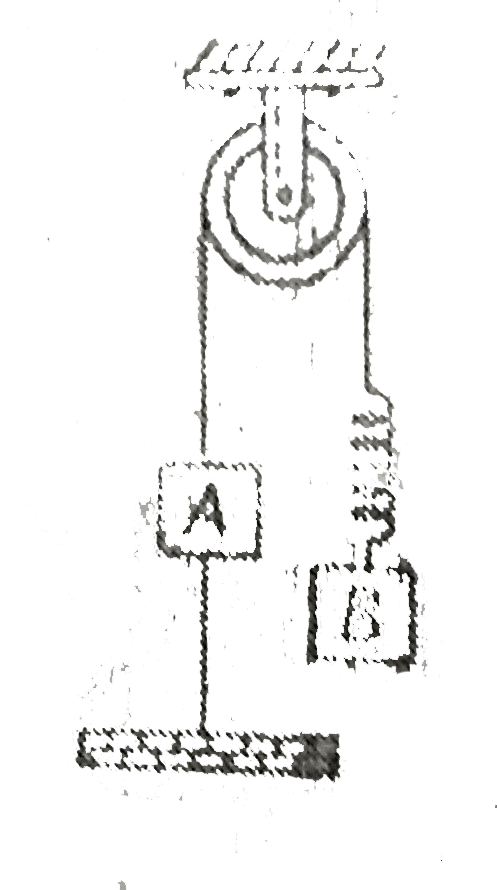
View SolutionFind the maximum tension in the spring if initially spring at its natural length when block is released from rest.

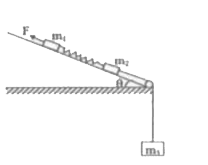
View SolutionTwo blocks of masses m1=2kg and m2=4kg are attached to two ends of a light ideal spring of force constant k = 1000 N/m. The system is kept on a smooth inclined plane inclined at 30∘ with horizontal. The block m2 is attached to a light string whose other end is connected to a mass m3=1kg. A force F = 15N is applied on m1 and the system is released from rest. Assume initially the spring is at relaxed position and the system is released from rest. Find the
(a) maximum extension of the spring.
(
View SolutionConsider the situation shown in figure.
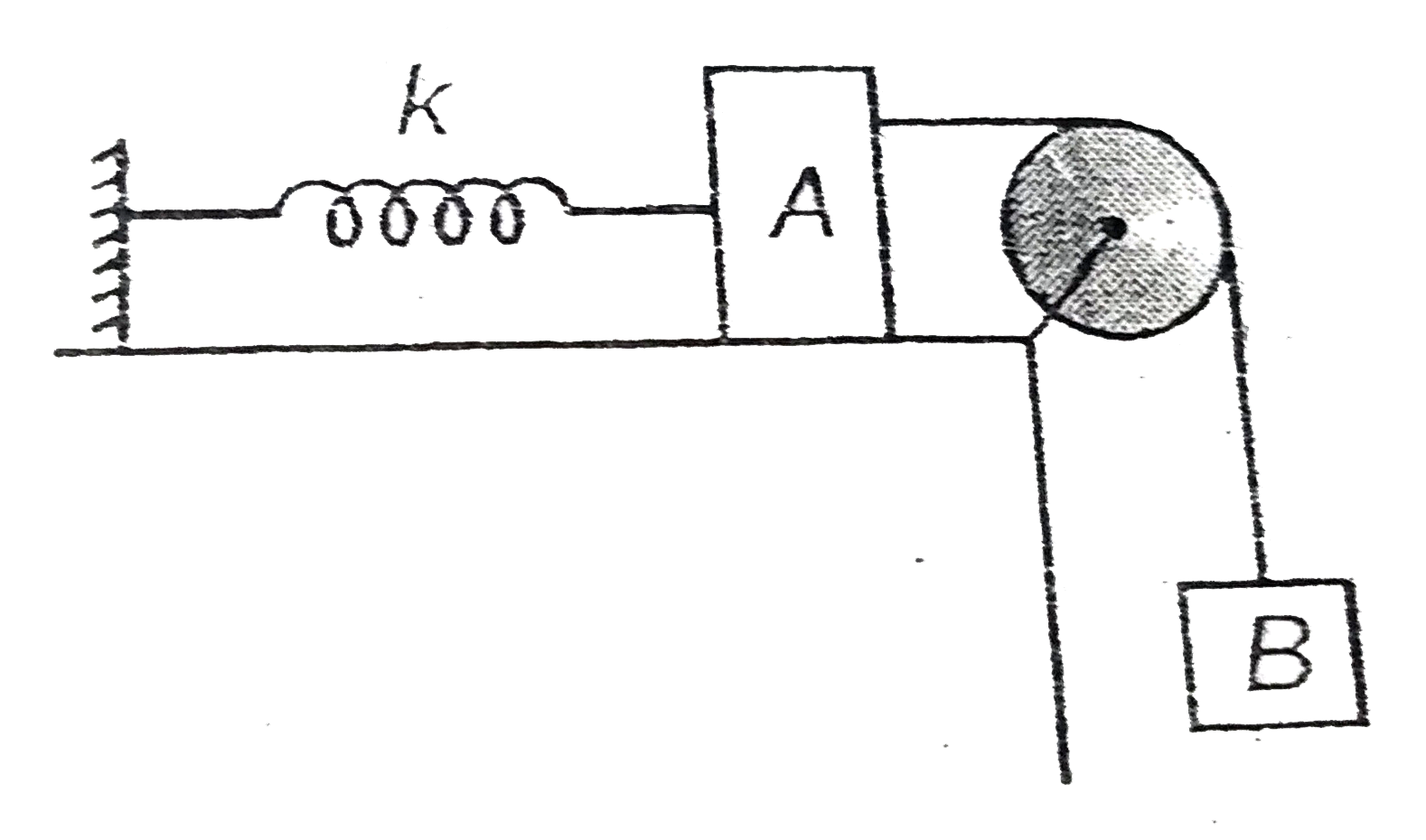
Mass of block A is m and that of blcok B is 2m. The force constant of string is k. Friction is absent everywhere. System is released from rest with the spring unstretched. Find
(a) The maximum extension of the spring xm
(b) The speed of block A when the extension in the springt is x=xm2
(c ) The net acceleration of block B when extension in the spring is x=xm4.
View SolutionBlock A of mass m is placed on a plank B. A light support S is fixed on plank B and is attached with the block A with a spring of spring constant K. Consider that initially spring is in its natural length. If the plank B is given an acceleration a, then maximum compression in the spring is xmak. Find the value of x (All the surface are smooth)

View Solution
