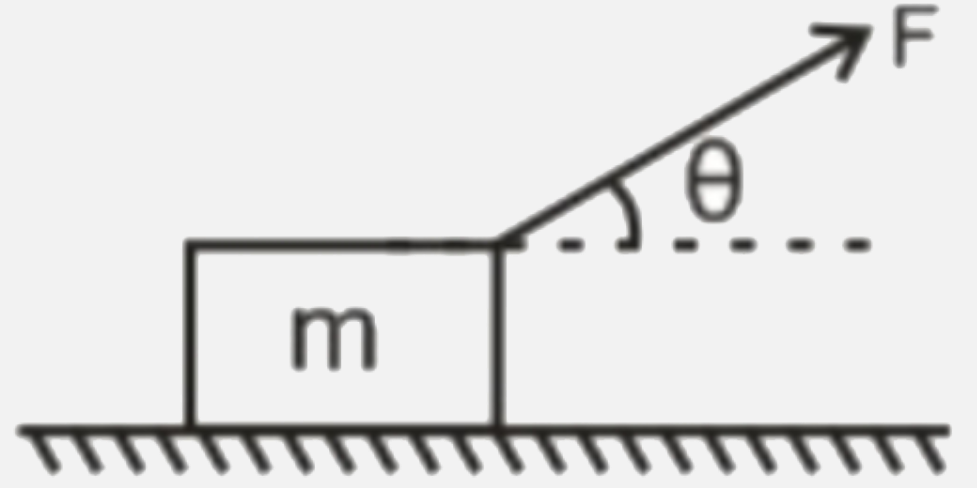
A wooden block of mass m resting on a rough horizontal table is pulled by a force F as shown in the figure. If μ is the coefficient of friction between block and table, its acceleration will be
√168N
√174N
√194N
None of these
The correct Answer is:B
Acceleration of the platform
→ap−d→vdt−2ˆi+ˆj+3ˆk
Horizontal force on the block
Normal force on the block
aH=√4+1=√5m/s2
av=3m/s2
Normal force on the block
N=m(g+av)=1×13=13N
Maximum acceleration that friction can positive
amass=μ(g+ay)=0.2×13=206m/s2
∴amax>aH
∴ Value of frication force on the block
f=maH=√5N
∴ Force by the platform on the block is
F=√N2t2=√169+5=√174N
Topper's Solved these Questions
- TEST PAPERSBook:RESONANCE ENGLISHChapter:TEST PAPERSExercise:PART - II PHYSICS
Explore 106 Videos
- SIMPLE HARMONIC MOTION Book:RESONANCE ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:Advanced Level Problems
Explore 13 Videos
- TEST SERIESBook:RESONANCE ENGLISHChapter:TEST SERIESExercise:PHYSICS
Explore 130 Videos
Similar Questions
A wooden block of mass M resting on a rough horizontal surface is pulled with a force T at an angle q to the horizontal. If m is coefficient of kinetic friction between the block and the surface, the acceleration of the block is
View SolutionA block of mass m slides in right angled incliine through as shown in the figure . If the coefficient of kinetic friction between the block and the through is μk , find the acceleration of the block .

View Solution
Knowledge Check
A block of mass m=2kg is resting on a rough inclined plane of inclination of 30∘ as shown in figure. The coefficient of friction between the block and the plane is μ=0.5. What minimum force F should be applied perpendicular to the plane on the block, so that blocks does not slip on the plane? (g=10m/s2)
 A2.68 NBZeroC4.34 ND6.24 N
A2.68 NBZeroC4.34 ND6.24 NA 20 N block is being pushed across a horizontal table by an 18 N force. If the coefficient of kinetic friction between the block and the table is 0.4, find the acceleration of the block.
A0.5m/s2B1m/s2C5m/s2D7.5m/s2Two blocks A and B of masses 10 kg and 15 kg are placed in contact with each other rest on a rough horizontal surface as shown in the figure. The coefficient of friction between the blocks and surface is 0.2. A horizontal force of 200 N is applied to block A. The acceleration of the system is (Take g=10ms−2)
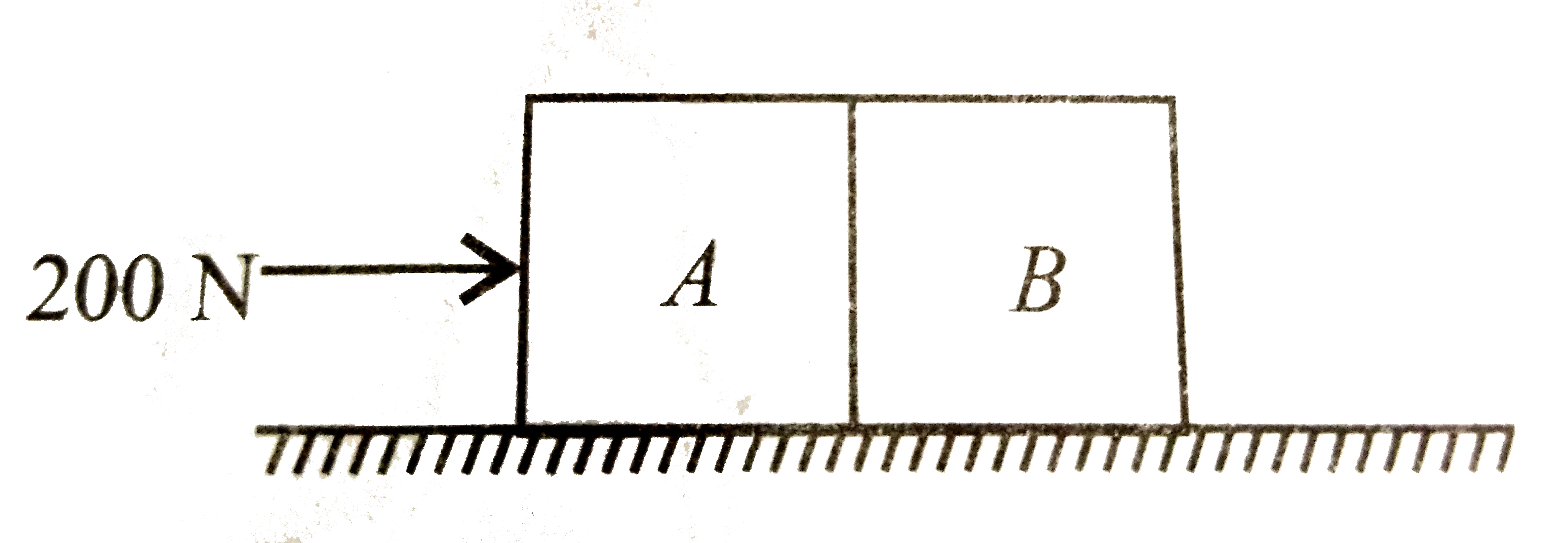 A4ms−2B6ms−2C8ms−2D10ms−2
A4ms−2B6ms−2C8ms−2D10ms−2
A block of mass m is stationary on a rough inclined plane making an angle θ with the horizontal. Find the contact force between block and the plane
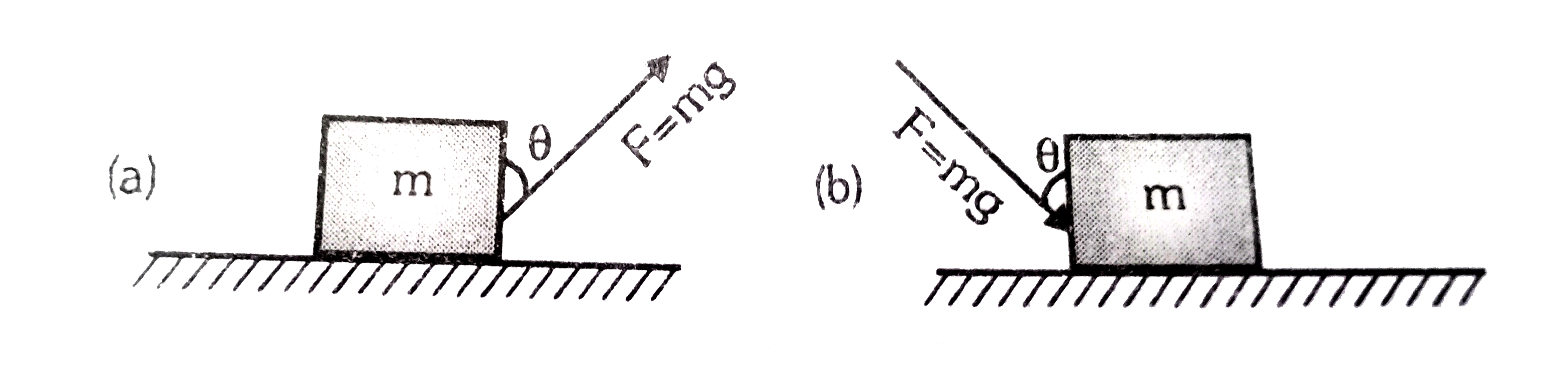
View SolutionA block of mass m rests on a rough horizontl surface as shown in figure (a) and (b). Coefficient of friciton between block and surface is μ. A force F-mg acting at an angle θ with the vertical side of the block. Find the condition for which block will move along the surface.
View SolutionA block on table shown in figure is just on the wedge of slipping. Find the coefficient of static friction between the block and table top.

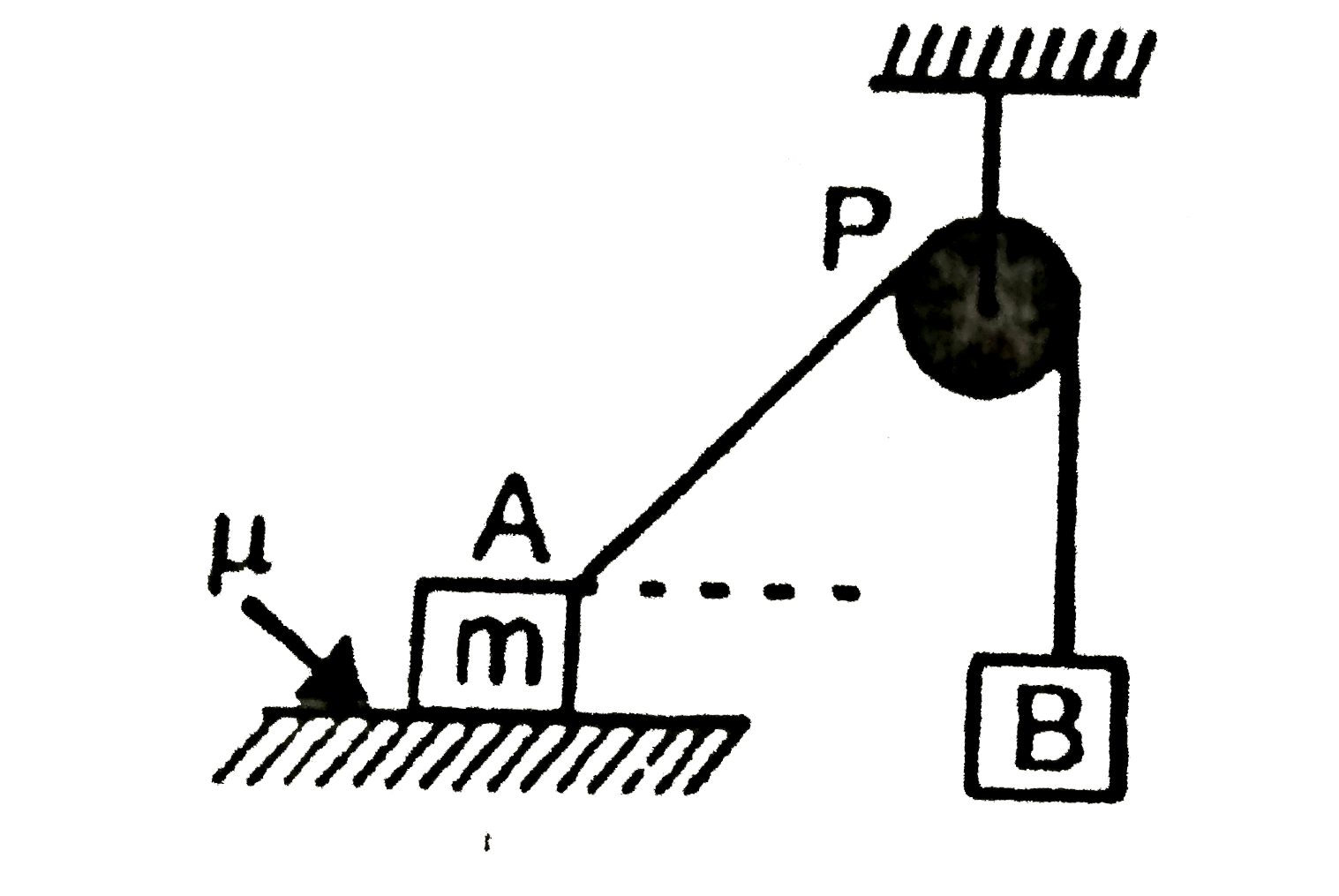
View SolutionIn figure shown minimum mass of block B( at a particular angle between horizontal and string AP) to just slide the block A on rough horizontal surface is m2 as shown in figure. If μ is the coefficient of friction between block A and ground then pμ2 will be :
View SolutionA block of mass m kept on rough horizontal turn table at a distance x from the centre. If the coefficient of friction between the table and block is μ then maximum speed of point P on turn table so that the block does not slip is

View Solution