A particle is attached to an end of a rigid rod. The other end of the rod is hunged and the rod rotates always remaining horizontal. Its angular speed is increasing at contant rate. The mass of the particle is m . The force exerted by the rod on the particle is →F , then:
F≥mg
F is constant
The angle between →F and horizontal plane decreases
The angle between →F and the rod decreases
To solve the problem, we need to analyze the forces acting on the particle attached to the end of the rigid rod. The rod is rotating in a horizontal plane, and the angular speed is increasing at a constant rate.
1. Identify the Forces Acting on the Particle:
- The particle has two main forces acting on it:
- The gravitational force →Fg=m→g acting downwards (where g is the acceleration due to gravity).
- The force exerted by the rod on the particle, denoted as →F.
2. Understand the Motion of the Rod:
- As the rod rotates, it maintains a horizontal position. The angular speed is increasing, which means the particle is undergoing angular acceleration.
- The centripetal force required for circular motion is provided by the horizontal component of the force →F.
3. Analyze the Components of the Forces:
- The force →F can be resolved into two components:
- A vertical component Fv that balances the weight of the particle: Fv=mg.
- A horizontal component Fh that provides the necessary centripetal force for circular motion.
4. Centripetal Force Requirement:
- The centripetal force Fh is given by Fh=mv2r, where v is the tangential speed of the particle and r is the radius of the circular path (length of the rod).
5. Relationship Between Forces:
- Since the rod is rotating with increasing angular speed, the angle θ between the force →F and the vertical will change over time. As the angular speed increases, the horizontal component of the force must increase to provide the necessary centripetal force.
6. Conclusion About the Force and Angle:
- As the angular speed increases, the angle θ between the force →F and the vertical decreases. This means that the force exerted by the rod on the particle is not constant and the resultant force's direction shifts towards the horizontal as the angular speed increases.
Final Result:
The correct conclusion is that the angle between the force exerted by the rod and the vertical decreases as the angular speed of the rod increases.
- The particle has two main forces acting on it:
- The gravitational force →Fg=m→g acting downwards (where g is the acceleration due to gravity).
- The force exerted by the rod on the particle, denoted as →F.
- As the rod rotates, it maintains a horizontal position. The angular speed is increasing, which means the particle is undergoing angular acceleration.
- The centripetal force required for circular motion is provided by the horizontal component of the force →F.
- The force →F can be resolved into two components:
- A vertical component Fv that balances the weight of the particle: Fv=mg.
- A horizontal component Fh that provides the necessary centripetal force for circular motion.
- The centripetal force Fh is given by Fh=mv2r, where v is the tangential speed of the particle and r is the radius of the circular path (length of the rod).
- Since the rod is rotating with increasing angular speed, the angle θ between the force →F and the vertical will change over time. As the angular speed increases, the horizontal component of the force must increase to provide the necessary centripetal force.
- As the angular speed increases, the angle θ between the force →F and the vertical decreases. This means that the force exerted by the rod on the particle is not constant and the resultant force's direction shifts towards the horizontal as the angular speed increases.
The correct conclusion is that the angle between the force exerted by the rod and the vertical decreases as the angular speed of the rod increases.
Topper's Solved these Questions
Similar Questions
Two particles of mass m each are attached to a light rod of length d, one at its centre and the other at a free end, The rod is fixed at the other end and is rotated in a plane at an angular speed ω. Calculate the angular momentum of the particle at the end with respect to the particle at the centre
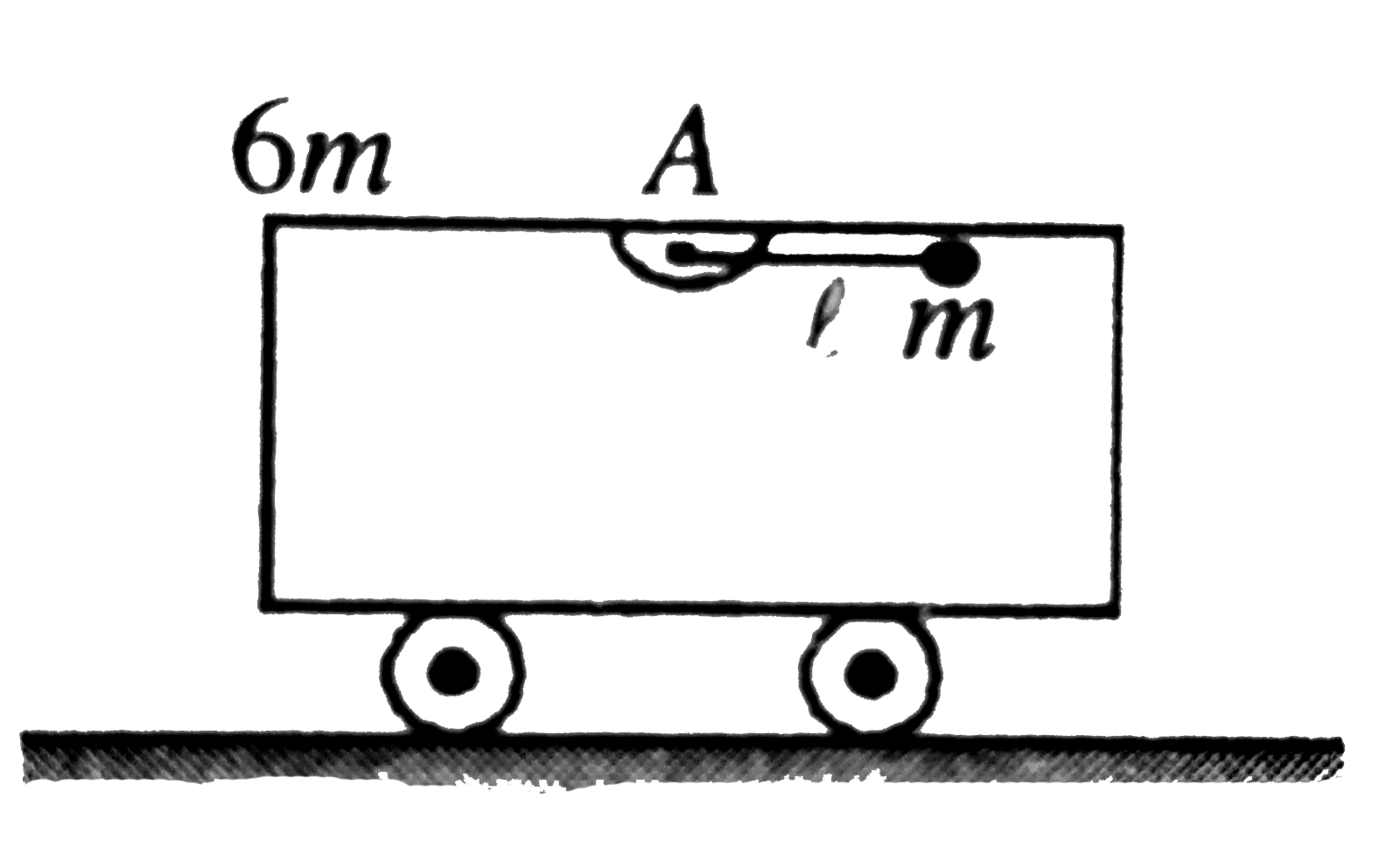
View SolutionIn the figure shown, the cart of mass 6m is initially at rest. A particle of mass in is attached to the end of the light rod which can rotate freely about A. If the rod is released from rest in a horizontal position shown, determine the velocity vrel of the particle with respect to the cart when the rod is vertical.
 View Solution
View SolutionA particle of mass of mass m is attached to a light rod of lenght l other end of the rod is hinged to a wall . Minimumm velocity (Vo) that should be given to a particle in lowest positiion so that it completes a vertical circle
View SolutionA 10kg ball attached at the end of a rigid massless rod of lengh 1m rotates at constant speed in a horizontal circle of radius 0.5m and period of 1.58s , as shown in the figure. The force exerted by the rod on the ball is (g=10ms−2)
 View Solution
View SolutionTwo particles , each of mass m and charge q, are attached to the two ends of a light rigid rod of length 2R . The rod is rotated at constant angular speed about a perpendicular axis passing through its centre. The ratio of the magnitudes of the magnetic moment of the system and its angular momentum about the centre of the rod is
View SolutionTwo particles , each of mass m and charge q, are attached to the two ends of a light rigid rod of length 2R . The rod is rotated at constant angular speed about a perpendicular axis passing through its centre. The ratio of the magnitudes of the magnetic moment of the system and its angular momentum about the centre of the rod is
View SolutionA rod AB of mass m and length L is rotating in horizontal plane about one of its ends which is pivoted. The constant angular speed with which the rod is rotating is ω. The force applied on the rod by the pivot is
View SolutionA uniform rod is hinged at its one end and is allowed to rotate in verticle plANE. Rod is given angular velocity ω in its verticle position as shown in figure. The value of ω for the force exerted by the hinge on rod is zero in this position is
 View Solution
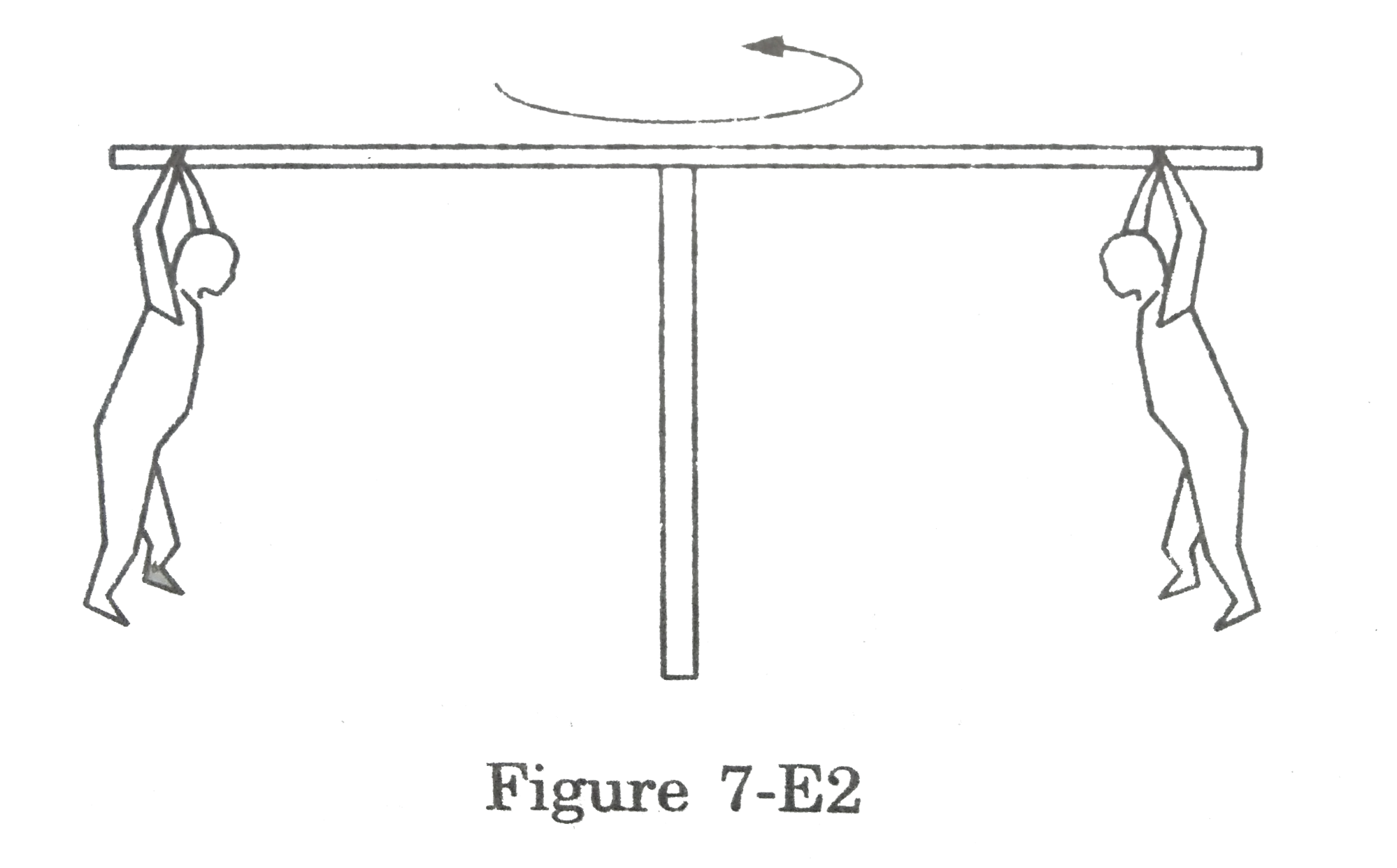
View SolutionIn a children's park a heavy rod is pivoted at the centre and is made to rotate about the pivot so that the rod always remains horizontal. Two kids hold the rod near the ends and thus rotate with the rod figure. Let the mas of each kid be 15 kg, the distance between the points of the rod where the two kids hold it be 3.0 m and suppose that the rod rotates at the rate of 20 revolutions per minute. Find the force of friction exerted by the rod on one of the kids.
 View Solution
View SolutionOne end of a uniform rod of mas m and length l is clamped. The rod lies on a smooth horizontal surface and rotates on it about the clamped end at a uniform angular velocity ω. The force exerted by the clamp on the rod has a horizontal component
View Solution
