Two blocks of masses m1=10kg and m2=20kg are connected by a spring of stiffness k = 200 N/m. The coefficient of friction between the blocks and the fixed horizontal surface is μ=0.1. Find the minimum constant horizontal force F (in Newton) to be applied to m1 in order to slide the mass m2. (Take g=10m/s2)
To find the minimum constant horizontal force F that needs to be applied to mass m1 in order to slide mass m2, we will go through the following steps:
Step 1: Calculate the normal forces on both blocks
The normal force N1 acting on block m1 and N2 acting on block m2 can be calculated using the formula:
N1=m1g
N2=m2g
Given:
- m1=10kg
- m2=20kg
- g=10m/s2
Calculating:
N1=10×10=100N
N2=20×10=200N
Step 2: Calculate the limiting friction forces
The limiting friction force f1 acting on m1 and f2 acting on m2 can be calculated using:
f1=μN1
f2=μN2
Where μ=0.1.
Calculating:
f1=0.1×100=10N
f2=0.1×200=20N
Step 3: Determine the force required to overcome the friction on m2
To slide m2, the force exerted by the spring Fs must at least equal the limiting friction f2:
Fs=f2=20N
Step 4: Relate the spring force to the extension
The spring force Fs can be expressed in terms of the spring constant k and the extension x:
Fs=kx
Where k=200N/m. Setting Fs=20N:
200x=20
Solving for x:
x=20200=0.1m
Step 5: Calculate the work done by the applied force and friction
The work done by the applied force F and the work done against friction must equal the work done on the spring:
F⋅x−f2⋅x=12kx2
Substituting x=0.1m:
F⋅0.1−20⋅0.1=12⋅200⋅(0.1)2
Calculating:
F⋅0.1−2=1
F⋅0.1=3
F=30.1=30N
Conclusion
Thus, the minimum constant horizontal force F that must be applied to m1 in order to slide m2 is:
30N
The normal force N1 acting on block m1 and N2 acting on block m2 can be calculated using the formula:
N1=m1g
N2=m2g
Given:
- m1=10kg
- m2=20kg
- g=10m/s2
N1=10×10=100N
N2=20×10=200N
The limiting friction force f1 acting on m1 and f2 acting on m2 can be calculated using:
f1=μN1
f2=μN2
Where μ=0.1.
f1=0.1×100=10N
f2=0.1×200=20N
To slide m2, the force exerted by the spring Fs must at least equal the limiting friction f2:
Fs=f2=20N
The spring force Fs can be expressed in terms of the spring constant k and the extension x:
Fs=kx
Where k=200N/m. Setting Fs=20N:
200x=20
Solving for x:
x=20200=0.1m
The work done by the applied force F and the work done against friction must equal the work done on the spring:
F⋅x−f2⋅x=12kx2
Substituting x=0.1m:
F⋅0.1−20⋅0.1=12⋅200⋅(0.1)2
Calculating:
F⋅0.1−2=1
F⋅0.1=3
F=30.1=30N
Thus, the minimum constant horizontal force F that must be applied to m1 in order to slide m2 is:
30N
Topper's Solved these Questions
Similar Questions
Two blocks of masses m1 and m2 are connected by a spring of stiffness k. The coefficient of friction between the blocks and the surface is μ. Find the minimum constant force F to be applied to m1 in order to just slide the mass m2.
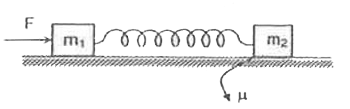
View SolutionTwo block of masses m1 and m2 connected by a light spring rest on a horizontal plane. The coefficient of friction between the block and the surface is equal to μ. What minimum constant force has to be applied in the horizontal direction to the block of mass m1 in order to shift the other block?
View SolutionTwo block of masses m1 and m2 connected by a light spring rest on a horixontal plane. The cofficient of friction between the block and the surface is equal to μ. What minimum constant force has to be applied in the horizontal direction to the block of mass m1 in order to shift the other block?
View SolutionTwo blocks of masses m1=1kg and m2 = 2kg are connected by a spring of spring constant k = 24 N/m and placed on a frictionless horizontal surface. The block m1 is imparted an initial velocity v0 = 12cm/s to the right. The amplitude of oscillation is
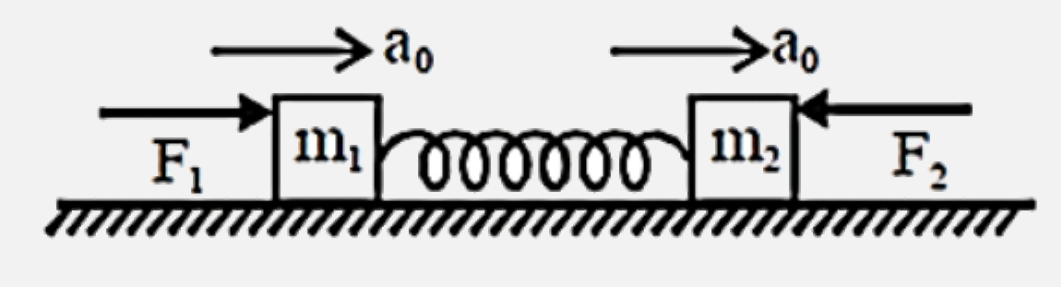
View SolutionTwo blocks of masses m1andm2 being connected with a light spring of stiffness k are driven with forces F1andF2 on a smooth plane .find the value of spring force .
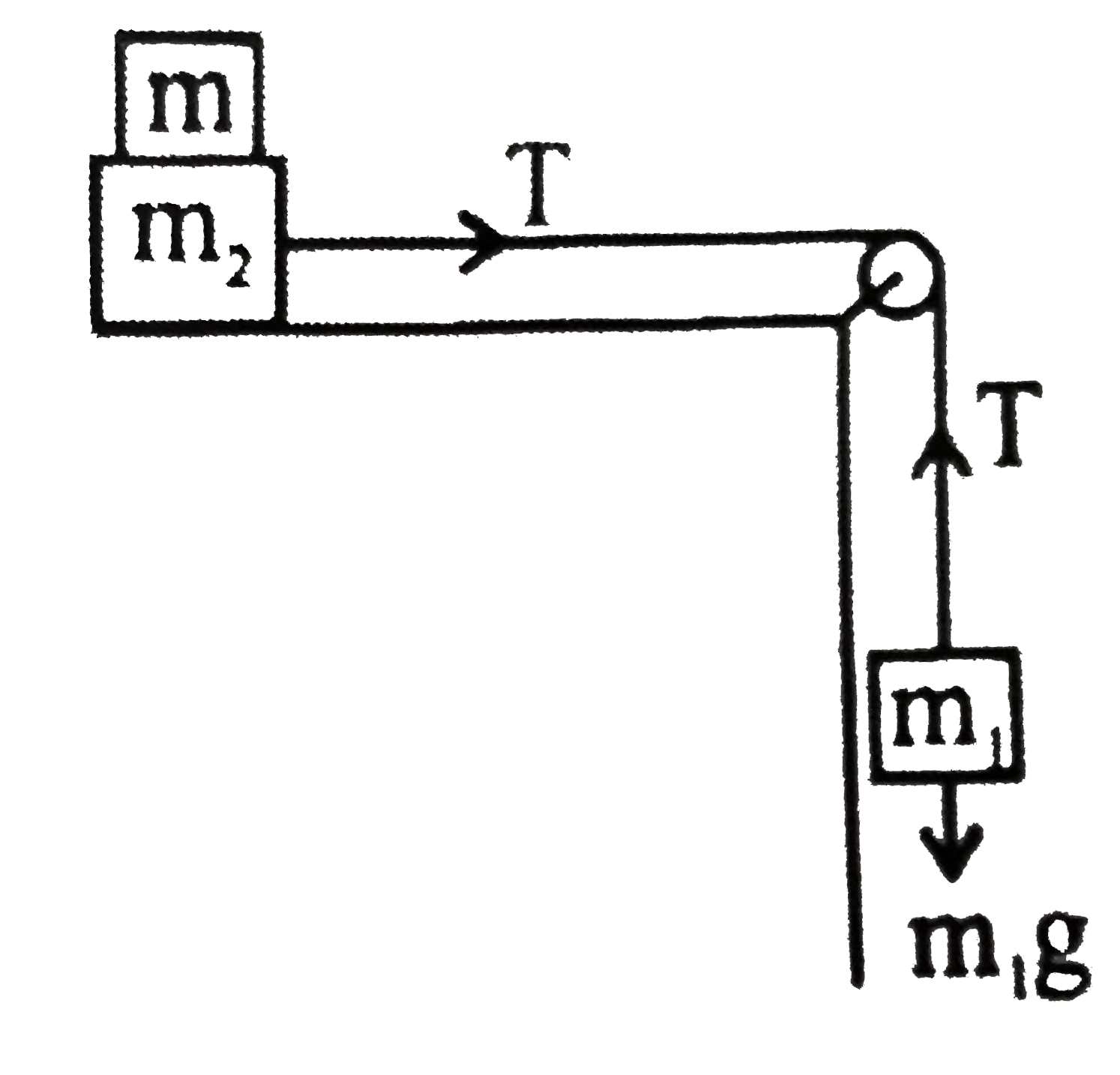
View SolutionTwo masses m1=5kgandm2=10kg, connected by an inextensible string over a frictionless pulley, are moving as shown in the figure. The coefficient of friction of horizontal surface is 0.15. The minimum weitght m that should be put on top of m2 to stop the motion is :-
View SolutionThe blocks ov mass m1=1kg and m2=2kg are connected by an ideal spring, rest on a rough horizontal surface. The spring is unstressed. The spring constant of spring is K=2N/m. The coefficient of friction between blocks and horizontal surface is μ=12. Now the left block is imparted a velocity u towards right as shown. The largest value of u( in m/s) such that the block of mass m2 never moves is ( Take g=10m/s2)
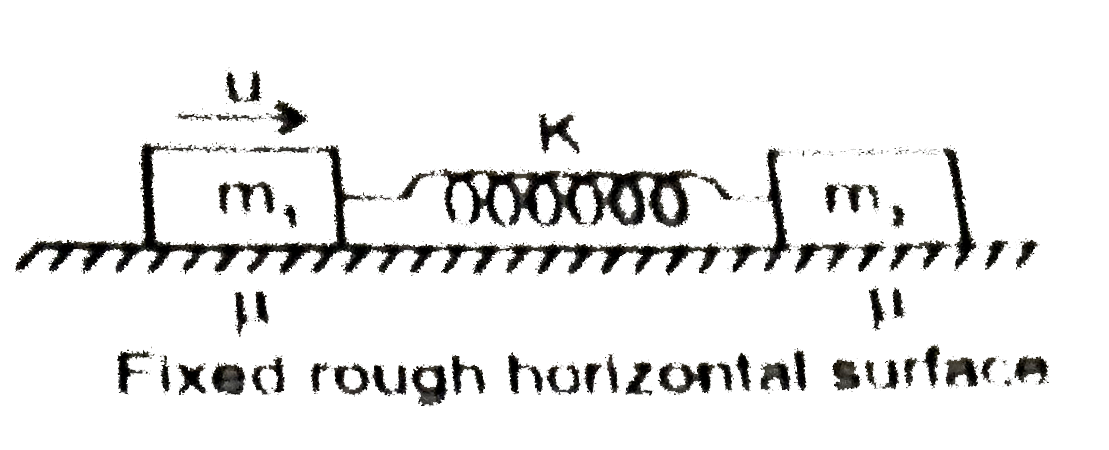
View SolutionA block of mass m is placed on another block of mass M lying on a smooth horizontal surface as shown in the figure. The co-efficient of friction between the blocks is μ. Find the maximum horizontal force F (in Newton) that can be applied to the block M so that the blocks together with same acceleration? (M=3kg,m=2kg,μ=0.1,g=10m/s2)

View SolutionA force of 200N is applied as shown in the figure on block of 3 kg. The coefficient of friction between the block and the wall is 0.3. Find the friction acting on the block. (in N) {Take g = 10 m/s2

View SolutionTwo blocks a and B of mass mA=1kg and mB=3kg are kept on the table as shown in figure the coefficient of friction between A and B is 0.2 and between B and the surface of the table is also 0.2 the maximum force F that can be applied on B horizontally, so that the block A does not slide over the block B is [Take g=10m/s2]
View Solution