Two blocks of masses $m_{1}$ and $m_{2}$ are connected by a spring of stiffness k. The coefficient of friction between the blocks and the surface is $μ$ . Find the minimum constant force F to be applied to $m_{1}$ in order to just slide the mass $m_{2}$ .

Video Solution

Text Solution

Verified by Experts

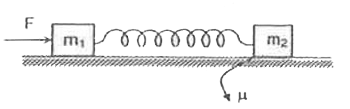
At any intermediate position the net external force is equal to
$F . = F - (μ m_{1} g + k x)$ (numerically)
$\Rightarrow$ The work done by the net external force F. in displacing the block $m_{1}$ through a length
$x_{0} = W_{ext} = \int F . . d x$
$\Rightarrow W_{ext} = \int_{0}^{x_{0}} {F - (μ m g + k x)} d x$
where $x_{0} =$ compression of the spring required to just move the block $m_{2}$ .
$\Rightarrow k x_{0} = μ m_{2} g$
$\Rightarrow x_{0} = \frac{μ m_{2} g}{k}$ .
Since the KE of the system just before moving the block $m_{1}$ & just before moving the block $m_{2}$ is zero, the change in $K E = 0$
$\Rightarrow Δ K E = 0$
$∴ W_{ext} = Δ K E$
$\Rightarrow \int_{0}^{x_{0}} F - (μ m_{1} g + k x) d x = 0$
$\Rightarrow F x_{0} - (μ m_{1} g x_{0} + \frac{k x_{0}^{2}}{2}) = 0$
$\Rightarrow F = μ m_{1} g + \frac{k x_{0}}{2} = μ m_{1} g + \frac{μ m_{2} g}{2} = [m_{1} + \frac{m_{2}}{2}] μ g$ .

|

Updated on:21/07/2023

Class 12 PHYSICS WORK, ENERGY AND POWER

Similar Questions

Recommended Questions

Home
Ask Doubt
Profile