In a region, potential energy varies with X as U(x)=30−(x−5)2 Joule, where x is in meters. A particle of mass 0.5 kg is projected from x=11 m towards origin with a velocity 'u' . u is the minimum velocity, so that the particle can reach the origin. (x=0). find the value of u/2 in meter/second. (Take √44=6.5)
To solve the problem, we need to determine the minimum velocity u required for a particle of mass 0.5kg to reach the origin (x = 0) when projected from x=11m. The potential energy U(x) is given by:
U(x)=30−(x−5)2J
Step 1: Determine the potential energy at the initial position (x = 11 m)
Substituting x=11 into the potential energy equation:
U(11)=30−(11−5)2
U(11)=30−(6)2
U(11)=30−36=−6J
Step 2: Determine the potential energy at the final position (x = 0 m)
Substituting x=0 into the potential energy equation:
U(0)=30−(0−5)2
U(0)=30−(5)2
U(0)=30−25=5J
Step 3: Apply the conservation of mechanical energy
The total mechanical energy at the initial position (x = 11 m) is the sum of kinetic energy and potential energy:
Einitial=K.E+U(11)=12mu2+U(11)
The total mechanical energy at the final position (x = 0 m) is:
Efinal=K.E+U(0)=0+U(0)=U(0)
Setting the initial and final energies equal gives us:
12mu2+U(11)=U(0)
Step 4: Substitute known values
Substituting m=0.5kg, U(11)=−6J, and U(0)=5J:
12(0.5)u2−6=5
0.25u2−6=5
0.25u2=5+6
0.25u2=11
Step 5: Solve for u2
Multiplying both sides by 4 to eliminate the fraction:
u2=44
Step 6: Solve for u
Taking the square root of both sides:
u=√44
Given that √44≈6.5:
Step 7: Find u2
Calculating u2:
u2=6.52=3.25m/s
Final Answer
Thus, the value of u2 is:
u2=3.25m/s
U(11)=30−(6)2
U(11)=30−36=−6J
U(0)=30−(5)2
U(0)=30−25=5J
0.25u2−6=5
0.25u2=5+6
0.25u2=11
Topper's Solved these Questions
Similar Questions
The potential energy of particle of mass 1kg moving along the x-axis is given by U(x)=16(x2−2x) J, where x is in meter. Its speed at x=1 m is2m/s. Then,
View SolutionLet gravitational potential energy U is given by U=A√xB+x2, where x is distance. The dimensional formula of A/B is
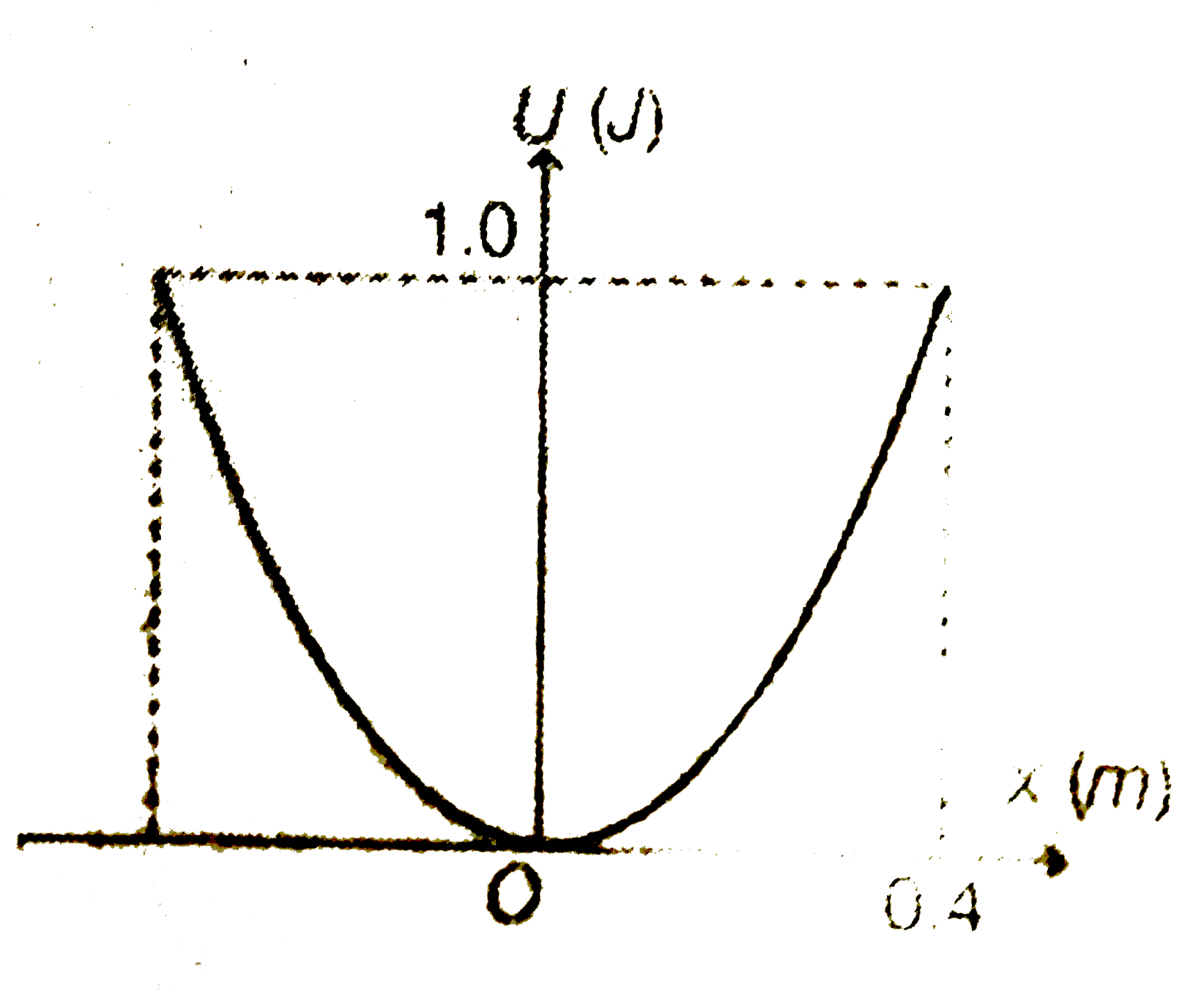
View SolutionA particle of mass = 2kg moves in simple harmonic motion and its potential energy U varies with position x as shown. The period of oscillation of the particle is nπ5 second. Find value of n.
View SolutionThe potential energy of a particle of mass 1 kg moving in X-Y plane is given by U=(12x+5y) joules, where x an y are in meters. If the particle is initially at rest at origin, then select incorrect alternative :-
View SolutionThe potential energy of a particle of mass 5 kg moving in the x−y plane is given by U=(−7x+24y)J, where x and y are given in metre. If the particle starts from rest, from the origin, then the speed of the particle at t=2s is
View SolutionThe potential energy of a particle of mass 5 kg moving in the x−y plane is given by U=(−7x+24y)J, where x and y are given in metre. If the particle starts from rest, from the origin, then the speed of the particle at t=2s is
View SolutionThe potential energy of a particle is given by formula U=100−5x+100x2,whereU and 'x' are in SI unit .if mass of particle is 0.1 Kg then find the magnitude of its acceleration
View SolutionA particle of mass 2kg moves in simple harmonic motion and its potential energy U varies with position x as shown. The period of oscillation of the particle is

View SolutionA particle of mass 2kg moves in simple harmonic motion and its potential energy U varies with position x as shown. The period of oscillation of the particle is

View SolutionA particle at origin (0,0) moving with initial velocity u=5msˆj and acceleration 10ˆi+4ˆj. After t time it reaches at position (20,y) then find t & y
View Solution