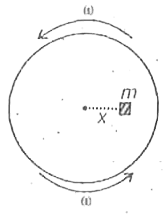
A cylinder of radius R is rotating about its horizontal axis with constant . A block of mass m is kept on
the inner surface of the cylinder. Block is moving in vertical circular motion without slipping. co–efficient of friction between block and surface of cylinder is . If minimum value of for complete vertical circular motion of block is then find 'x'.

so block does not leave circular motion
for limiting case
Topper's Solved these Questions
Similar Questions
A block of mass 10 kg is placed on the rough horizontal surface. A pulling force F is acting on the block which makes an angle θ above the horizontal. If coefficient of friction between block and surface is 43 then minimum value of force required to just move the block is (g=10ms2)
View SolutionA block of mass m is kept on horizontal turn table at x distance from the centre. If coefficient of friction between block and surface of turn table is μ, then maximum angular speed of the table so that block does not slip
View Solution
Knowledge Check
A block of mass m=2kg is resting on a rough inclined plane of inclination of 30∘ as shown in figure. The coefficient of friction between the block and the plane is μ=0.5. What minimum force F should be applied perpendicular to the plane on the block, so that blocks does not slip on the plane? (g=10m/s2)
 A2.68 NBZeroC4.34 ND6.24 N
A2.68 NBZeroC4.34 ND6.24 N
A block is kept on a rough horizontal surface as shown. Its mass is 2 kg and coefficient of friction between block and surface (μ)=0.5. A horizontal force F is acting on the block. When

View SolutionA block of mass m is pushed with a velocity v0 along the surface of a trolley car of mass M. If the horizontal ground is smooth and the coefficient of kinetic friction between the block of plank is μ. Find the minimum distance of relative sliding between the block and plank.

View SolutionA block of mass m is kept over another block of mass 2m. Coefficient of friction between two blocks is μ and that of between lower blood from the horizontal surface is zero. A horizontal force F=43μmg is applied on the block of mass 2m. Acceleration of lower block is
View SolutionFind the minimum value of horizontal force (F) required on the block of mass m to keep it at rest on the wall. Given the coefficient of friction between the surfaces is μ.
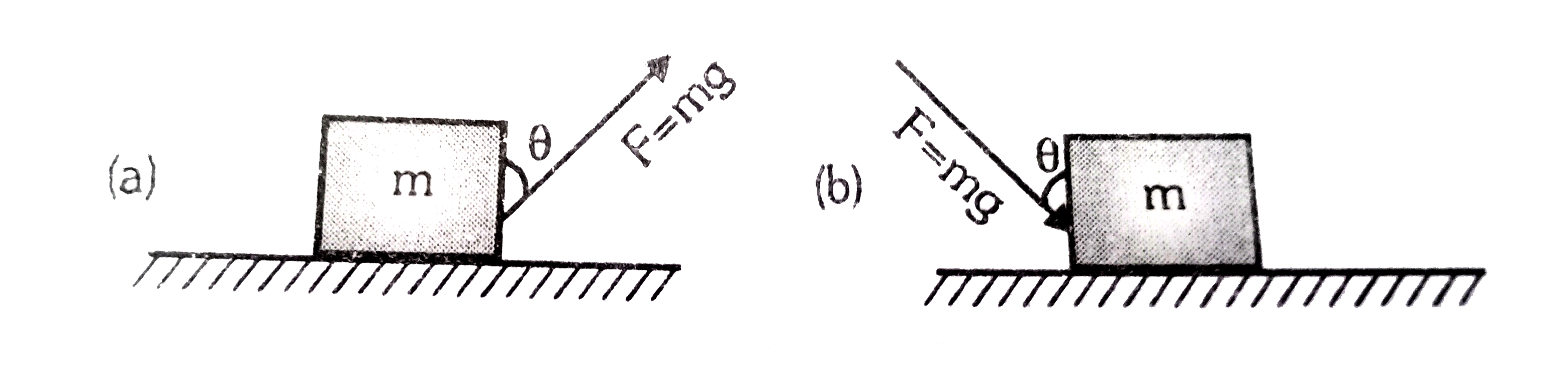
View SolutionA block of mass m rests on a rough horizontl surface as shown in figure (a) and (b). Coefficient of friciton between block and surface is μ. A force F-mg acting at an angle θ with the vertical side of the block. Find the condition for which block will move along the surface.
View SolutionA hemispherical bowl of radius R is rotated about its axis of symmetry which is kept vertical.A small block is kept in the bowl at a position where the radius makes an angle θ with the vertical. The block rotates with the bowl without any slipping. The friction coefficient between the block and the bowl surface is μ. Find the range of the angular speed for which the block will not slip.
View SolutionTwo block of masses m1 and m2 connected by a light spring rest on a horizontal plane. The coefficient of friction between the block and the surface is equal to μ. What minimum constant force has to be applied in the horizontal direction to the block of mass m1 in order to shift the other block?
View Solution
