Two blocks of mass m1 and m2 (m1<m2) are connected with an ideal spring on a smooth horizontal surface as shown in figure. At t = 0 m1 is at rest and m2 is given a velocity v towards right. At this moment, spring is in its natural length. Then choose the correct alternative :

Block of mass m2 will be finally at rest after some time.
Block of mass m2 will never come to rest.
Both the blocks will be finally at rest.
None of these
If velocity of m2 is zero then by momentum conservation m1v'=m2v
v'=m2vm1
Now, kinetic energy of m1
=12m1v'2=12m1(m2m1)2v2=12(m2m1)m2v2=(m2m1)12m2v2=m2m1× intial kinetic energy
Kinetic energy of m1> initial mechanical of system Henced proved
Topper's Solved these Questions
Similar Questions
Two blocks of masses m1 and m2 are connected by a massless spring and placed on smooth surface. The spring initially stretched and released. Then :
View SolutionTwo block of masses m1 and m2 are connected as shown in the figure. The acceleration of the block m2 is:

View Solution
Two blocks of masses m1 and m2 are connected as shown in the figure. The acceleration of the block m2 is :
View SolutionTwo smooth blocks of mases m1andm2 attached with an ideal spring of stiffness k and kept on hrozontal surface. If m1 is projected with a horizontal velocity v0. Find the maximum compression of the spring.
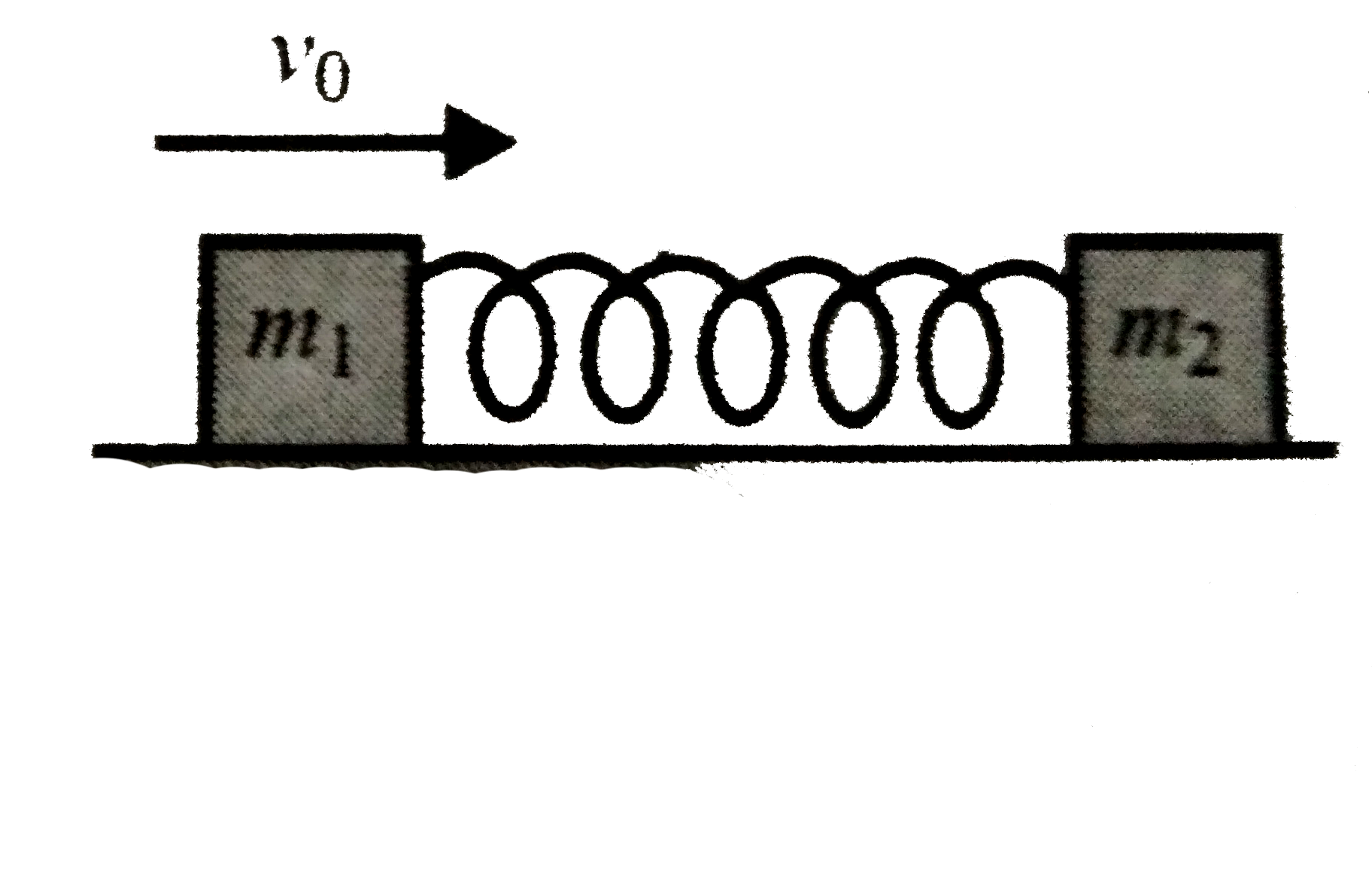
View SolutionTwo ring of mass m and 2m are connected with a light spring and can slide over two frictionless parallel horizontal rails as shown in figure. Ring of mass m is given velocity 'v0' in horizontal direction as shown. Calculate the maximum stretch in spring during subsequent motion.

View SolutionTwo blocks of masses m1andm2 are connected by a spring of spring constant k figure. The block of mass m2 is given a shape impulse so that it acquires a velocity v0 towards right. Find a. the velocity of the centre of mass b. the maximum elongation that the spring will suffer.
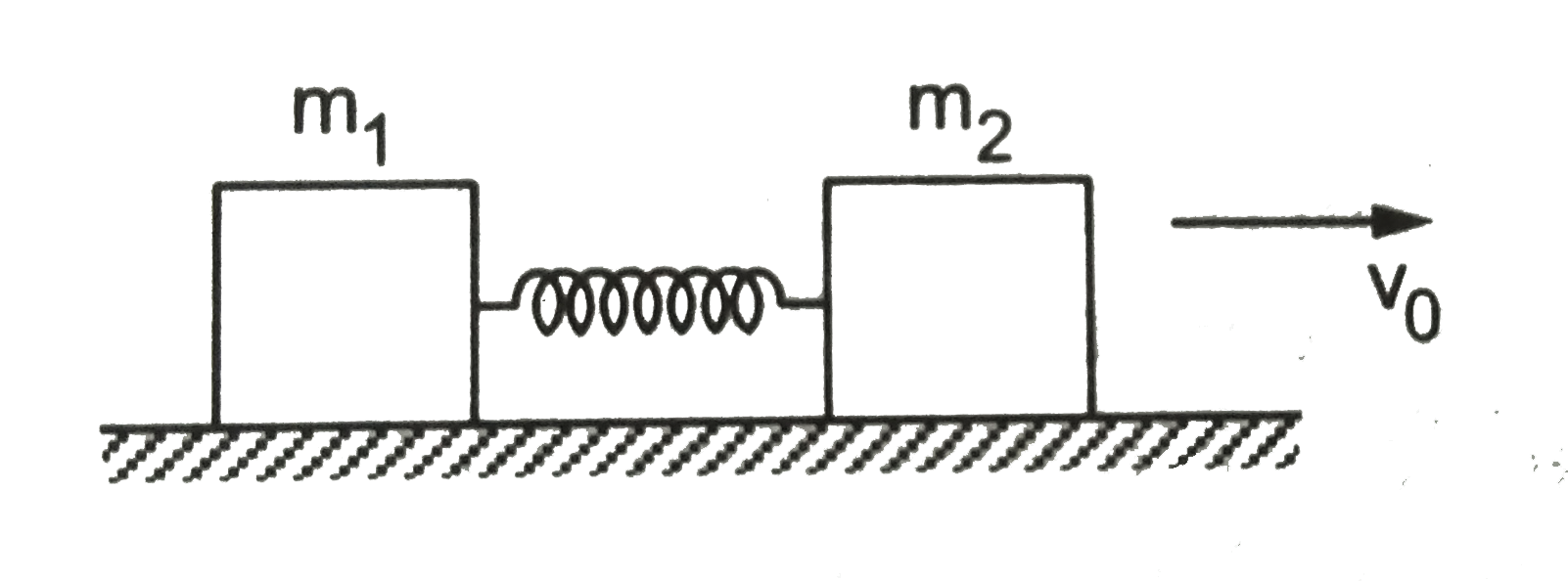
View SolutionTwo blocks of masses m1=1kg and m2 = 2kg are connected by a spring of spring constant k = 24 N/m and placed on a frictionless horizontal surface. The block m1 is imparted an initial velocity v0 = 12cm/s to the right. The amplitude of oscillation is
View SolutionTwo blocks of masses m1 and m2, connected by a weightless spring of stiffness k rest on a smooth horizontal plane as shown in Fig. Block 2 is shifted a small distance x to the left and then released. Find the velocity of centre of mass of the system after block 1 breaks off the wall.

View SolutionTwo blocks A and B of mass m and 2m respectively are connected by a light spring of force constant k. They are placed on a smooth horizontal surface. Spring is stretched by a length x and then released. Find the relative velocity of the blocks when the spring comes to its natural length

View SolutionTwo blocks A and B of masses in and 2m, respectively, are connected with the help of a spring having spring constant, k as shown in Fig. Initially, both the blocks arc moving with same velocity v on a smooth horizontal plane with the spring in its natural length. During their course of motion, block B makes an inelastic collision with block C of mass m which is initially at rest. The coefficient of restitution for the collision is 1/2. The maximum compression in the spring is
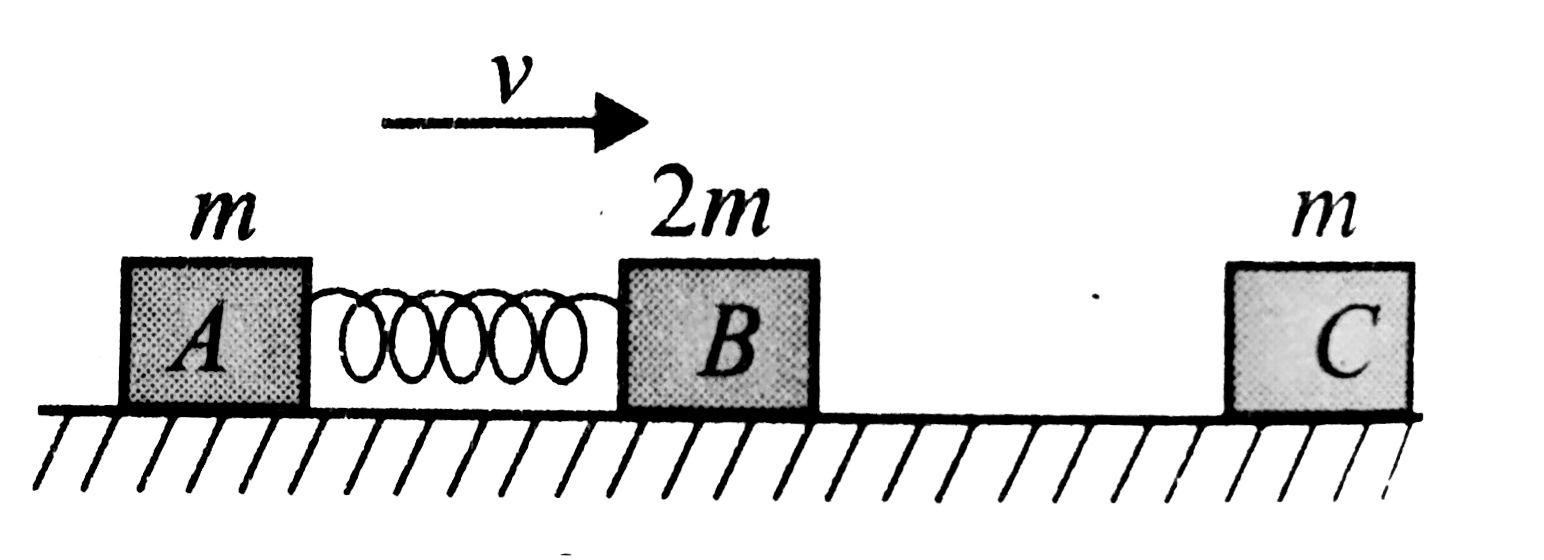
View Solution

