Two blocks of masses m1andm2 are connected by a spring of spring constant k figure. The block of mass m2 is given a shape impulse so that it acquires a velocity v0 towards right. Find a. the velocity of the centre of mass b. the maximum elongation that the spring will suffer.
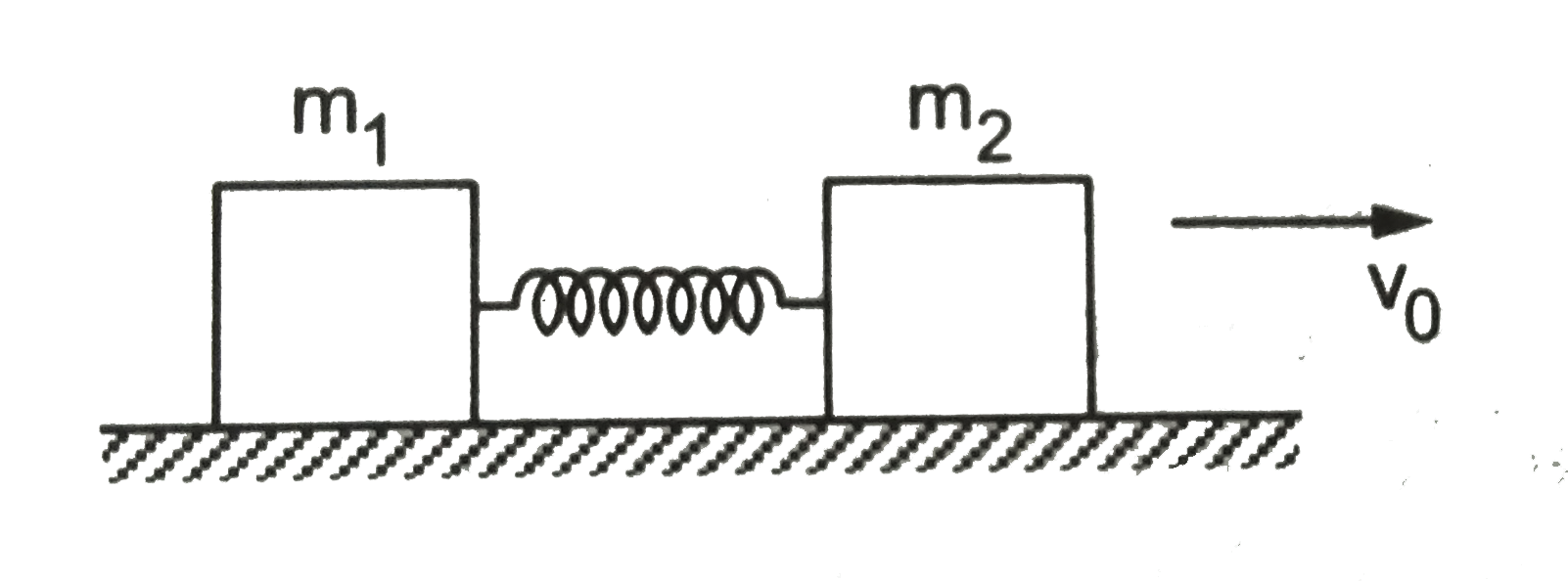
Velocity of centre of mass
=m1v1+m2v2m1+m2
Hence v1=0,v2=v0
=m1×0+m2×v0m1+m−2
=m2v0m1+m2
b. The spring wil attain maximum elongation when both velocities of two blocks wil attain are veolicy of centre of mass.
x→maxiμmelongationofspr∈g<br>chan≥∈k∈etice≠rgy<br>=potentiale≠rgys→red∈spr∈g<br>rarr 1/2 m_2v_2^2-1/2(m_1+m_2)((m_2v_0)/(m_1+m_2))^2<br>=1/2kx^2<br>rarr m_2v_0^2(1-m^2/(m_1+m_2)=kx^2<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/HCV_VOL1_C09_E01_104_S01.pngwh=80%mx-autosty≤=background:white;><br>rarr x=[(m_1m_2)/(m_1+m_2)]^91/2)V_0
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBook:HC VERMA ENGLISHChapter:CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONExercise:Question For short Answer
Explore 25 Videos
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBook:HC VERMA ENGLISHChapter:CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONExercise:Objective -2
Explore 11 Videos
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBook:HC VERMA ENGLISHChapter:CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONExercise:Objective -1
Explore 18 Videos
- CALORIMETRYBook:HC VERMA ENGLISHChapter:CALORIMETRYExercise:Short answer
Explore 9 Videos
- CIRCULAR MOTIONBook:HC VERMA ENGLISHChapter:CIRCULAR MOTIONExercise:Question for short Answer
Explore 10 Videos
Similar Questions
A block of mass m is suspended by different springs of force constant shown in figure.

View SolutionA block of mass m suspended from a spring of spring constant k. Find the amplitude of S.H.M.
View SolutionTwo blocks of masses m1 and m2 are connected by a massless spring and placed on smooth surface. The spring initially stretched and released. Then :
View SolutionTwo blocks of masses m1=1kg and m2 = 2kg are connected by a spring of spring constant k = 24 N/m and placed on a frictionless horizontal surface. The block m1 is imparted an initial velocity v0 = 12cm/s to the right. The amplitude of oscillation is
View SolutionA block of mass m is connected to a spring of spring constant k as shown in figure. The frame in which the block is placed is given an acceleration a towards left. Neglect friction between the block and the frame walls. The maximum velocity of the block relative to the frame is

View SolutionTwo blocks of masses 5kg and 2kg are connected by a spring of negligible mass and placed on a frictionless horizontal surface. An impulse provides a velocity of 7m/s to the heavier block in the direction of the lighter block. The velocity of the centre of mass is :-
View SolutionTwo blocks of masses 5kg and 2kg are connected by a spring of negligible mass and placed on a frictionless horizontal surface. An impulse provides a velocity of 7m/s to the heavier block in the direction of the lighter block. The velocity of the centre of mass is :-
View SolutionTwo blocks of masses 5kg and 2kg are connected by a spring of negligible mass and placed on a frictionless horizontal surface. An impulse provides a velocity of 7m/s to the heavier block in the direction of the lighter block. The velocity of the centre of mass is :-
View SolutionTwo blocks of masses m and m' are connected by a light spring on a horizontal frictionless table . The spring is compressed and then released . Find the ratio of acceleration of masses .
View SolutionTwo blocks of masses m1 and m2, connected by a weightless spring of stiffness k rest on a smooth horizontal plane as shown in Fig. Block 2 is shifted a small distance x to the left and then released. Find the velocity of centre of mass of the system after block 1 breaks off the wall.

View Solution