A particle of mass 1×10−26kg and charge +1.6×10−19C travelling with a velocity 1.28×106ms−1 in the +x direction enters a region in which uniform electric field E and a uniform magnetic field of induction B are present such that Ex=Ey=0,Ez=−102.4kVm−1,andBx=Bz=0,By=8×10−2. The particle enters this region at time t=0. Determine the location (x,y,z coordinates) of the particle at t=5×10−6s. If the electric field is switched off at this instant (with the magnetic field present), what will be the position of the particle at t=7.45×10−6s ?
The Lorentz force on the charged particle is
F=q(→E+→v×→B).
The electric force on the charged particle, FE=qEz which acts
towards negative z direction.

The magnetic force on the charged particle, FB=qvxBy.
As velocity of charge is in +x direction and magnetic field is
along +y direction, from right hand rule the magnetic force acts
along +z direction. The resultant force,
F=FE+FB=q(Ez+vxBy)
=q[−102.4×103+1.28×106×8×10−2]=0
During time t=0 to t1=5×10−6, the resultant force on the
particle is zero, it moves with uniform velocity vx. The position
of the particle (X1,Y1,Z1) after time t1 is
X1=vxt1=(1.28×106)×(5×10−6)=6.4m
When electric field is switched off, the particle circulates in xz-
plane under the influence of magnitude field.
Radius R of circulation is
R=mvxqBy=10−26×1.28×1061.6×10−19×8×10−2=1m
θ=P1P2R=vx(t2−t1)R=(1.28×106)×2.45×10−61
=3.136=πradian
The coordinates of the particle are
X2=X1+Rsinθ=X1+Rsinπ=X1=16.4m
and Z2=R−Rcosθ=R−Rcosπ=2R=2m
Note that θ=π implies that t2=T/2, where T is time period of
circulation. We could have written the result directly.
Topper's Solved these Questions
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercise 1.1
22 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercise 1.2
13 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type
2 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Concept Based
8 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False
3 Videos
Similar Questions
A particle of mass 2×10−3 kg, charge 4×10−3C enters in an electric field of 5V/m, then its kinetic energy after 10 s is
View SolutionA charge particle travels along a straight line with a speed v in region where both electric field E and magnetic field b are present.It follows that
View SolutionA proton of mass 1.67×10−27 kg and charge 1.6×10−19C is shot a uniform magnetic field, and perpendicular to the field with a velocity 5×106m/s. If the magnetic induction of the field is 1 tesla, find
(i) The radius of the circular path
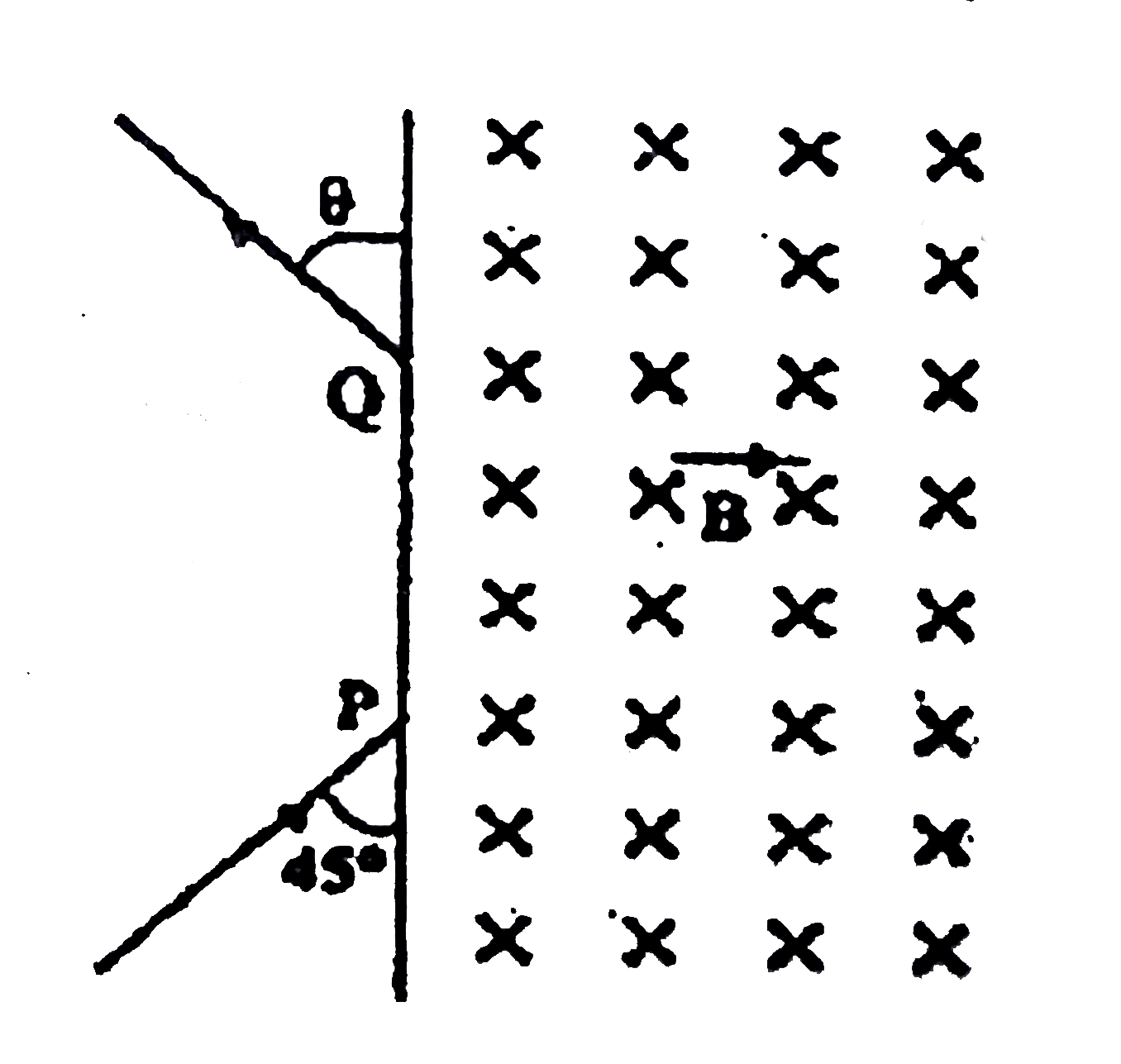
View SolutionA particle of mass 1.6×10−27kg and charge 1.6×10−19 coulomb enters a uniform magnetic field of 1 Tesla as shown in the figure. The speed of the particle is 107m/s. The distance PQ will be
View SolutionA particle of mass m=1.6X10−27 kg and charge q=1.6X10−19 C moves at a speed of 1.0X107ms−7. It enters a region of uniform magnetic field at a point E, as shown in The field has a strength of 1.0 T. (a) The magnetic field is directed into the plane of the paper. The particle leaves the region of the filed at the point F. Find the distance EF and the angle theta. (b) If the field is coming out of the paper, find the time spent by the particle in the regio the magnetic feld after entering it at E.

View SolutionA particle of mass 0.6g and having charge of 25nC is moving horizontally with a uniform velocity 1.2×104ms−1 in a uniform magnetic field, then the value of the magnetic induction is (g=10ms−2)
View SolutionA particle of mass 0.6g and having charge of 25nC is moving horizontally with a uniform velocity 1.2×104ms−1 in a uniform magnetic field, then the value of the magnetic induction is (g=10ms−2)
View SolutionIn a certain region, uniform electric field E=−E0ˆk and magnetic field B=B0ˆk are present. At time t=0, a particle of mass m and charge q is given a velocity v=vj+vk. Find the minimum speed of the particle and the time when it happens so.

View SolutionA particle of mass m and charge Q moving with a velocity v enters a region on uniform field of induction B Then its path in the region is s
View SolutionA particle of charge −16×10−18 coulomb moving with velocity 10ms−1 along the x− axis , and an electric field of magnitude 104/(m) is along the negative z− axis. If the charged particle continues moving along the x- axis , the magnitude of B is
View Solution

