A small charged ball having mass m and charge q is suspended from a rigid support by means of an inextensible thread of length l. It is made to rotate on a horizontal circular path in a uniform, time independent magnetic field of induction B which is directed upward. The time period of revolution of the ball is T0. If the thread is always stretched, calculate the radius of circular path on which the ball moves.
To solve the problem step by step, we will analyze the forces acting on the charged ball and derive the radius of the circular path it follows.
Step 1: Understand the forces acting on the ball
The ball is subjected to three main forces:
1. The gravitational force acting downward: Fg=mg
2. The tension in the thread acting along the thread: T
3. The magnetic force acting perpendicular to the velocity of the ball: Fm=qvB
Step 2: Set up the equations of motion
Since the ball is moving in a circular path, we can resolve the tension T into two components:
- The vertical component: Tcosθ=mg (1)
- The horizontal component: Tsinθ=mv2r+qvB (2)
Where:
- θ is the angle between the thread and the vertical.
- v is the linear velocity of the ball.
- r is the radius of the circular path.
Step 3: Relate linear velocity to angular velocity
The linear velocity v can be expressed in terms of the angular velocity ω and the radius r:
v=rω
Step 4: Substitute v into the equations
Substituting v=rω into equation (2):
Tsinθ=m(rω)2r+q(rω)B
This simplifies to:
Tsinθ=mrω2+qBrω
Step 5: Express T in terms of θ
From equation (1), we can express T:
T=mgcosθ
Step 6: Substitute T into the horizontal force equation
Now substitute T into the horizontal force equation:
mgcosθsinθ=mrω2+qBrω
This simplifies to:
mgtanθ=mrω2+qBrω
Step 7: Relate tanθ to r and l
Using the geometry of the problem, we have:
tanθ=r√l2−r2
Thus:
mgr√l2−r2=mrω2+qBrω
Step 8: Isolate r
Rearranging gives:
mgr=√l2−r2(mrω2+qBrω)
Squaring both sides and simplifying will lead to an equation in terms of r.
Step 9: Solve for r
After simplification, we can express r in terms of known quantities m,g,q,B,T0,l.
Final Expression
The final expression for the radius r will be derived from the above steps, leading to:
r=
⎷l2−(T204π2(gT0+qBmg))
The ball is subjected to three main forces:
1. The gravitational force acting downward: Fg=mg
2. The tension in the thread acting along the thread: T
3. The magnetic force acting perpendicular to the velocity of the ball: Fm=qvB
Since the ball is moving in a circular path, we can resolve the tension T into two components:
- The vertical component: Tcosθ=mg (1)
- The horizontal component: Tsinθ=mv2r+qvB (2)
- θ is the angle between the thread and the vertical.
- v is the linear velocity of the ball.
- r is the radius of the circular path.
The linear velocity v can be expressed in terms of the angular velocity ω and the radius r:
v=rω
Substituting v=rω into equation (2):
Tsinθ=m(rω)2r+q(rω)B
This simplifies to:
Tsinθ=mrω2+qBrω
From equation (1), we can express T:
T=mgcosθ
Now substitute T into the horizontal force equation:
mgcosθsinθ=mrω2+qBrω
This simplifies to:
mgtanθ=mrω2+qBrω
Using the geometry of the problem, we have:
tanθ=r√l2−r2
Thus:
mgr√l2−r2=mrω2+qBrω
Rearranging gives:
mgr=√l2−r2(mrω2+qBrω)
Squaring both sides and simplifying will lead to an equation in terms of r.
After simplification, we can express r in terms of known quantities m,g,q,B,T0,l.
The final expression for the radius r will be derived from the above steps, leading to:
r=
⎷l2−(T204π2(gT0+qBmg))
Topper's Solved these Questions
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercise 1.1
22 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercise 1.2
13 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type
2 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Concept Based
8 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False
3 Videos
Similar Questions
A charged particle moves in a circular path in a uniform magnetic field. If its speed is reduced, then its tiem period will
View SolutionA charged particle is moving in a circular path in uniform magnetic field. Match the following.

View SolutionA particle of mass 'm' and charge 'q' is suspended from the ceiling with the help of an insulating wire of length 'l'. It is placed in an uniform electric field as shown in figure. Then the time period of oscillation is
_2019_CBT6_E01_041_Q01.png)
View SolutionThe time period of a charged particle undergoing a circular motion in a uniform magnetic field is independent of its
View SolutionA charge particle is moving in a uniform magnetic field ib a circular path. The energy of the particle is doubled . If the initial radius of he circular path was R, the radius of the new circular path after the energy is doubled will be
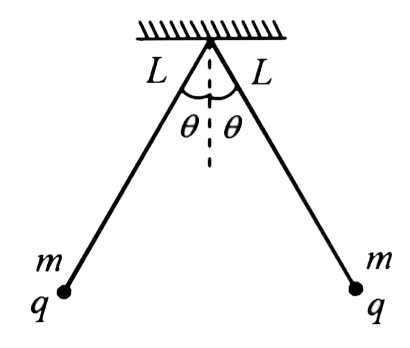
View SolutionTwo small spheres each of mass m and charge q are tied from the same rigid support with the help of silk threads of length L. They make angle θ with the vertical as shown in the fig. If length L is decreased, then angle θ with the vertical.
View SolutionA small ball of mass m and charge q is attached to the bottom end of a piece of negligible mass thread of length l, whose top end is fixed. The system formed by the thread and ball is in vertical plane and is in uniform horizontal magnetic field B, which is perpendicular to the plane of figure and points into the paper

The ball is started with a velocity v0 from lower most point of circle in a direction perpendicular both to the magnetic induction and to direction of thread. The ball moves along a circular path such that thread remains tight during the whole motion. Neglect any loss of enery.
Choose CORRECT statement
View SolutionA small ball of mass m and charge q is attached to the bottom end of a piece of negligible mass thread of length l, whose top end is fixed. The system formed by the thread and ball is in vertical plane and is in uniform horizontal magnetic field B, which is perpendicular to the plane of figure and points into the paper

The ball is started with a velocity v0 from lower most point of circle in a direction perpendicular both to the magnetic induction and to direction of thread. The ball moves along a circular path such that thread remains tight during the whole motion. Neglect any loss of enery.
What is the magnitude of magnetic induction B, if the minimum initial speed at which the described motion of ball (complete vertical circular motion) occurs is V0=12√17gL
View SolutionA charged particle of mass m and charge q describes circular motion of radius r in a uniform magnetic field of strength B the frequency of revolution is
View SolutionA charged particle of mass m and charge q is accelerated through a potential differences of V volts. It enters of uniform magnetic field B which is directed perpendicular to the direction of motion of the particle. The particle will move on a circular path of radius
View Solution
